Работа с графикой: визуализация функций двух переменных
7.4. Визуализация функций трёх переменных в трёхмерном пространстве
В предыдущем разделе мы научились представлять функциональные зависимости и дискретные наборы данных от двух переменных на плоскости, заменяя третью координату цветом (изображение плотности функции) или линиями уровня (контурное изображение). Похожий трюк мы используем для представления в трёхмерном пространстве зависимостей от трёх переменных, для которых принципиально нет возможности снабдить и функцию, и каждую переменную собственной координатной осью. В этом нам поможет функция ContourPlot3D. Заданная в виде ContourPlot3D[{f,{x,xmin,xmax},{y,ymin,ymax},{z,zmin,zmax}}] функция генерирует трёхмерное контурное изображение функции f переменных x, y и z, при этом, в отличие от двумерного случая, контурами будут являться криволинейные поверхности. Функция ContourPlot3D[{f==g,{x,xmin,xmax},{y,ymin,ymax},{z,zmin,zmax}}] рисует только ту контурную поверхность, для которой f и g равны.
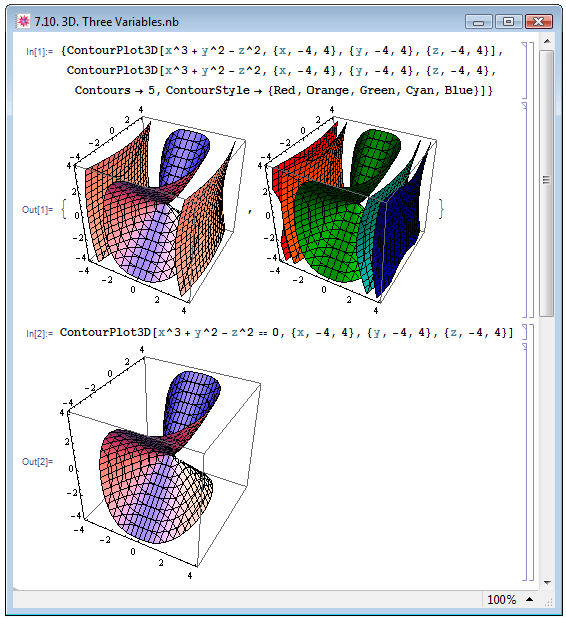
В примере In[1] на рис. 7.10 мы построили в контурном представлении некоторую зависимость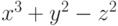 
. На рисунке слева мы обошлись без дополнительных настроек. Поскольку количеством контуров и их оформлением в трёхмерном случае можно манипулировать точно так же, как и в двумерном, на рисунке справа мы построили на рисунке пять контуров, Contours->5/, характеризующих зависимость, и каждый из них раскрасили в определённый цвет, ContourStyle->{Red,Orange,Green,Cyan,Blue}.
В примере In[2] на рис. 7.10 мы построили контурную поверхность той же зависимости, удовлетворяющую условию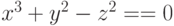 
.
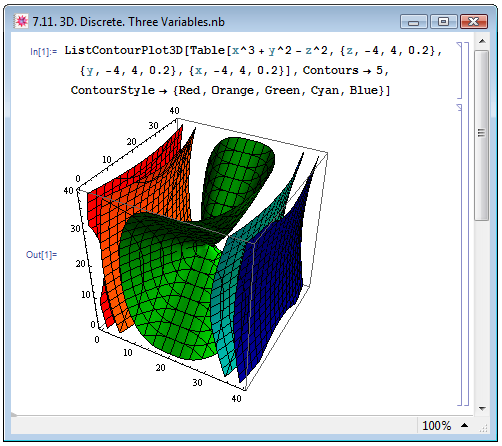
Имеется в Mathematica и функция для представления в трёхмерном пространстве дискретного набора данных по трём координатам — ListContourPlot3D. В качестве аргумента выступает трёхуровневый вложенный список, т. о., функция задаётся в виде ListContourPlot3D[{{{f111,f112,...},{f121,f122,...},...},{{f211,f212,...},{f221,f222,...},...},...}], где индексы в виде ijk нумеруют элемент списка со значением функции fijk. На рисунке 7.11 мы построили ту же зависимость, что и в примере In[1] на рис. 7.10, однако задали её в дискретном виде при помощи функции Table.
Специальных функций для плотностной визуализации зависимостей от трёх переменных в Mathematica нет.
Подробней о трёхмерных функциях визуализации зависимостей от трёх переменных см. книгу В. П. Дьяконова [2, с. 468–470].
7.5. Трёхмерные графические примитивы
Примитивы двумерной графики, точка, линия, прямоугольник, многоугольник, дуга, диск, текст, используются также и для построения трёхмерных графических изображений. Единственное отличие в трёхмерном случае заключается в том, что позиции всех точек описываются не двумя, а тремя координатами.
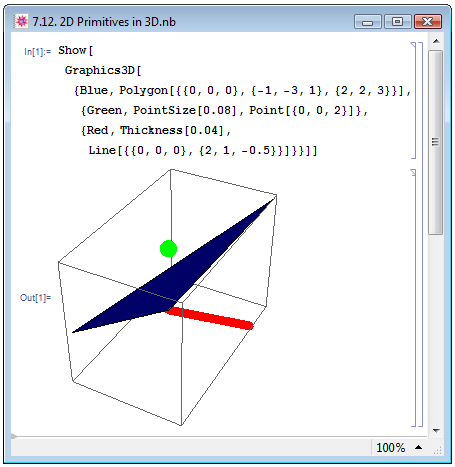
Для того чтобы превратить в рисунок трёхмерные примитивы, к ним следует применить функцию Graphics3D. На рис. 7.12 мы изобразили в трёхмерном пространстве точку, линию и многоугольник (треугольник). Для того чтобы отличать трёхмерное изображение от двумерного Mathematica заключила изображение в коробку.
Однако трёхмерная графика обладает собственными специфическими примитивами, представляющими собой трёхмерные минимальные объекты: это параллелепипед (cuboid), сфера (sphere), цилиндр (cylinder), конус (cone), труба (tube).
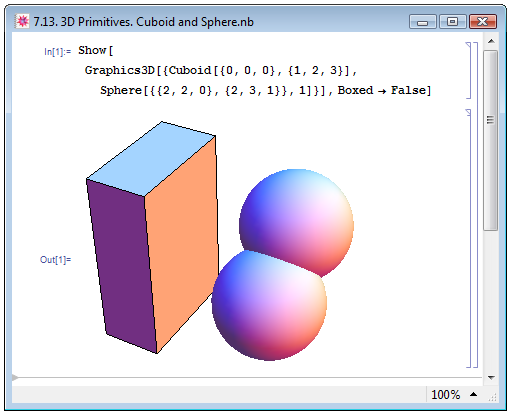
Примитив Cuboid[{xmin,ymin,zmin},{xmax,ymax,zmax}] рисует параллелепипед, стороны которого параллельны координатным осям, а противоположные углы на одной из диагоналей имеют координаты {xmin.ymin,zmin} и {xmax,ymax,zmax}.
Примитив Sphere[{x,y,z},r] изображает сферу радиуса r с центром в точке с координатами {x,y,z}.
На рис. 7.13 мы изобразили при помощи соответствующих примитивов параллелепипед и две пересекающихся сферы. Кроме того, мы воспользовались уже известной нам опцией Boxed для того, чтобы убрать обрамляющую изображение "коробку". Следует отметить, что эту опцию мы указали вне списка, содержащего графические примитивы и директивы, а как отдельный аргумент функции Graphics3D.
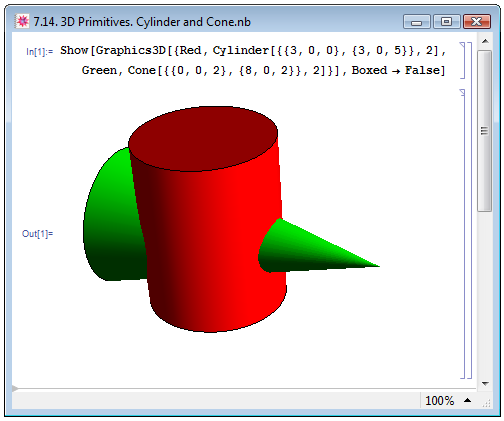
Примитивы Cylinder[{{x1,y1,z1},{x2,y2,z2}},r] и Cone[{{x1,y1,z1},{x2,y2,z2}},r] рисуют соответственно цилиндр и конус с радиусами оснований r, осями которых выступает линия с координатами {x1,y1,z1},{x2,y2,z2}. Эффект использования обоих примитивов проиллюстрирован на рис. 7.14.
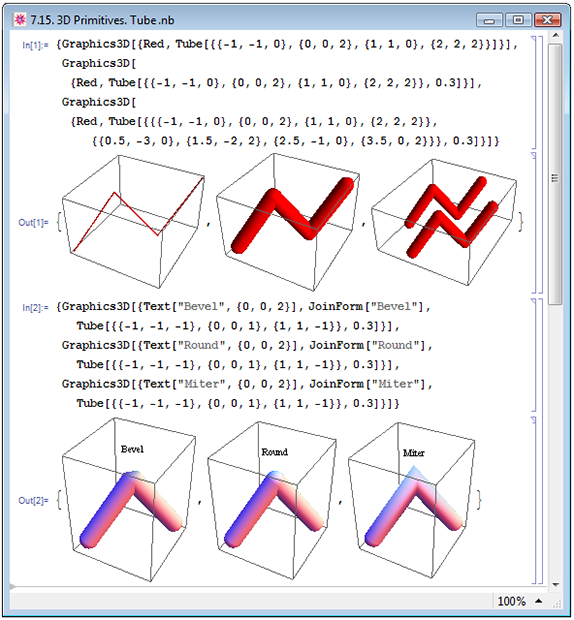
Примитив Tube рисует в трёхмерном пространстве тело, которое мы будем называть трубой: это трёхмерный объект, представляющий собой некоторую суперпозицию линии и цилиндра. Заданный в виде Tube[{{x(1),y(1),z(1)},{x(2),y(2),z(2)},...}] примитив рисует цилиндры вокруг линий, соединяющих точки с заданными координатами {x(i),y(i),z(i)},{x(i+1),y(i+1),z(i+1)} (левое изображение в Out[1] на рис. 7.15). Если задать функцию с дополнительным аргументом, Tube[{{x(1),y(1),z(1)},{x(2),y(2),z(2)},...},r], то рисуются цилиндры радиуса r (центральное изображение в Out[1]). Если мы обратим внимание на открытые концы изображённых при помощи Tube тел, то увидим, что они не плоские, как у цилиндра, а скруглённые.
При помощи примитива Tube можно одновременно создавать изображение нескольких труб, задав в качестве первого аргумента список описывающих их линий (правое изображение в Out[1] на рис. 7.15). Можно менять способ соединения цилиндров соседних отрезков линии. Для этого используется директива JoinForm. Существует три способа соединения: скос (Bevel), скругление (Round) и угол (Miter). Все способы представлены в примере In[2].
Подробней о двумерных и трёхмерных графических примитивах Mathematica — в книге Ш. Гетца и Дж. Хелмстедт [9, с. 28–35, 49–52].
