Обучение с учителем: Распознавание образов
Адаптивная оптимизации архитектуры сети
Итак, мы выяснили, что существует оптимальная сложность сети, зависящая от количества примеров, и даже получили оценку размеров скрытого слоя для двухслойных сетей. Однако в общем случае следует опираться не на грубые оценки, а на более надежные механизмы адаптации сложности нейросетевых моделей к данным для каждой конкретной задачи.
Для борьбы с переобучением в нейрокомпьютинге используются три основных подхода:
- Ранняя остановка обучения
- Прореживание связей (метод от большого - к малому)
- Поэтапное наращивание сети (от малого - к большому)
Валидация обучения
Прежде всего, для любого из перечисленных методов необходимо определить критерий оптимальной сложности сети - эмпирический метод оценки ошибки обобщения. Поскольку ошибка обобщения определена для данных, которые не входят в обучающее множество, очевидным решением проблемы служит разделение всех имеющихся в нашем распоряжении данных на два множества: обучающее - на котором подбираются конкретные значения весов, и валидационного - на котором оценивается предсказательные способности сети и выбирается оптимальная сложность модели. На самом деле, должно быть еще и третье - тестовое множество, которое вообще не влияет на обучение и используется лишь для оценки предсказательных возможностей уже обученной сети.
Ранняя остановка обучения
Обучение сетей обычно начинается с малых случайных значений весов. Пока значения весов малы по сравнением с характерным масштабом нелинейной функции активации (обычно принимаемом равным единице), вся сеть представляет из себя суперпозицию линейных преобразований, т.е. является также линейным преобразованием с эффективным числом параметров равным числу входов, умноженному на число выходов. По мере возрастания весов и степень нелинейности, а вместе с ней и эффективное число параметров возрастает, пока не сравняется с общим числом весов в сети.
В методе ранней остановки обучение прекращается в момент, когда сложность сети достигнет оптимального значения. Этот момент оценивается по поведению во времени ошибки валидации. Рисунок 3.8. дает качественное представление об этой методике.
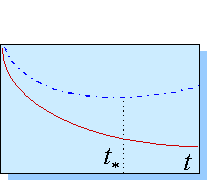
Рис. 3.8. Ранняя остановка сети в момент минимума ошибки валидации (штрих-пунктирная кривая). При этом обычно ошибка обучения (сплошная кривая) продолжает понижаться
Эта методика привлекательна своей простотой. Но она имеет и свои слабые стороны: слишком большая сеть будет останавливать свое обучение на ранних стадиях, когда нелинейности еще не успели проявиться в полную силу. Т.е. эта методика чревата нахождением слабо-нелинейных решений. На поиск сильно нелинейных решений нацелен метод прореживания весов, который, в отличае от предыдущего, эффективно подавляет именно малые значения весов.
Прореживание связей
Эта методика стремится сократить разнообразие возможных конфигураций обученных нейросетей при минимальной потере их аппроксимирующих способностей. Для этого вместо колоколообразной формы априорной функции распределения весов, характерной для обычного обучения, когда веса "расползаются" из начала координат, применяется такой алгоритм обучения, при котором функция распределения весов сосредоточена в основном в "нелинейной" области относительно больших значений весов (см. рисунок 3.9).
Этого достигают введением соответствующей штрафной составляющей в функционал ошибки. Например, априорной функции распределения:
![P(N)\infty\exp\left[-\lambda\sum_{ij}\frac{w^{2}_{ij}}{w^2_0+w^2_{ij}}\right],](/sites/default/files/tex_cache/d21e91185dc45a0537e2c0a49404f655.png)
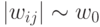, соответствует штрафной член: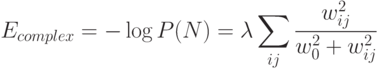
, и пропорциональна величине малых весов, 
. Соответственно, на больших штрафная функция практически
не сказывается, тогда как малые веса экспоненциально затухают.Таким образом, происходит эффективное вымывание малых весов (weights elimination), т.е. прореживание малозначимых связей. Противоположная методика предполагает, напротив, поэтапное наращивание сложности сети. Соответствующее семейство алгоритмов обучения называют конструктивными алгоритмами.
Конструктивные алгоритмы
Эти алгоритмы характеризуются относительно быстрым темпом обучения, поскольку разделяют сложную задачу обучения большой многослойной сети на ряд более простых задач, обычно - обучения однослойных подсетей, составляющих большую сеть. Поскольку сложность обучения пропорциональна квадрату числа весов, обучение "по частям" выгоднее, чем обучение целого:
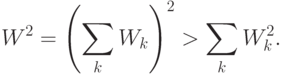
Для примера опишем так называемую каскад-корреляционную методику обучения нейросетей. Конструирование сети начинается с единственного выходного нейрона и происходит путем добавления каждый раз по одному промежуточному нейрону (см. рисунок 3.10).
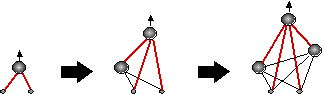
Рис. 3.10. Каскад-корреляционные сети: добавление промежуточных нейронов с фиксированными весами (тонкие линии)
Эти промежуточные нейроны имеют фиксированные веса, выбираемые таким образом, чтобы выход добавляемых нейронов в максимальной степени коррелировал с ошибками сети на данный момент (откуда и название таких сетей). Поскольку веса промежуточных нейронов после добавления не меняются, их выходы для каждого значения входов можно вычислить лишь однажды. Таким образом, каждый добавляемый нейрон можно трактовать как дополнительный признак входной информации, максимально полезный для уменьшения ошибки обучения на данном этапе роста сети. Оптимальная сложность сети может определяться, например, с помощью валидационного множества.