Обучение с учителем: Распознавание образов
Английской грамматикой в объеме Basic English первым овладел Proteus orator mirabilis, тогда как E.coli eloquentissima даже в 21 000 поколении делал, увы, грамматические ошибки. С.Лем, "Эрунтика"
постарайся, насколько можешь отвечать о чем я буду спрашивать тебя. И, если я по рассмотрении твоего ответа найду в нем нечто призрачное и неистинное, незаметно выну это и отброшу
Платон, " Теэтет"
Персептроны. Прототипы задач
Сети, о которых пойдет речь в этой лекции, являются основной "рабочей лошадкой" современного нейрокомпьютинга. Подавляющее большинство приложений связано именно с применением таких многослойных персептронов или для краткости просто персептронов (напомним, что это название происходит от английского perception - восприятие, т.к. первый образец такого рода машин предназначался как раз для моделирования зрения). Как правило, используются именно сети, состоящие из последовательных слоев нейронов. Хотя любую сеть без обратных связей можно представить в виде последовательных слоев, именно наличие многих нейронов в каждом слое позволяет существенно ускорить вычисления используя матричные ускорители.
В немалой степени популярность персептронов обусловлена широким кругом доступных им задач. В общем виде они решают задачу
аппроксимации многомерных функций, т.е. построения многомерного отображения  обобщающего заданный
набор примеров
обобщающего заданный
набор примеров  .
.
В зависимости от типа выходных переменных (тип входных не имеет решающего значения), аппроксимация функций может принимать вид
- Классификации (дискретный набор выходных значений), или
- Регрессии (непрерывные выходные значения)
Многие практические задачи распознавания образов, фильтрации шумов, предсказания временных рядов и др. сводится к этим базовым прототипическим постановкам.
Причина популярности персептронов кроется в том, что для своего круга задач они являются во-первых универсальными, а во-вторых - эффективными с точки зрения вычислительной сложности устройствами. В этой лекции мы затронем оба аспекта.
Возможности многослойных персептронов
Изучение возможностей многослойных персептронов удобнее начать со свойств его основного компонента и одновременно простейшего персептрона - отдельного нейрона.
Нейрон - классификатор
Простейшим устройством распознавания образов, принадлежащим к рассматриваемому классу сетей, является одиночный нейрон, превращающий входной вектор признаков в скалярный ответ, зависящий от линейной комбинации входных переменных:

Здесь и далее мы предполагаем наличие у каждого нейрона дополнительного единичного входа с нулевым индексом, значение которого
постоянно: 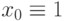 . Это позволит упростить выражения, трактуя все синаптические веса w j, включая порог w0, единым образом.
. Это позволит упростить выражения, трактуя все синаптические веса w j, включая порог w0, единым образом.
Скалярный выход нейрона можно использовать в качестве т.н. дискриминантной функции. Этим термином в теории распознавания образов
называют индикатор принадлежности входного вектора к одному из заданных классов. Так, если входные векторы могут принадлежать одному из
двух классов, нейрон способен различить тип входа, например, следующим образом:  если , входной вектор
принадлежит первому классу, в противном случае - второму.
если , входной вектор
принадлежит первому классу, в противном случае - второму.
Поскольку дискриминантная функция зависит лишь от линейной комбинации входов, нейрон является линейным дискриминатором. В
некоторых простейших ситуациях линейный дискриминатор - наилучший из возможных, а именно - в случае когда вероятности принадлежности
входных векторов к классу k задаются гауссовыми распределениями ![p_k(x) \infty exp[-(x-m_k)^T \sum^{-1}(x-m_k)]](/sites/default/files/tex_cache/04d5c21fe7d30baaa5c7f41512e74674.png) с
одинаковыми ковариационными матрицами
с
одинаковыми ковариационными матрицами  . В этом случае границы, разделяющие области, где вероятность одного класса
больше, чем вероятность остальных, состоят из гиперплоскостей
(см. рисунок 3.1 иллюстрирующий случай двух классов).
. В этом случае границы, разделяющие области, где вероятность одного класса
больше, чем вероятность остальных, состоят из гиперплоскостей
(см. рисунок 3.1 иллюстрирующий случай двух классов).

Рис. 3.1. Линейный дискриминатор дает точное решение в случае если вероятности принадлежности к различным классам - гауссовы, с одинаковым разбросом и разными центрами в пространстве параметров
В более общем случае поверхности раздела между классами можно описывать приближенно набором гиперплоскостей - но для этого уже потребуется несколько линейных дискриминаторов - нейронов.
Выбор функции активации
Монотонные функции активации  не влияют на классификацию. Но их значимость можно повысить, выбрав таким образом,
чтобы можно было трактовать выходы нейронов как вероятности принадлежности к соответствующему классу, что дает дополнительную
информацию при классификации. Так, можно показать, что в упомянутом выше случае гауссовых распределений вероятности, сигмоидная
функция активации нейрона
не влияют на классификацию. Но их значимость можно повысить, выбрав таким образом,
чтобы можно было трактовать выходы нейронов как вероятности принадлежности к соответствующему классу, что дает дополнительную
информацию при классификации. Так, можно показать, что в упомянутом выше случае гауссовых распределений вероятности, сигмоидная
функция активации нейрона 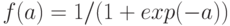 дает вероятность принадлежности к соответствующему классу.
дает вероятность принадлежности к соответствующему классу.
