Обучение с учителем: Распознавание образов

Градиентное обучение многослойных персептронов

Градиентное обучение

Наиболее общим способом оптимизации нейросети является итерационная (постепенная) процедура подбора весов, называемая обучением, в данном случае - обучением с учителем, поскольку опирается на обучающую выборку примеров 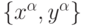, например - примеров правильной классификации.

Когда функционал ошибки задан, и задача сводится к его минимизации, можно предложить, например, следующую итерационную процедуру подбора весов: 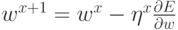или, что то же самое:

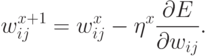
Здесь - темп обучения на шаге . Можно показать, что постепенно уменьшая темп обучения, например по закону 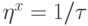, описанная выше процедура приводит к нахождению локального минимума ошибки.

Исторически наибольшую трудность на пути к эффективному правилу обучения многослойных персептронов вызвала процедура эффективного расчета градиента функции ошибки . Дело в том, что ошибка сети определяется по ее выходам, т.е. непосредственно связаная лишь с выходным слоем весов. Вопрос состоял в том, как определить ошибку для нейронов на скрытых слоях, чтобы найти производные по соответствующим весам. Нужна была процедура передачи ошибки с выходного слоя к предшествующим слоям сети, в направлении обратном обработке входной информации. Поэтому такой метод, когда он был найден, получил название метода обратного распространения ошибки.

Метод обратного распространения ошибки

Ключ к обучению многослойных персептронов оказался настолько простым и очевидным, что, как оказалось, неоднократно переоткрывался.

Между тем, в случае дифференцируемых функций активации рецепт нахождения производных по любому весу сети дается т.н. цепным правилом дифференцирования, известным любому первокурснику. Суть метода back-propagation - в эффективном воплощении этого правила.

Разберем этот ключевой для нейрокомпьютинга метод несколько подробнее. Обозначим входы n-го слоя нейронов . Нейроны этого слоя вычисляют соответствующие линейные комбинации:

и передают их на следующий слой, пропуская через нелинейную функцию активации (для простоты - одну и ту же, хотя это совсем необязательно): Для построения алгоритма обучения нам надо знать производную ошибки по каждому из весов сети: Таким образом, вклад в общую ошибку каждого веса вычисляется локально, простым умножением невязки нейрона на значение соответствующего входа. (Из-за этого, в случае когда веса изменяют по направлению скорейшего спуска 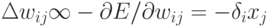, такое правило обучения называют дельта-правилом.)

Входы каждого слоя вычисляются последовательно от первого слоя к последнему во время прямого распространения сигнала:

, а невязки каждого слоя вычисляются во время обратного распространения ошибки от последнего слоя (где они определяются по выходам сети) к первому: Последняя формула получена применением цепного правила к производной и означает, что чем сильнее учитывается активация данного нейрона на следующем слое, тем больше его ответственность за общую ошибку.

Эффективность алгоритма back-propagation

Важность изложенного выше алгоритма back-propagation в том, что он дает чрезвычайно эффективный способ нахождения градиента функции ошибки . Если обозначить общее число весов в сети как W, то необходимое для вычисления градиента число операций растет пропорционально W, т.е. этот алгоритм имеет сложность O(W). Напротив, прямое вычисление градиента по формуле

потребовала бы W прямых прогонов через сеть, требующих O(W) операций каждый. Таким образом "наивный" алгоритм имеет сложность , что существенно хуже, чем у алгоритма back-propagation.