Нейронные сети и ...
Животные делятся на:
- принадлежащих Императору,
- набальзамированных,
- прирученных,
- сосунков,
- сирен,
- сказочных,
- отдельных собак,
- включенных в эту классификацию,
- бегающих, как сумасшедшие,
- бесчисленных,
- нарисованных тончайшей кистью из верблюжьей шерсти,
- прочих,
- разбивших цветочную вазу,
- издали напоминающих мух.
Нейрокомпьютинг имеет многочисленные точки соприкосновения с другими дисциплинами и их методами. В частности, теория нейронных сетей использует аппарат статистической механики и теории оптимизации. Области приложения нейрокомпьютинга подчас сильно пересекаются или почти совпадают со сферами применения математической статистики, теории нечетких множеств и экспертных систем. Связи и параллели нейрокомпьютинга чрезвычайно многообразны и свидетельствуют о его универсальности. В данной лекции, которую можно рассматривать как дополнительную, так как она требует несколько большей математической подготовки, мы поговорим только о наиболее важных из них.
Нейронные сети и статистика
Поскольку в настоящее время нейронные сети с успехом используются для анализа данных, уместно сопоставить их со старыми хорошо разработанными статистическими методами. В литературе по статистике иногда можно встретить утверждение, что наиболее часто применяемые нейросетевые подходы являются ни чем иным, как неэффективными регрессионными и дискриминантными моделями. Мы уже отмечали прежде, что многослойные нейронные сети действительно могут решать задачи типа регрессии и классификации. Однако, во-первых, обработка данных нейронными сетями носит значительно более многообразный характер - вспомним, например, активную классификацию сетями Хопфилда или карты признаков Кохонена, не имеющие статистических аналогов. Во-вторых, многие исследования, касающиеся применения нейросетей в финансах и бизнесе, выявили их преимущества перед ранее разработанными статистическими методами. Рассмотрим подробнее результаты сравнения методов нейросетей и математической статистики.
Являются ли нейронные сети языком описания?
Как уже отмечалось, некоторые статистики утверждают, что нейросетевые подходы к обработке данных являются просто заново переоткрытыми и переформулированными, но хорошо известными статистическими методами анализа. Иными словами, нейрокомпьютинг просто пользуется новым языком для описания старого знания. В качестве примера приведем цитату из Уоррена Сэрла:
Многие исследователи нейронных сетей являются инженерами, физиками, нейрофизиологами, психологами или специалистами по компьютерам, которые мало знают о статистике и нелинейной оптимизации. Исследователи нейронных сетей постоянно переоткрывают методы, которые известны в математической и статистической литературе десятилетиями и столетиями, но часто оказываются неспособными понять как работают эти методы
Подобная точка зрения, на первый взгляд, может показаться обоснованной. Формализм нейронных сетей действительно способен претендовать на роль универсального языка. Не случайно уже в пионерской работе МакКаллока и Питтса было показано, что нейросетевое описание эквивалентно описанию логики высказываний.
Я в действительности обнаружил, что с помощью техники, которую я разработал в работе1961 года (…), я мог бы легко ответить на все вопросы, которые мне задают специалисты по мозгу (...) или компьютерщики. Как физик, однако, я хорошо знал, что теория, которая объясняет все, на самом деле не объясняет ничего: в лучшем случае она является языком. Эдуардо Каянелло
Не удивительно поэтому, что статистики часто обнаруживают, что привычные им понятия имеют свои аналоги в теории нейронных сетей. Уоррен Сэрл составил небольшой словарик терминов, использующихся в этих двух областях.
| Нейронные сети | Статистические методы. |
|---|---|
| Признаки | переменные |
| входы | независимые переменные |
| выходы | предсказанные значения |
| целевые значения | зависимые переменные |
| ошибка | невязка |
| обучение, адаптация, самоорганизация | оценка |
| функция ошибки, функция Ляпунова | критерий оценки |
| обучающие образы (пары) | наблюдения |
| параметры сети: веса, пороги. | Оценочные параметры |
| нейроны высокого порядка | взаимодействия |
| функциональные связи | трансформации |
| обучение с учителем или гетероассоциация | регрессия и дискриминантный анализ |
| обучение без учителя или автоассоциация | сжатие данных |
| соревновательное обучение, адаптивная векторная квантизация | кластерный анализ |
| обобщение | интерполяция и экстраполяция |
В чем различие нейронных сетей и статистики?
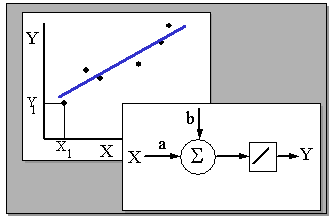
В чем же заключается сходство и различие языков нейрокомпьютинга и статистики в анализе данных. Рассмотрим простейший пример.
Предположим, что мы провели наблюдения и экспериментально измерили N пар точек, представляющих функциональную зависимость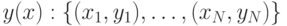 
.
Если попытаться провести через эти точки наилучшую прямую, что на языке статистики будет означать использование для описания
неизвестной зависимости линейной модели 
,
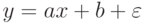(где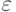 
обозначает шум при проведении наблюдения), то решение соответствующей проблемы линейной регрессии сведется к нахождению
оценочных значений параметров 
, 
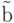минимизирующих сумму квадратичных невязок.
![\sum_{k=1}^N[y_k-(ax_k+b)]^2.](/sites/default/files/tex_cache/9107576f952d979e0183fdbe5a31c04a.png)
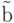Если параметры и найдены, то можно оценить значение y для любого значения x, то есть осуществить интерполяцию и экстраполяцию
данных.
Та же самая задача может быть решена с использованием однослойной сети с единственным входным и единственным линейным выходным нейроном. Вес связи a и порог b могут быть получены путем минимизации той же величины невязки (которая в данном случае будет называться среднеквадратичной ошибкой) в ходе обучения сети, например методом backpropagation. Свойство нейронной сети к обобщению будет при этом использоваться для предсказания выходной величины по значению входа.
При сравнении этих двух подходов сразу бросается в глаза то, что при описании своих методов статистика апеллирует к формулам и уравнениям, а нейрокомпьютинг к графическому описанию нейронных архитектур.
Еще одним существенным различием является то, что для методов статистики не имеет значения, каким образом будет минимизироваться невязка - в любом случае модель остается той же самой, в то время как для нейрокомпьютинга главную роль играет именно метод обучения. Иными словами, в отличие от нейросетевого подхода, оценка параметров модели для статистических методов не зависит от метода минимизации. В то же время статистики будут рассматривать изменения вида невязки, скажем на
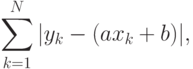
В отличие от нейросетевого подхода, в котором основное время забирает обучение сетей, при статистическом подходе это время тратится на тщательный анализ задачи. При этом опыт статистиков используется для выбора модели на основе анализа данных и информации, специфичной для данной области. Использование нейронных сетей - этих универсальных аппроксиматоров - обычно проводится без использования априорных знаний, хотя в ряде случаев оно весьма полезно. Например, для рассматриваемой линейной модели использование именно среднеквадратичной ошибки ведет к получению оптимальной оценки ее параметров, когда величина шума имеет нормальное распределение с одинаковой дисперсией для всех обучающих пар. В то же время если известно, что эти дисперсии различны, то использование взвешенной функции ошибки
![\sum_{k=1}^Nc_k[y_k-(ax_k+b)]^2](/sites/default/files/tex_cache/ef6e0da8e3ef15d8ba0d0d6049facb1f.png)
Помимо рассмотренной простейшей модели можно привести примеры других в некотором смысле эквивалентных моделей статистики и нейросетевых парадигм
| Нейронные сети | Статистические методы |
|---|---|
| Многослойный персептрон | Нелинейная (в т.ч. логистическая) регрессия, Дискриминантные модели |
| Автоассоциативный персептрон | Анализ главных компонент |
| Векторная квантизация | Кластеризация с k-средними |
| Сети нейронов высоких порядков | Полиномиальная регрессия |