|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Интегрирование логарифмических и экспоненциальных функций. Решение дифференциального уравнения Риша
Интегрирование логарифмических функций
Пусть  - независимая переменная над вычислимым
полем констант
- независимая переменная над вычислимым
полем констант  ,
,  - последовательность регулярных
мономов,
- последовательность регулярных
мономов, 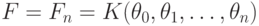 -
соответствующее поле элементарных функций,
-
соответствующее поле элементарных функций,  . Предположим, что
. Предположим, что 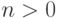 ,
,  - логарифм над
- логарифм над 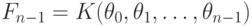 и что мы
умеем интегрировать функции из поля
и что мы
умеем интегрировать функции из поля 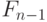 .
Опишем алгоритм, позволяющий найти неопределенный интеграл функции
.
Опишем алгоритм, позволяющий найти неопределенный интеграл функции  , если
он является элементарной функцией, или доказать, что в элементарных функциях
, если
он является элементарной функцией, или доказать, что в элементарных функциях  неинтегрируема.
неинтегрируема.
Пусть 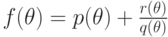 - разложение функции
- разложение функции  в сумму полинома
и правильной рациональной дроби (как рациональной функции от
в сумму полинома
и правильной рациональной дроби (как рациональной функции от  с коэффициентами
из поля
с коэффициентами
из поля 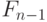 ). Прежде всего покажем, что можно отдельно
рассматривать задачу
для полиномиальной части
). Прежде всего покажем, что можно отдельно
рассматривать задачу
для полиномиальной части  и рациональной части
и рациональной части 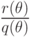 .
.
25.1. ЛЕММА (о разложении).
Элементарный интеграл функции 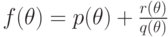 существует тогда и только тогда, когда существуют элементарные интегралы
функций
существует тогда и только тогда, когда существуют элементарные интегралы
функций  и
и ![\smash[t]{\frac {r(\theta )}{q(\theta
)}}](/sites/default/files/tex_cache/dc148847b61a52b6a85f636593b54327.png) .
.
ДОКАЗАТЕЛЬСТВО.
Согласно теореме Лиувилля, если элементарный интеграл
существует, то он имеет вид ![g=v_0+\smash[b]{\sum\limits_{i=1}^m}c_i\log
v_i](/sites/default/files/tex_cache/de9623df84ae4b7c5c97ee3b3b5f4e6e.png) , т. е.
функцию
, т. е.
функцию  можно представить в виде
можно представить в виде
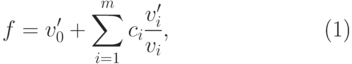 |
( 25.1) |
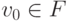 ,
,  - алгебраические над
- алгебраические над  константы,
константы, 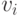
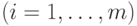 - элементы
из дифференциального поля, получающегося присоединением к
- элементы
из дифференциального поля, получающегося присоединением к 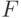 конечного числа
алгебраических над
конечного числа
алгебраических над  констант. Дифференцирование
констант. Дифференцирование 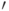 означает дифференцирование по
означает дифференцирование по  .
Рассматривая (25.1) как тождество в поле
.
Рассматривая (25.1) как тождество в поле 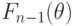 , мы без потери общности можем предполагать, что
, мы без потери общности можем предполагать, что 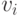
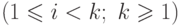 - нормированные (со старшим коэффициентом, равным 1) полиномы от
- нормированные (со старшим коэффициентом, равным 1) полиномы от  , а
, а 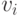 для
для 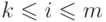 - элементы поля
- элементы поля 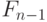 . Разложим
. Разложим 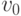 в сумму полинома
в сумму полинома 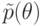 от
от  и правильной рациональной дроби
и правильной рациональной дроби  от
от  . Заметим, что
. Заметим, что 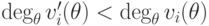 (используется то, что старший коэффициент равен 1 и
(используется то, что старший коэффициент равен 1 и 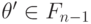 ).
Учитывая дифференциальное уравнение, которому удовлетворяет
).
Учитывая дифференциальное уравнение, которому удовлетворяет  , после дифференцирования
суммы
, после дифференцирования
суммы 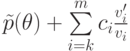 по
по  мы получаем полином от
мы получаем полином от  с коэффициентами в поле
с коэффициентами в поле 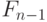 , а продифференцировав
по
, а продифференцировав
по  правильную рациональную функцию (от
правильную рациональную функцию (от  ),
снова получаем правильную
рациональную функцию. Лемма о разложении теперь следует из единственности
представления произвольной рациональной функции в виде суммы полинома и
правильной
рациональной функции.
),
снова получаем правильную
рациональную функцию. Лемма о разложении теперь следует из единственности
представления произвольной рациональной функции в виде суммы полинома и
правильной
рациональной функции.Интегрирование полиномиальной части
Сначала проинтегрируем полиномиальную часть  .
.
Пусть  ,
,  . Прежде всего покажем, что
. Прежде всего покажем, что 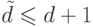 .
Для этого проверим, что при дифференцировании по
.
Для этого проверим, что при дифференцировании по  полинома от
полинома от  его степень
уменьшается не более, чем на 1. Учитывая, что
его степень
уменьшается не более, чем на 1. Учитывая, что  , видим, что степень полинома
, видим, что степень полинома  равна
равна  , если
, если  , т. е.
, т. е.  не является
константой.
Для того, чтобы степень полинома
не является
константой.
Для того, чтобы степень полинома  при дифференцировании по
при дифференцировании по  понизилась не менее, чем на два, требуется выполнение следующих условий:
понизилась не менее, чем на два, требуется выполнение следующих условий: 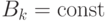 , т. е.
, т. е. 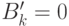 и
и 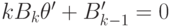 , т. е.
, т. е. 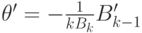 .
Интегрируя выписанное соотношение, получаем
.
Интегрируя выписанное соотношение, получаем  , где
, где  - константа интегрирования.
По предположению,
- константа интегрирования.
По предположению,  является регулярным мономом, т. е.
трансцендентен над полем
является регулярным мономом, т. е.
трансцендентен над полем 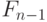 , которому принадлежит правая часть. Таким образом
полученное
противоречие показывает, что при дифференцировании по
, которому принадлежит правая часть. Таким образом
полученное
противоречие показывает, что при дифференцировании по  полинома
от
полинома
от  его степень понижается не более, чем на 1.
его степень понижается не более, чем на 1.
Интегрируем полиномиальную часть методом неопределенных коэффициентов.
Пусть 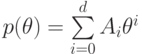 ,
, 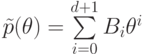 ,
, 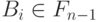 при
при  ,
, 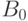 принадлежит некоторому элементарному расширению
поля
принадлежит некоторому элементарному расширению
поля 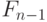 .
Как показано в предыдущем
абзаце, старший коэффициент
.
Как показано в предыдущем
абзаце, старший коэффициент 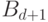 является константой, обозначим
ее
является константой, обозначим
ее 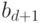 . Для нахождения остальных коэффициентов
. Для нахождения остальных коэффициентов 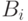 ,
,  ,
мы получаем, приравнивая коэффициенты при одинаковых степенях
,
мы получаем, приравнивая коэффициенты при одинаковых степенях  ,
систему дифференциальных уравнений
,
систему дифференциальных уравнений
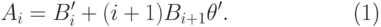 |
( 25.2) |
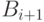 уже определен с точностью до
аддитивной
константы
уже определен с точностью до
аддитивной
константы 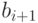 (в частности, можно считать, что
(в частности, можно считать, что 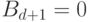 ).
Для определения константы
).
Для определения константы 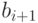 и элемента
и элемента 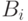 рассмотрим подробнее
уравнение (25.2).
Перепишем это уравнение в виде
рассмотрим подробнее
уравнение (25.2).
Перепишем это уравнение в виде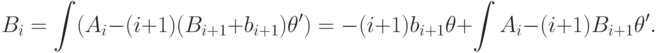
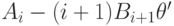 принадлежит полю
принадлежит полю 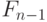 , и мы можем по предположению
индукции его проинтегрировать. Необходимым условием интегрируемости исходной
функции
в классе элементарных функций является то, что
, и мы можем по предположению
индукции его проинтегрировать. Необходимым условием интегрируемости исходной
функции
в классе элементарных функций является то, что  ,
где
,
где  - константа (алгебраическая над
- константа (алгебраическая над  ), а
), а 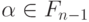 . Если же это условие выполнено, то мы
получаем значение
константы
. Если же это условие выполнено, то мы
получаем значение
константы 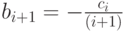 и значение коэффициента
и значение коэффициента 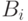 .
Интегрируя уравнение (25.2) при
.
Интегрируя уравнение (25.2) при 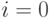 , т. е. вычисляя
, т. е. вычисляя 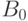 , нужно
отказаться от условия
, нужно
отказаться от условия  , достаточно, чтобы
существовал элементарный
интеграл
, достаточно, чтобы
существовал элементарный
интеграл 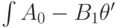 . Этот интеграл определяется с
точностью до аддитивной
константы, которая является константой интегрирования и не может быть
определена
при рассматриваемой постановке задачи.
. Этот интеграл определяется с
точностью до аддитивной
константы, которая является константой интегрирования и не может быть
определена
при рассматриваемой постановке задачи.