|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Лекция 10: Алгоритмы факторизации, основанные на выборе малого вектора в решетке
Теперь рассмотрим второй подход к решению задачи факторизации,
предложенный в
п. 16.1, а именно, выделяем
неприводимый в ![\mathbb Z [x]](/sites/default/files/tex_cache/ed6dece6199fb070fddfe66fd7b2327c.png) делитель многочлена
делитель многочлена  путем построения некоторой решетки и отысканием в ней "малого" вектора.
путем построения некоторой решетки и отысканием в ней "малого" вектора.
Общая схема факторизации
В самых общих чертах алгоритм выделения неприводимого множителя с использованием редуцированного базиса решетки имеет следующий вид:
А37. АЛГОРИТМ. (выделить-неприводимый-множитель
( 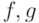 ))
))
![\begin{equation*}\\
\text{Дано:\quad$f(x) \in \mathbb Z [x]$, $\deg f(x) = m$}\\
\text{Надо:\quad \qquad $g(x) \in \mathbb Z [x]$, $g(x)$ неприводим в $\mathbb Z [x]$}\\
\text{Начало}\\
\text{выбрать полное нормированное поле $K$, содержащее $\mathbb Z $}\\
\text{ограничить степень неприводимого множителя, например,}\\
\text{\qquad $\deg g(x)\le n=m-1$}\\
\text{определить достаточную точность вычислений}\\
\text{найти с требуемой точностью неприводимый $h(x) \in
K[x]$, делящий $f(x)$}}\\
\text{найти с требуемой точностью неприводимый $h(x) \in K[x]$, делящий}\\
\text{\qquad $f(x)$}\\
\text{\qquad //В результате дальнейших вычислений будет найден}\\
\text{\qquad //неприводимый над $\mathbb Z $ многочлен, делящийся на $h(x)$.}\\
\text{сформировать решетку $L$, ввести на ней норму $\|\ \|$}\\
\text{\qquad //Искомый многочлен $g(x)$ должен принадлежать $L$}\\
\text{\qquad //и быть в ней вектором минимальной длины}\\
\text{оценить норму искомого $g(x)$,}\\
\text{\qquad //найти $B$ такое, что $\|g(x)\| < B$}\\
\text{если существует в $L$ вектор $v$, такой, что $\|v\| < B$ то}\\
\text{\qquad найти такой вектор $v$;}\\
\text{\qquad $g(x) := v$}\\
\text{иначе}\\
\text{\qquad $g(x) := f(x)$}\\
\text{конец если}\\
\text{Конец}
\end{equation*}](/sites/default/files/tex_cache/3cd47e14415414ed2b05caf4af41342a.png)
Некоторые дополнительные комментарии к сформулированному алгоритму.
Наиболее трудный этап в этом алгоритме заключается в нахождении
минимального
вектора решетки. Для решения этой задачи воспользуемся алгоритмом
построения
редуцированного базиса решетки. В общем случае этот алгоритм не позволяет
находить минимальный вектор в решетке, но находит вектор, длина которого
отличается от длины минимального не более, чем в 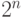 раз, где
раз, где  -
размерность решетки. Таким образом, на вводимую норму
-
размерность решетки. Таким образом, на вводимую норму  накладывается
более сильное условие:
накладывается
более сильное условие:  должна отличаться от нормы
любого взаимно
простого с
должна отличаться от нормы
любого взаимно
простого с 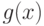 многочлена
многочлена ![w(x) \in \mathbb Z [x]](/sites/default/files/tex_cache/37a117631aae13c6ff5b2f624c044044.png) не
менее, чем в
не
менее, чем в 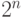 раз.
Константа
раз.
Константа  должна быть выбрана таким образом, чтобы выполнялись
неравенства
должна быть выбрана таким образом, чтобы выполнялись
неравенства 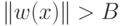 и
и 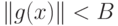 и алгоритм
построения редуцированного базиса
решетки давал положительный ответ на вопрос о существовании вектора, длина
которого меньше
и алгоритм
построения редуцированного базиса
решетки давал положительный ответ на вопрос о существовании вектора, длина
которого меньше  , в том и только в том случае, когда
, в том и только в том случае, когда 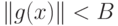 . Искомая
норма
. Искомая
норма 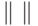 зависит от неприводимого над
зависит от неприводимого над ![K[x]](/sites/default/files/tex_cache/a77a9131b3530308247cff0e3c92321a.png) многочлена
многочлена 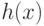 , при этом
нужно помнить, что многочлен
, при этом
нужно помнить, что многочлен 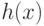 мы вычисляем с некоторой
точностью (не
абсолютной), эта точность должна быть достаточно хорошей для того, чтобы
сформулированные выше условия на
мы вычисляем с некоторой
точностью (не
абсолютной), эта точность должна быть достаточно хорошей для того, чтобы
сформулированные выше условия на 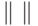 остались
справедливыми.
остались
справедливыми.
Нахождение с требуемой точностью неприводимого множителя ![h(x) \in
K[x]](/sites/default/files/tex_cache/c3a100292f8f1516a689d5d1008c0fe3.png) можно
разделить на два этапа: нахождение нулевого приближения и уточнение
множителя.
можно
разделить на два этапа: нахождение нулевого приближения и уточнение
множителя.
Перепишем алгоритм A37 с учетом сделанных замечаний.
АЛГОРИТМ выделить-неприводимый-множитель
(многочлены 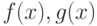 )
)
![\begin{equation*}\\
\text{Дано:\quad $f(x) \in \mathbb Z [x], \deg f(x) = m$}\\
\text{Надо:\quad \qquad $g(x) \in \mathbb Z [x], g(x)$ неприводим в $\mathbb Z [x]$}\\
\text{Начало}\\
\text{выбрать полное нормированное поле $K$, содержащее $\mathbb Z $}\\
\text{ограничить сверху степень неприводимого множителя}\\
\text{\qquad натуральным числом $n$, например, $n:=m-1$}\\
\text{определить достаточную точность вычислений}\\
\text{найти нулевое приближение неприводимого $h(x) \in K[x]$}\\
\text{цикл пока не достигнута требуемая точность}\\
\text{\qquad уточнить $h(x) \in K[x]$}\\
\text{конец цикла}\\
\text{сформировать решетку $L$, ввести на ней норму $\|\ \|$}\\
\text{оценить норму искомого $g(x)$: $\|g(x)\| < B$}\\
\text{редуцировать базис решетки $L$}\\
\text{если $L$.базис[0] $< B$ то}\\
\text{\qquad $g(x) := L$.базис[0]}\\
\text{конец если}\\
\text{Конец}
\end{equation*}](/sites/default/files/tex_cache/77e7decc4188851370d951f15ad87dac.png)
Рассмотрим основные особенности алгоритма факторизации при
использовании
архимедовой и  - адической метрики на поле
- адической метрики на поле  .
В первом случае в качестве
поля
.
В первом случае в качестве
поля  выберем поле комплексных чисел
выберем поле комплексных чисел 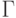 , во втором
- поле
, во втором
- поле  - адических
чисел
- адических
чисел 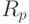 .
.
