|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Алгоритмы вычисления размерностных многочленов
В предыдущем параграфе (см.12.7) мы отмечали, что
размерностный многочлен любого множества  равен
размерностному
многочлену, ассоциированному с множеством всех минимальных элементов множества
равен
размерностному
многочлену, ассоциированному с множеством всех минимальных элементов множества  . Значит, достаточно уметь вычислять размерностные многочлены
только
для конечных множеств
. Значит, достаточно уметь вычислять размерностные многочлены
только
для конечных множеств 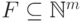 (более того, можно
предполагать, что
элементы множества
(более того, можно
предполагать, что
элементы множества  попарно несравнимы относительно порядка
произведения).
попарно несравнимы относительно порядка
произведения).
Пусть  обозначает
обозначает  -матрицу над
-матрицу над 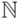 , т. е. матрицу с
, т. е. матрицу с  строками и
строками и  столбцами, элементы которой -
неотрицательные целые числа. Рассматривая строки матрицы
столбцами, элементы которой -
неотрицательные целые числа. Рассматривая строки матрицы 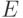 как
элементы множества
как
элементы множества  и обозначая
и обозначая  -ю строку
-ю строку  через
через 
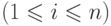 , мы получим подмножество
, мы получим подмножество  ,
ассоциированное с
,
ассоциированное с 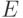 . Напомним, что размерностный многочлен
. Напомним, что размерностный многочлен  -матрицы
-матрицы 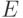 в точности совпадает с
размерностным многочленом множества
в точности совпадает с
размерностным многочленом множества 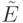 и называется многочленом Гильберта матрицы
и называется многочленом Гильберта матрицы 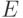 .
.
Пусть  - размерностный многочлен
- размерностный многочлен  -матрицы
-матрицы 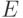 над
над 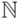 .
По определению
.
По определению  для всех достаточно
больших
для всех достаточно
больших  , где
, где 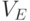 обозначает множество всех элементов
из
обозначает множество всех элементов
из 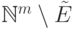 ,
которые не превосходят ни одного элемента из
,
которые не превосходят ни одного элемента из 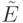 относительно порядка произведения,
так что
относительно порядка произведения,
так что 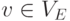 если и только если неравенство
если и только если неравенство  не выполняется ни для одного
не выполняется ни для одного 
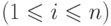 .
.
Как было отмечено, для того, чтобы уметь вычислять размерностный многочлен
любого
подмножества в  , достаточно уметь вычислять его для
любой
, достаточно уметь вычислять его для
любой  -матрицы
-матрицы 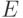 над
над 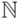 .
Один из методов вычисления основан на формуле (12,4).
.
Один из методов вычисления основан на формуле (12,4).
Пусть  обозначает
обозначает  -матрицу над
-матрицу над 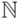 .
Воспользуемся следующими обозначениями, введенными в параграфе 12:
.
Воспользуемся следующими обозначениями, введенными в параграфе 12:

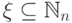 и
и 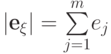 .
По предложению 12.9 (см. 12.4) мы можем записать
.
По предложению 12.9 (см. 12.4) мы можем записать
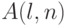
 обозначает множество всех
обозначает множество всех 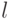 -элементных подмножеств
множества
-элементных подмножеств
множества  .
.Пользуясь выписанной формулой, можно
предложить следующий алгоритм вычисления
размерностного многочлена  , ассоциированного с
, ассоциированного с  -матрицей
-матрицей 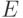 .
.

Легко видеть, что асимптотическая сложность алгоритма A9
имеет порядок  , где
, где  - число
строк матрицы
- число
строк матрицы 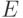 (по теореме 12.8 мы
можем считать, что строки попарно несравнимы относительно порядка произведения
на
(по теореме 12.8 мы
можем считать, что строки попарно несравнимы относительно порядка произведения
на  ).
).
Мора и Меллер модифицировали алгоритм вычисления многочлена
Гильберта
[
27
]
. Их алгоритм
основан на следующих соображениях. Легко видеть, что в формуле (12.5)
может выполняться равенство  для двух различных подмножеств
для двух различных подмножеств  и
и  множества
множества  , таких, что
, таких, что  и
и  являются четным и нечетным числами соответственно
(мы пользуемся обозначениями предложения 12.9). Тогда соответствующие
слагаемые в формуле (12.5) сократятся. Более того, можно сгруппировать
все слагаемые,
соответствующие одному и тому же элементу
являются четным и нечетным числами соответственно
(мы пользуемся обозначениями предложения 12.9). Тогда соответствующие
слагаемые в формуле (12.5) сократятся. Более того, можно сгруппировать
все слагаемые,
соответствующие одному и тому же элементу  .
.
Пусть  - множество всех элементов
- множество всех элементов 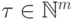 , которые равны, по крайней мере, одному из элементов
, которые равны, по крайней мере, одному из элементов 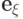 , где
, где 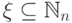 .
Тогда из формулы (12.4) следует, что
.
Тогда из формулы (12.4) следует, что
 |
( 13.1) |
 обозначает сумму всех координат вектора
обозначает сумму всех координат вектора  , и
, и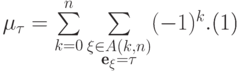 |
( 13.2) |
Очевидно, если матрица 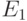 получена присоединением строки
получена присоединением строки 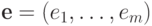 к матрице
к матрице 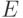 ,
,  и
и  - множество коэффициентов (13.2) в соотношении
(13.1) для многочлена
- множество коэффициентов (13.2) в соотношении
(13.1) для многочлена 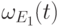 , так что
, так что

 , то
, то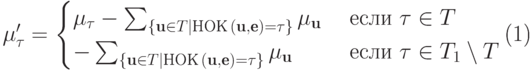 |
( 13.3) |
Таким образом, вычисление многочлена  , т. е.
вычисление коэффициентов
, т. е.
вычисление коэффициентов  , в (13.1) может быть основано на
формуле (13.3),
если мы начнем с пустой матрицы (число строк которой равно нулю и многочлен
Гильберта которой равен
, в (13.1) может быть основано на
формуле (13.3),
если мы начнем с пустой матрицы (число строк которой равно нулю и многочлен
Гильберта которой равен  ) и последовательно будем присоединять строки матрицы
) и последовательно будем присоединять строки матрицы 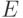 , вычисляя множество
, вычисляя множество  и коэффициенты
и коэффициенты 
 на каждом шаге
(см. алгоритм A10 ).
на каждом шаге
(см. алгоритм A10 ).
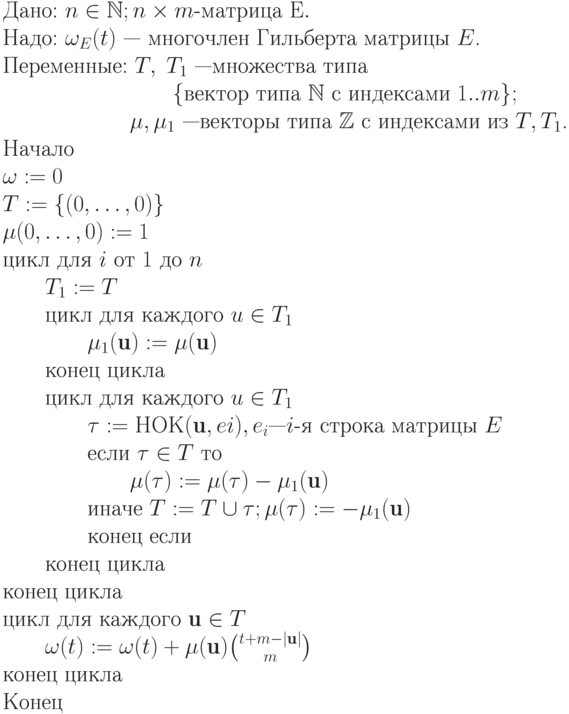
Поскольку на  -м шаге
-м шаге 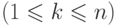 алгоритма
каждый элемент
алгоритма
каждый элемент  является наименьшим общим кратным некоторого подмножества
множества
является наименьшим общим кратным некоторого подмножества
множества 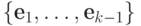 (т. е.
(т. е. 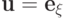 для некоторого
для некоторого 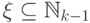 ), существует не более
), существует не более  различных
возможностей для
выбора каждой координаты вектора
различных
возможностей для
выбора каждой координаты вектора 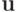 , следовательно, на
, следовательно, на  -м шаге
-м шаге 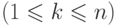 множество
множество 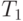 содержит не более
содержит не более 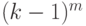 элементов. Вычисление
всех элементов
элементов. Вычисление
всех элементов  требует не более
требует не более  сравнений, и можно предполагать
(используя достаточно эффективный метод сортировки), что число проверок на
принадлежность
сравнений, и можно предполагать
(используя достаточно эффективный метод сортировки), что число проверок на
принадлежность  не превосходит
не превосходит  для всех
достаточно больших
для всех
достаточно больших  . Таким образом, асимптотическая
сложность (по
. Таким образом, асимптотическая
сложность (по  ) алгоритма A10 не превосходит
) алгоритма A10 не превосходит ![m\sum\limits_{k=2}^n\left[(k-1)^m+k^m\log k\right]](/sites/default/files/tex_cache/0c11e2af26a27eb27cac9134b6172047.png) . Поскольку
. Поскольку ![m
\sum\limits_{k=2}^n\left[ (k - 1)^m+ k^m\log k\right] < 2m
\sum\limits_{k=2}^n k^m \log k](/sites/default/files/tex_cache/dfd3ab5c4df39da78da96568132e9189.png) , асимптотическая сложность имеет порядок
, асимптотическая сложность имеет порядок  .
.
Следующие алгоритмы вычисления размерностного многочлена произвольной  -матрицы
-матрицы 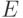 сводят эту задачу к
аналогичной задаче для матрицы
с числом строк меньшим, чем в
сводят эту задачу к
аналогичной задаче для матрицы
с числом строк меньшим, чем в 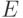 . По одному из этих алгоритмов
(см. ниже алгоритм A11 ) можно
вычислить коэффициенты
. По одному из этих алгоритмов
(см. ниже алгоритм A11 ) можно
вычислить коэффициенты  в (13.1) размерностного многочлена
в (13.1) размерностного многочлена  , что дает выражение для размерностного многочлена.
Для обоснования этого алгоритма нам нужны некоторые свойства коэффициентов
, что дает выражение для размерностного многочлена.
Для обоснования этого алгоритма нам нужны некоторые свойства коэффициентов  , которые сформулированы ниже в леммах
13.1-13.5, 13.7 и 13,9. Последняя из этих лемм
устанавливает соотношения, на которых основан алгоритм вычисления
, которые сформулированы ниже в леммах
13.1-13.5, 13.7 и 13,9. Последняя из этих лемм
устанавливает соотношения, на которых основан алгоритм вычисления  .
.
Чтобы подчеркнуть зависимость коэффициентов  от
матрицы
от
матрицы 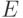 , будем обозначать
эти коэффициенты
, будем обозначать
эти коэффициенты 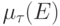 и продолжим это обозначение на
случай произвольного
вектора
и продолжим это обозначение на
случай произвольного
вектора  , полагая
, полагая

 - множество всех элементов
- множество всех элементов 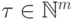 , таких, что
каждый
, таких, что
каждый  равен либо
равен либо  , либо наименьшему
общему кратному некоторых строк
матрицы
, либо наименьшему
общему кратному некоторых строк
матрицы 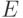 ; элементы множества
; элементы множества  будем называть допустимыми элементами или допустимыми векторами
матрицы
будем называть допустимыми элементами или допустимыми векторами
матрицы 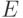 .)
.)
 .
.