|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Алгоритмы Кронекера. Разложение на множители, свободные от квадратов. Факторизация
Алгоритмы Кронекера
Алгоритм Кронекера находит для данного многочлена ![f(x)\in\mathbb Z[x]](/sites/default/files/tex_cache/7e183a630f334a98d75b9005df56b234.png) многочлен
многочлен ![f_1(x)\in \mathbb Z[x]](/sites/default/files/tex_cache/3c1774b8c2d8137b39aa6991d1e33388.png) ,
такой, что
,
такой, что 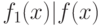 , или доказывает, что такого многочлена нет. Алгоритм
Кронекера
основан на следующих соображениях:
, или доказывает, что такого многочлена нет. Алгоритм
Кронекера
основан на следующих соображениях:
- если степень многочлена
 равна
равна  , то степень хотя бы одного множителя
, то степень хотя бы одного множителя  многочлена
многочлена  не превосходит
не превосходит ![[n/2]](/sites/default/files/tex_cache/1df61e7f2446684a7a300e9420d62011.png) ;
; - значения как
 , так и
, так и  в целых точках —
целые числа, причем
в целых точках —
целые числа, причем 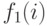 делит
делит 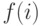 для любого
целого
для любого
целого  ;
; - при фиксированном
 , если
, если  , то
, то 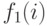 может принимать только конечное множество значений,
состоящее из
делителей числа
может принимать только конечное множество значений,
состоящее из
делителей числа 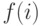 ;
; - коэффициенты многочлена
 однозначно восстанавливаются по
его значениям в
однозначно восстанавливаются по
его значениям в ![[n/2]+1](/sites/default/files/tex_cache/c26d006f41ade7a427442be68bee0854.png) точке.
точке.
Таким образом, для  получается конечное число возможностей;
непосредственным
делением проверяем, получили ли делитель многочлена
получается конечное число возможностей;
непосредственным
делением проверяем, получили ли делитель многочлена  .
.
Перепишем алгоритм Кронекера в соответствии со сделанными выше замечаниями.
![\begin{equation}\\
\text{Дано:\quad $f\in\mathbb Z[x]$;} \\
\text{Надо: \qquad $g\in\mathbb Z[x]$;} \\
\text{\qquad успех $\in\EuScript L$ \quad // "да" , если множитель найден.}\\
\text{Обозначения:} \\
\text{\qquad $n == f$.степень} \\
\text{\qquad $m == g$.степень} \\
\text{\qquad $f(i)$,\quad $i\in \mathbb Z == $значение многочлена
$f$ в точке $i$.}\\
\text{Переменные:} \\
\text{\qquad $M$ - множество элементов типа целое }\\
\text{\qquad $U$ - множество 'динамических' векторов
элементов типа $\mathbb Z$}\\
\text{Начало}\\
\text{успех $:=$ "нет"}\\
\text{цикл для $i$ от $0$ до $[n/2]$ пока не успех} \\
\text{\qquad // проверка, что среди целых чисел от $0$ до
$[\frac n2]$ нет корней $f(x)$}\\
\text{\qquad если $f(i)=0$, то}\\
\text{\qquad \qquad успех $:=$ "да"} \\
\text{\qquad \qquad $g :=x-i$}\\
\text{\qquad \qquad $m :=1$}\\
\text{\qquad конец если}\\
\text{конец цикла}\\
\text{если не успех, то} \\
\text{\qquad $U :=$ множество делителей числа $f(0)$}\\
\text{\qquad цикл для $i$ от $1$ до
$[n/2]$ пока не успех } \\
\text{\qquad \qquad \qquad // поиск множителя степени $i$}\\
\text{\qquad \qquad $M := $ множество делителей числа $ f(i)$}\\
\text{\qquad \qquad $U := U\times M$\qquad // прямое произведение}\\
\text{\qquad \qquad цикл для каждого
$u$ из $U$ пока не успех}\\
\text{\qquad \qquad \qquad построить многочлен $g$ степени $i$, такой, что}\\
\text{\qquad \qquad \qquad $g(j) = u(j)$ для $j=0..i$}\\
\text{\qquad \qquad \qquad если $f$ делится на
$g$, то}\\
\text{\qquad \qquad \qquad \qquad успех $ := $ "да" } \\
\text{\qquad \qquad \qquad \qquad $m := i$}\\
\text{\qquad \qquad \qquad конец если}\\
\text{\qquad \qquad конец цикла}\\
\text{\qquad конец цикла}\\
\text{конец если}\\
\text{Конец}
\end{equation}](/sites/default/files/tex_cache/8c8b9483c933fba3c2e9cedd68953009.png)
14.1. ЗАМЕЧАНИЕ.
Достаточно научиться разлагать на множители многочлены со старшим
коэффициентом, равным 1. Действительно, если старший
коэффициент равен  , то домножив на
, то домножив на 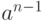 и
сделав замену
и
сделав замену  , сводим задачу к этому случаю.
После ее решения остается сделать обратную замену и сократить на общий
множитель
, сводим задачу к этому случаю.
После ее решения остается сделать обратную замену и сократить на общий
множитель 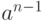 . Однако
этот метод обычно оказывается неэффективным: из-за увеличения коэффициентов
ухудшаются различные оценки и скорость работы алгоритмов. Поэтому
в большинстве работающих алгоритмов таких преобразований не производится.
. Однако
этот метод обычно оказывается неэффективным: из-за увеличения коэффициентов
ухудшаются различные оценки и скорость работы алгоритмов. Поэтому
в большинстве работающих алгоритмов таких преобразований не производится.
Другое решение задачи факторизации "за конечное число шагов" следует из
того, что коэффициенты делителя - целые числа
и их абсолютная
величина ограничена сверху некоторой функцией от
коэффициентов многочлена  . В
"Алгоритмы Кронекера. Разложение на множители, свободные от квадратов. Факторизация"
мы нашли некоторые оценки для этих коэффициентов.
Они еще понадобятся нам в дальнейшем.
. В
"Алгоритмы Кронекера. Разложение на множители, свободные от квадратов. Факторизация"
мы нашли некоторые оценки для этих коэффициентов.
Они еще понадобятся нам в дальнейшем.
Задача разложения на неприводимые множители
"за конечное число шагов" многочленов от нескольких переменных с
"классической" точки зрения
решена также примерно сто лет назад. Соответствующий алгоритм также носит
имя Кронекера и
для некоторых областей коэффициентов (например,
для поля комплексных чисел 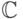 ) остается единственным известным
алгоритмом решения этой задачи. Для многочленов с
коэффициентами из кольца
целых чисел, или из кольца алгебраических чисел,
или из конечного поля и некоторых других получены в последнее время новые,
более быстрые алгоритмы. Общая схема этих
алгоритмов достаточно
близка к соответствующим алгоритмам факторизации
одномерных многочленов, хотя некоторые отличия
весьма существенны. Изложение современных алгоритмов факторизации многомерных
многочленов не
входит в число вопросов, освещаемых в данном пособии. Читателю,
интересующемуся этой задачей,
следует обратиться к специальной литературе.
) остается единственным известным
алгоритмом решения этой задачи. Для многочленов с
коэффициентами из кольца
целых чисел, или из кольца алгебраических чисел,
или из конечного поля и некоторых других получены в последнее время новые,
более быстрые алгоритмы. Общая схема этих
алгоритмов достаточно
близка к соответствующим алгоритмам факторизации
одномерных многочленов, хотя некоторые отличия
весьма существенны. Изложение современных алгоритмов факторизации многомерных
многочленов не
входит в число вопросов, освещаемых в данном пособии. Читателю,
интересующемуся этой задачей,
следует обратиться к специальной литературе.
Ниже излагаем многомерный алгоритм Кронекера для задачи, поставленной следующим образом.
Пусть 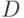 - область целостности с однозначным разложением
на множители,
- область целостности с однозначным разложением
на множители, ![f(x_1,\dots,x_n)\in D[x_1,\dots, x_n]](/sites/default/files/tex_cache/94ed491c32252f4d1d38ac4b8e3fb193.png) .
Требуется разложить
.
Требуется разложить  на неприводимые множители.
на неприводимые множители.
Многомерный алгоритм Кронекера
А17. АЛГОРИТМ (Кронекера_многомерный).
![\begin{equation}\\
\text{\textbf{Дано:}\quad $f\in\mathbb Z[x_1,\dots,x_n]$} \\
\text{\textbf{Надо:} \qquad $G$ - разложение} \\
\text{\textbf{Переменные:}} \\
\text{\qquad многочлен $\bar f\in\mathbb Z[y]$,} \\
\text{\qquad разложение $\bar G$ многочлена $\bar f$ }\\
\text{\qquad множество $M$ элементов типа $\mathbb Z$}\\
\textbf{Идея реализации }
\text{\qquad Редуцировать задачу к одномерному случаю, }\\
\text{\qquad путем введения новой неизвестной и заменой всех}\\
\text{\qquad переменных достаточно высокими степенями этой}\\
\text{\qquad неизвестной. Факторизовать получившийся многочлен. }\\
\text{\qquad Выполнить обратную подстановку, пробным делением}\\
\text{\qquad убедиться, получено ли желаемое разложение.}\\
\textbf{Начало} \\
\text{выбрать целое $d$ большее, чем степени отдельных переменных в $f$}\\
\text{заменить все переменные степенями новой неизвестной $y$:}\\
\text{$\bar f(y) := S_d(f) = f (y, y^d,\dots, y^{d^{n-1}})$}.\\
\text{разложить $\bar f(y)$ на неприводимые множители, т. е. }\\
\text{$ \bar f(y) = \bar g_1 (y)\dots\bar g_s(y),\qquad g_i(y)\in\mathbb Z[y],\quad 1\le
i\le s.$}\\
\text{$G. число_множителей := 1$}\\
\text{$m := 1$}\\
\text{$M := \{1,\dots, s\}$}\\
\text{\textbf{цикл пока} $m\le [s/2]$}\\
\text{\qquad \textbf{цикл для каждого }подмножества $\{i_1,\dots,i_m\}\subset M$ \textbf{пока} $ m\le [\frac s2]$}\\
\text{\qquad \qquad $g_{i_1,\dots,i_m}(x_1,\dots,x_n) :=S_d^{-1}\left(\bar g_{i_1}(y)\bar
g_{i_2}(y)\dots\bar g_{i_m}(y)\right)$ }\\
\text{\qquad \qquad \textbf{если} $f$ делится на $g$ \textbf{то} }\\
\text{\qquad \qquad \qquad $G.$ множитель $[G.$ число\_множителей ] $:= g$}\\
\text{\qquad \qquad \qquad $G$. число\_множителей} $:=G$. число\_множителей $+1$}\\
\text{\qquad \qquad \qquad $f := f/g$}\\
\text{\qquad \qquad \qquad $s := s - m$}\\
\text{\qquad \qquad \qquad $M$. удалить $\{i_1, i_2,\dots, i_m\}$}\\
\text{\qquad \qquad \textbf{конец если}}\\
\text{\qquad \textbf{конец цикла}}\\
\text{\qquad $m := m + 1$}\\
\text{\textbf{конец цикла}}\\
$G$. множитель $[G$. число\_множителей $] := f$\\
\text{\textbf{Конец}}
\end{equation}](/sites/default/files/tex_cache/c5438e536f574558eaf33c5c1af19394.png)
В этом алгоритме обратное преобразование 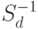 определяется
на одночленах по формуле
определяется
на одночленах по формуле

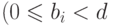 для
для 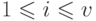 ,
,  , далее
, далее 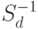 распространяется по линейности.
распространяется по линейности.