|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Лекция 10: Алгоритмы факторизации, основанные на выборе малого вектора в решетке
Архимедова метрика
При использовании архимедовой метрики на поле рациональных чисел  в
качестве полного нормированного расширения поля
в
качестве полного нормированного расширения поля  возьмем поле
комплексных
чисел
возьмем поле
комплексных
чисел  . В комплексном случае неприводимый многочлен
. В комплексном случае неприводимый многочлен ![h(x)
\in K[x]](/sites/default/files/tex_cache/af1f00f5736efd7e654e0fb03bdb6b41.png) является
линейным, мы можем считать его нормированным, т.е.
является
линейным, мы можем считать его нормированным, т.е.  для
некоторого
для
некоторого 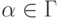 . Вычисление
. Вычисление  сводится к нахождению
комплексного корня многочлена
сводится к нахождению
комплексного корня многочлена  , что можно сделать с
произвольной наперед
заданной точностью. Решетка
, что можно сделать с
произвольной наперед
заданной точностью. Решетка  совпадает в этом случае с
совпадает в этом случае с 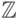 -модулем всех
многочленов с целыми коэффициентами степени
-модулем всех
многочленов с целыми коэффициентами степени  . Норму
многочлена
. Норму
многочлена  определим следующим образом:
определим следующим образом:  ,
где
,
где  - норма комплексного числа,
- норма комплексного числа,  - обычная евклидова норма на
пространстве многочленов, а
- обычная евклидова норма на
пространстве многочленов, а 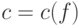 - некоторая
константа, зависящая от
исходного многочлена
- некоторая
константа, зависящая от
исходного многочлена  . При вычислениях на ЭВМ
. При вычислениях на ЭВМ  задается в виде
задается в виде 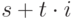 , где
, где  и
и  -
рациональные числа. Пусть
-
рациональные числа. Пусть  - точность
вычисления
- точность
вычисления  , т.е.
, т.е.  . Введенная выше
норма будет зависеть от точности, с которой вычислено значение корня
. Введенная выше
норма будет зависеть от точности, с которой вычислено значение корня  .
Таким образом, для обоснования алгоритма достаточно показать, что для
произвольно заданного многочлена
.
Таким образом, для обоснования алгоритма достаточно показать, что для
произвольно заданного многочлена ![f(x) \in \mathbb Z [x]](/sites/default/files/tex_cache/0b130046c7d3c4b117346f1302e7591b.png) можно явно
вычислить
положительные числа
можно явно
вычислить
положительные числа  ,
,  и
и  , такие,
что норма
, такие,
что норма  , которая определена
значением корня
, которая определена
значением корня  многочлена
многочлена  , вычисленного с
точностью
, вычисленного с
точностью 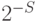 , и
константой
, и
константой  , удовлетворяет условиям:
, удовлетворяет условиям:
 |
( 21.1) |
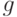 - минимальный многочлен для
- минимальный многочлен для  над
над 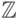 ,
,  - ранг решетки
- ранг решетки  ,
, |
( 21.2) |
![p \in \mathbb Z [x]](/sites/default/files/tex_cache/bb9dfd7969e272a2636f1bf9543d9a82.png) , не делящегося на
, не делящегося на 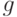 .
.После этого задача сводится к построению редуцированного базиса решетки.
Цель
данного раздела - показать, что числа  ,
,  и
и  можно выбрать следующим
образом:
можно выбрать следующим
образом:
 |
( 21.3) |
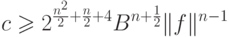 |
( 21.4) |
 |
( 21.5) |
 ,
,  ,
,  . Отметим, что для использования
приведенных выше формул нам удобно поменять местами некоторые команды
алгоритма.
. Отметим, что для использования
приведенных выше формул нам удобно поменять местами некоторые команды
алгоритма.А38. АЛГОРИТМ (выделить-неприводимый-множитель).
![\begin{equation*}\\
\text{Дано:\qquad $f(x) \in \mathbb Z [x], \deg f(x) = m$}\\
\text{Надо:\quad\qquad $g(x) \in \mathbb Z [x],g(x)$ неприводим в $\mathbb Z [x]$}\\
\text{Переменные:\quad решетка $L$} \\
\text{\qquad $S\in\mathbb Z $, $B,c\in\mathbb R $}\\
\text{Начало}\\
\text{$L$.ранг $:= m$}\\
\text{$n:=m-1$}\\
\text{$B:= \binom {2n}n \|f\|^2 + 1 ;$}\\
\text{$\displaystyle c := 2^{\frac{n^2}2 + \frac n2 + 4} B^{n+1/2}
\|f\|^{n-1}$}\\
\text{$S:=[\log_2 (c\cdot 4n \|f\|(2 + \|f\|)^{n-1})] + 1.$}\\
\text{найти комплексный корень $(f(x),\alpha,2^{-S})$}\\
\text{цикл для $i$ от $0$ до $n$ }\\
\text{\qquad $L$.базис$[i] := x^i$}\\
\text{конец цикла}\\
\text{редуцировать базис $(L)$}\\
\text{если $||L$.базис$[0]|| < B$ то}\\
\text{\qquad $g(x) := L$.базис$[0]$}\\
\text{иначе}\\
\text{\qquad $g(x) := f(x)$}\\
\text{конец если}\\
\text{Конец}
\end{equation*}](/sites/default/files/tex_cache/f501ca232816dd853b979a621d2dd1e8.png)
В получившейся версии алгоритма осталось детализировать два предписания:
- найти комплексный корень
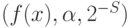 ;
; - редуцировать базис
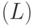 .
.
Нахождение комплексных корней многочлена представляет собой одну из классических задач вычислительной математики, мы не останавливаемся на ней. Алгоритм редуцирования базиса решетки изложен в параграфе 20.
Обоснование выбора значений B, c, S.
Пусть ![f \in \mathbb Z [x]](/sites/default/files/tex_cache/0e4e44cdf75db9681d6748087fc86f71.png) - примитивный многочлен степени
- примитивный многочлен степени  и
и  -
корень многочлена
-
корень многочлена  . Предположим, что
. Предположим, что ![h \in \mathbb Z [x]](/sites/default/files/tex_cache/8c1a5cc476baa0dc680962fed98f8589.png) - минимальный многочлен
для
- минимальный многочлен
для  . Очевидно, что
. Очевидно, что  - неприводимый
множитель многочлена
- неприводимый
множитель многочлена  . Цель
этого параграфа состоит в том, чтобы показать, как вычисление
. Цель
этого параграфа состоит в том, чтобы показать, как вычисление  с
достаточной точностью дает нам возможность определить
многочлен
с
достаточной точностью дает нам возможность определить
многочлен  .
.
В данном параграфе символ  используется для
обозначения степени
многочлена (
используется для
обозначения степени
многочлена (  ,
,  и
т.д.).
и
т.д.).
21.1. ПРЕДЛОЖЕНИЕ. Пусть  ,
, 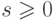 и предположим, что
и предположим, что  удовлетворяет
неравенству
удовлетворяет
неравенству
 |
( 21.6) |
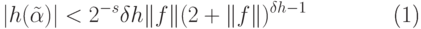 |
( 21.7) |
ДОКАЗАТЕЛЬСТВО.
Для доказательства этого предложения нам потребуются оценки  (так как
(так как  - корень многочлена
- корень многочлена  ) и
оценки коэффициентов многочлена
) и
оценки коэффициентов многочлена
 |
( 21.8) |
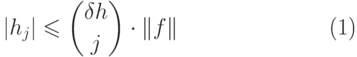
Собственно доказательство проводится путем разложения  в
ряд Тейлора в
окрестности точки
в
ряд Тейлора в
окрестности точки  и несложных вычислений с использованием
приведенных
оценок.
и несложных вычислений с использованием
приведенных
оценок.
Следующий этап вычислений заключается в приближении с точностью  значений
значений  рациональными числами с не слишком
большими знаменателями (чтобы не проводить
вычислений со слишком большими знаменателями). После этого, выбрав произвольным
образом рациональное число
рациональными числами с не слишком
большими знаменателями (чтобы не проводить
вычислений со слишком большими знаменателями). После этого, выбрав произвольным
образом рациональное число  , можем вложить многочлены
с целыми
коэффициентами степени не выше
, можем вложить многочлены
с целыми
коэффициентами степени не выше  (рассматриваем случай
(рассматриваем случай  ) в
) в  -мерное пространство над полем
-мерное пространство над полем  , тогда образ
модуля многочленов
образует в этом пространстве решетку размерности
, тогда образ
модуля многочленов
образует в этом пространстве решетку размерности  . Эту решетку
обозначаем
. Эту решетку
обозначаем  . Наша задача заключается в выборе констант
. Наша задача заключается в выборе констант  и
и  таким образом, чтобы
кратчайший вектор этой решетки давал нам неприводимый множитель многочлена
таким образом, чтобы
кратчайший вектор этой решетки давал нам неприводимый множитель многочлена  .
(Квадрат нормы элемента решетки равен сумме квадрата нормы многочлена и
приближенного значения квадрата модуля значения многочлена в
точке
.
(Квадрат нормы элемента решетки равен сумме квадрата нормы многочлена и
приближенного значения квадрата модуля значения многочлена в
точке  ,
умноженного на
,
умноженного на 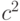 .)
.)
21.2. ПРЕДЛОЖЕНИЕ. Пусть ![g \in \mathbb Z [x]](/sites/default/files/tex_cache/b66170b97a8b090075da5e784495de52.png) - многочлен
степени не выше
- многочлен
степени не выше  , такой,
что
, такой,
что  . Предположим, что
. Предположим, что  и
что
и
что
 |
( 21.9) |
 . Тогда
. Тогда  и
и  .
.ДОКАЗАТЕЛЬСТВО.
Первым делом покажем, что 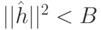 . Так как
. Так как 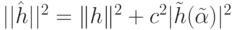 и
и  ,
получаем
,
получаем
 |
( 21.10) |
Оценки на слагаемые:
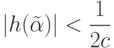 |
( 21.11) |
 |
( 21.12) |
 |
( 21.13) |
оставляются читателю в качестве упражнения.
Доказательство неравенства  .
.
Предполагаем, что 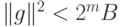 (в противном случае
неравенство очевидно).
Должны доказать, что
(в противном случае
неравенство очевидно).
Должны доказать, что 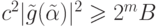 .
Поскольку
.
Поскольку
 |
( 21.14) |
 , то достаточно доказать неравенство
, то достаточно доказать неравенство 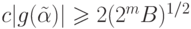 .
.Найдем ![a,b \in \mathbb Z [x]](/sites/default/files/tex_cache/334fca569681064217f75ea768294abe.png) , такие, что
, такие, что  и
и  , и
, и 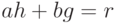 , где
, где  обозначает
результант многочленов
обозначает
результант многочленов  и
и 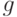 . Из неравенства Адамара (19.3) следует, что
абсолютные значения
коэффициентов
. Из неравенства Адамара (19.3) следует, что
абсолютные значения
коэффициентов  и
и  ограничены величиной
ограничены величиной  , а значит и
, а значит и  . Отсюда, пользуясь тем, что
. Отсюда, пользуясь тем, что  ,
можно получить неравенство
,
можно получить неравенство
 |
( 21.15) |
Отсюда  и
и  .
.
