| Россия, Новосибирск, НГПУ, 1994 |
Программирование, основанное на правилах преобразований
10.2.2. Задание шаблонов с условиями
В предыдущих разделах мы научились задавать правила преобразований и шаблоны для выделения класса выражений, соответствующих значениям гладких математических функций, таких, как правило преобразования, удваивающее квадрат заданного выражения в примере In[1] на рис. 10.5, и шаблон для функций вида xa в примерах на рис. 10.10. Пусть некоторая функция f(x) переменной x принимает значения f1(x) при x<0, значение 0 при x=0 и значения f2(x) при x>0. Для того чтобы задать правило преобразования для такой функции, используют функцию постановки условий Condition. Задаётся эта функция в виде Condition[rppatt,cond], где rppatt — правая часть правила преобразования при условии cond. Так для нашей предполагаемой функции f(x) при условии x<0 правило устанавливается следующим образом: f[x_]:=Condition[f1[x],x<0]. Функция Condition имеет также инфиксную форму " /; ", и задание правила для функции f(x) будет выглядеть как f[x_]:=f1[x]/;x<0. Безусловно, операции сравнения требуют, чтобы участвующие в них выражения были числами.
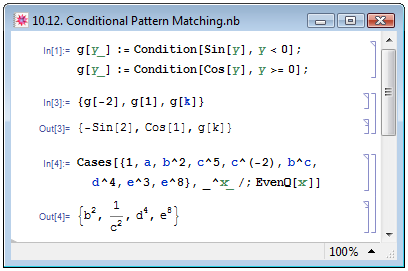
На рис. 10.12 приведено несколько примеров задания правил преобразований с условиями. В In[1] мы отдельно задаём правила преобразования для отрицательных и неотрицательных значениях аргумента. Если аргумент y функции g[y_] примет отрицательное значение (например, -2, как в первом элементе списка In[3]), то будет найден его синус (-Sin[2]), если нулевое или положительное (например, 1) — косинус (Cos[1]). Поскольку для случая, если аргумент y не является числом (k), никаких условий не указано, к выражению никаких правил преобразований применяться не будет, и оно будет переписано в исходном виде с указанным аргументом (g[k]).
В примере In[4] мы выбираем из некоторого списка выражений только те, показатель степени которых чётный. Для этого мы, во-первых, задаём шаблон для выбора выражений со степенью, _^x_, и во-вторых, задаём условие для отфильтровывания нечётных степеней, EvenQ[x].
Подробней о шаблонах с условиями см. книги Е. М. Воробьёва [1, с. 152–153] и П. Веллина и др. [14, с. 156–159].
10.2.3. Задание шаблонов-альтернатив
Если имеется некоторый набор шаблонов, и требуется проверить, соответствует ли то или иное выражение хотя бы одному из них, используются так называемые шаблоны-альтернативы, которые П. Веллин и др. [14, с. 159] определяет как выражения вида patt1|patt2|..., где patt1,patt2,... — независимые шаблоны.
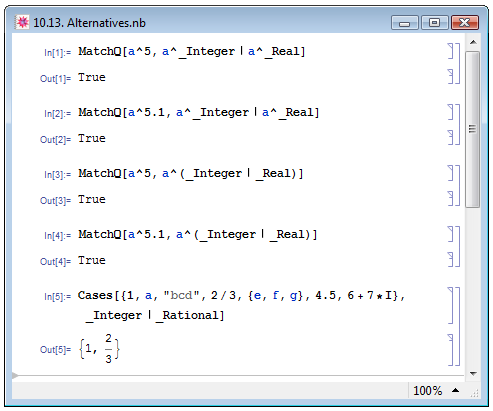
На рис. 10.13 приведём ряд примеров, аналогичных примерам в работе (П. Веллин и др. [14, с. 160]), которые иллюстрируют возможности применения шаблонов-альтернатив. В примере In[1] мы проверяем, представляет ли собой выражение a^5 символ а, возведённый в целочисленную степень либо символ а, возведённый в вещественную степень. Для полноты иллюстрации в In[2] мы проводим такие же манипуляции с выражением a^5.1. В результате обоих вычислений, как и ожидалось, мы получаем True. В примерах In[3] и In[4] мы проверяем те же выражения на соответствие шаблону "символ a, возведённый в целую или вещественную степень", то есть, задаём альтернативу не для полной формы выражения, а только для показателя степени. В примере In[5] из списка разнотипных данных мы выбираем только те элементы, которые являются целыми или рациональными числами.
Подробней о шаблонах-альтернативах см. книгу П. Веллина и др. [14, с. 159–161].
10.2.4. Использование шаблонов в локальных правилах преобразования
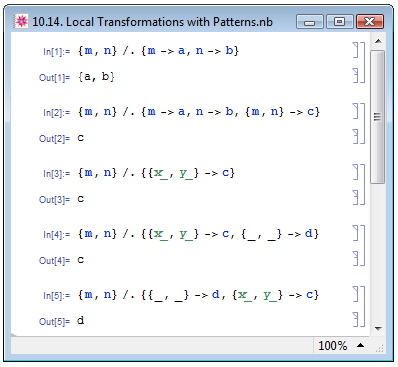
Использование шаблонов в локальных правилах преобразований подробно комметирует Е. М. Воробьёв в своей книге [1, с. 158–162]. Как мы помним из пункта 10.1.2, локальные правила преобразования задаются выражениями вида exprl->expr2 и exprl:>expr2. В настоящем пункте мы научимся задавать локальные правила преобразования, содержащие в выражении expr1 шаблоны. Для этого воспользуемся примером, аналогичным, приведённому в книге Е. М. Воробьёва [1, с. 159–160]. Применим к представляющему собой список выражению {m,n} три разных набора правил подстановки. В примере In[1] на рис. 10.14 зададим правила {m->a,n->b}. Результат преобразований Out[1] достаточно очевиден: m заменено на a, n — на b. В примере In[2] добавим к имеющимся ещё одно правило {m,n}->c. Результирующее выражение Out[2] отличается от Out[1], поскольку последнее правило замены, как оказалось, гораздо больше соответствует преобразуемому выражению.
Теперь попробуем осуществить ту же замену при помощи шаблонов. Для этого в примере In[3] на рис. 10.14 зададим правило замены в виде {x_,y_}->c.
Как мы выяснили в примерах In[1] и In[2] на рис. 10.14, в случае, если к некоторому выражению применено несколько правил преобразования, не содержащих шаблоны, то в первую очередь выполняется то, которое больше соответствует изменяемому выражению. Определим, какое из правил будет выполняться, если они содержат шаблоны. В примере In[4] применим к тому же выражению {m,n} набор правил преобразований {{x_,x_}->c,{_,_}->d}. Хотя исходное выражение соответствует обоим шаблонам, преобразование было выполнено по правилу {x_,x_}->c. В примере In[5] поменяем местами правила преобразований в наборе, т.е., зададим {{_,_}->d,{x_,x_}->c}. Результат в Out[4] показывает, что в данном случае была осуществлена замена по другому правилу, {_,_}->d. Следовательно, если изменяемое выражение соответствует нескольким шаблонам в правилах преобразований, выполняется то правило, которое указано раньше остальных.
Специфическим образом осуществляется вычисление функции многократного применения локальных правил преобразований ReplaceRepeated с шаблонами. Эта специфика доступно пояснена в книге Е. М. Воробьёва [1, с. 160]: "…ее [функции ReplaceRepeated] вычисление сводится к повторному вычислению функции ReplaceAll до тех пор, пока ни одно из подвыражений преобразуемого выражения не удается преобразовать в соответствии с хотя бы одним шаблоном списка. При этом порядок применения шаблонов следующий. Первый шаблон списка используется, пока в преобразуемом выражении находится хотя бы одно подвыражение, ему соответствующее. Затем применяется второй шаблон списка и т.д. Ни в коем случае не следует думать, что каждый раз применяется более чем один шаблон списка".
На рис. 10.15. приведён пример также из книги Е. М. Воробьёва [1, с. 160], иллюстрирующий действие функции ReplaceRepeated. Первый шаблон списка был применён дважды: в результате исходное выражение было сведено к одноэлементному списку {а}. Затем к полученному на предыдущем этапе выражению был применён третий шаблон. Второй шаблон не использовался ни разу, хотя на одном из этапов преобразования и получалось соответствующее ему выражение. После применения третьего шаблона результирующее выражение a оказывается несоответствующим ни одному указанному шаблону, и вычисления прекращаются.
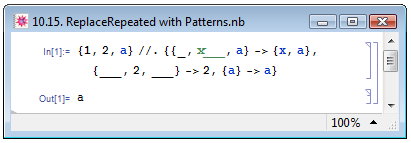
Рис. 10.15. Использование шаблонов при использовании функции многократного применения правил преобразований ReplaceRepeated
Ключевые термины
Верхнее значение выражения — это правило преобразования, ассоциированное с находящимся на первом уровне выражения элементом этого выражения.
Глобальным называется правило преобразования, которое осуществляет заданное преобразование во всём тексте программы.
Локальным называется правило преобразования, которое осуществляет заданное преобразование в отдельном фрагменте программы.
Нижнее значение выражения — это правило преобразования, ассоциированное с заголовком выражения независимо от его элементов на нижних уровнях.
Шаблоном является выражение, содержащее символ подчёркивания (выражение Blanc[]).
Краткие итоги
В данной лекции мы познакомились с принципами программирования на языке Mathematica в стиле, основанном на использовании правил преобразований. В частности мы с новой позиции познакомились с операциями присваивания и отложенного присваивания, выступающими в роли глобальных правил преобразований. Мы научились осуществлять присваивание абсолютно любым выражениям: обходить запрет на присваивание и задавать верхние и нижние значения выражений. Мы познакомились с принципами задания локальных правил преобразований и их использования в вычислениях. Мы научились избирательно обрабатывать выражения в зависимости от их типа и структуры при помощи шаблонов. Также мы научились применять шаблоны при задании глобальных и локальных правил преобразований.