Уравнения. Системы уравнений

8.2. Нахождение численных решений алгебраических и трансцендентных уравнений

Если Mathematica не может в аналитическом виде найти корни уравнений или систем уравнений, например, в случае полиномиальных уравнений 5-го и выше порядков, некоторых трансцендентных уравнений, можно попробовать найти решение численными методами.

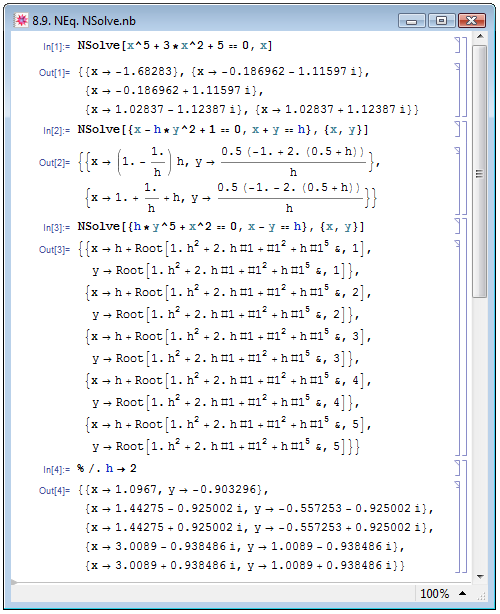
Для численного решения полиномиальных уравнений в Mathematica имеется функция NSolve. Задаётся функция точно так же, как и функция Solve: имеет два обязательных аргумента, первый из которых представляет собой уравнение или систему уравнений, а второй — переменную или перечень переменных. В примере In[1] на рис. 8.9 попробуем численно решить уравнение, которое мы пытались аналитически решить в примере In[2] на рис. 8.2. В Out[1] мы видим, что корни успешно найдены. Безусловно, найти корни уравнение или систему уравнений в явном виде численным методом можно лишь в случае, если все коэффициенты при переменных заданы как численные данные. Если хоть один коэффициент задан в ином виде, например, в символьном, то в решении мы получим либо корни в аналитическом виде (пример In[2]), либо в виде уже знакомых нам Root-объектов (пример In[3]). Как только символьный коэффициент приобретёт численное значение, корни уравнений или системы уравнений сразу могут быть представлены в численном виде (пример In[4]).

Подробней о функции NSolve см. книгу А. Н. Прокопени и А. В. Чичурина [5, с. 18–19].

Рис. 8.9. Нахождение численных решений алгебраических уравнений при помощи функции NSolve

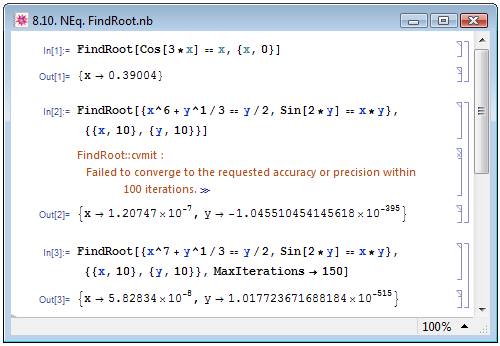
Функция NSolve эффективно работает с полиномиальными уравнениями и системами уравнений. Если же уравнения содержат более замысловатые математические функции, то какой-то специальной процедуры нахождения всех решений даже численными методами не существует. В этом случае используется функция FindRoot: но она находит только один корень. В общем виде функция задаётся как FindRoot[{eqn1,eqn2,...},{{var1,varstart1},{var2,varstart2},...}], где eqn1,eqn2,... — система уравнений, var1,var2,...— переменные, varstart1,varstart2,... — начальное приближение к решению, от которого Mathematica начинает поиск истинного решения. В примере In[1] на рис. 8.10 при помощи функции FindRoot мы нашли корень уравнения из In[2] на рис. 8.3, которое не смогли решить аналитически.

Функция FindRoot также может представлять результат вычисления в виде Root-объектов.

Для нахождения корня уравнения или системы уравнений функция FindRoot проводит поиск итерационным методом касательных, с каждой итерацией приближаясь к истинному значению корня. Заданное по умолчанию число итераций равняется 100. Однако для некоторых уравнений, а также в зависимости от заданной нами начальной точки поиска этого числа не хватает для достаточно точного, по мнению Mathematica, нахождения корней (пример In[2] на рис. 8.10). Иное число итераций можно задать при помощи опции MaxIterations (пример In[3] на рис. 8.10).

О функции FindRoot см. книгу А. Н. Прокопени и А. В. Чичурина [5, с. 19–20].

Рис. 8.10. Нахождение корня уравнения при помощи функции FindRoot

Как мы видим из сказанного выше, возможности Mathematica в решении уравнений небезграничны. Даже численными методами для некоторых уравнений одномоментно можно найти только один корень. Пользуясь для этого функцией FindRoot, следует из некоторых соображений самостоятельно вручную задавать точку для начала поиска корней. А некоторые уравнения и вовсе могут не иметь корней, и для их нахождения будет впустую потрачено машинное время и ресурсы. Чтобы при проведении расчётов хоть как-то гарантировать нахождение корня при их наличии или сэкономить силы и время, не тратя их на поиски корней, если их вовсе нет, прибегают к мощнейшему средству Mathematica для представления данных — графике. Графическому решению уравнений много внимания уделено в книге В. П. Дьяконова [2, с. 258–262]. В настоящем курсе мы познакомимся с сутью и основными принципами этого метода.

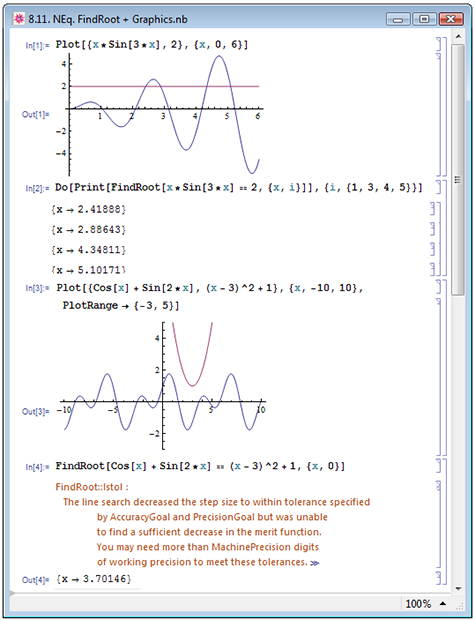
Пусть мы хотим найти решение трансцендентного уравнения , причём нас интересуют только x, принадлежащие отрезку от 0 до 6. Для этого сначала мы строим на одном графике левую и правую части уравнения в зависимости от x в указанных пределах при помощи функции Plot (пример In[1] на рис. 8.11). Как видно на рисунке в Out[2], графики имеют 4 пересечения, а уравнение, соответственно, 4 корня, причём приблизительное положение этих корней мы также можем определить из графика. Теперь, задавая эти приблизительные координаты в качестве исходных точек для нахождения корней, мы находим сами корни при помощи функции FindRoot — см. пример In[2]. В данном примере, используя цикл Do (с циклами мы познакомимся в лекции настоящего курса, посвящённой процедурному программированию), мы выводили на экран при помощи функции Print результат выполнения функции FindRoot, меняя каждый раз значение исходной точки поиска i.

Приведём ещё один пример. Пусть у нас возникла необходимость решить уравнение относительно x из отрезка от -10 до 10. Действуем по тому же алгоритму. Сначала визуализируем тригонометрическую и параболическую 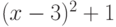зависимости от переменной x (пример In[3] на рис. 8.11). Как мы видим на рисунке в Out[3], кривые не имеют ни одного пересечения в интересующей нас области и, ввиду периодичности первой функции и принципиального нахождения выше уровня 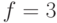второй, они не имеют пересечений вовсе. Соответственно, и уравнение не будет иметь корней: искать их не имеет смысла. Если же мы всё же попытаемся найти корни уравнения при помощи функции FindRoot (пример In[4]), Mathematica выдаст сообщение о том, что при заданных значениях точности и разрядности не может найти удовлетворительного решения и рекомендует повысить точность вычислений (хотя, мы уже знаем, что никакого результата это не даст).

увеличить изображение
Рис. 8.11. Применение графических средств для нахождения корней уравнений численными методами