|
есть желание заново пройти курс "Тестирование в современном высшем образовании"
|
Обоснование качества теста
5.5. Какие задачи оценки качества обучения можно решать еще?
Разумеется, их множество. И они бывают весьма непростые. Но приводим лишь несколько, "просто полезные примеры".
Пример. Пусть имеется база из N заданий, из которых формируется тест длины n случайной выборкой заданий. Необходимо адаптивно перейти на новый уровень, если обучаемый дал на них m правильных ответов при необходимых для перехода М ответах, оценивая вероятности успешного ответа обучаемых.
Вероятность того, что обучаемый сможет ответить, равна:
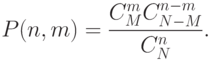
Простая оценка:
![S^2(\tau)=\frac{n}{n-1}\left[\frac{1}{n}\sum_{i=1}^{n}\tau^2_i-(\frac{1}{n}\sum_{i=1}^{n}\tau_i)2\right],](/sites/default/files/tex_cache/1a1edfb9024a0ec160f9789b6b4a2ab3.png)
где 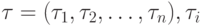 – время выполнения задания в i–ой попытке,
– время выполнения задания в i–ой попытке,  - вектор теста, n – количество попыток.
- вектор теста, n – количество попыток.
Пример. Разработчик теста разбил тест С на два субтеста А и В (создал две идентичные формы теста Т). Если А и В строго идентичны (параллельны), то коэффициент надежности для любой формы будет 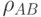 . Предположим, что предъявляются обе формы Т и необходимо вычислить общую оценку по каждому испытуемому.
. Предположим, что предъявляются обе формы Т и необходимо вычислить общую оценку по каждому испытуемому.
Составная оценка – это общая оценка, основанная на двух или более оценках по субтестам. Она основана на составной оценке:
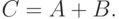
Как определить надежность составных оценок? Разработчику теста следует создать опять две формы субтестов для получения составной оцен-ки. Но какова надежность такой (составной) оценки по четырем субтестам?
Построить метод выяснения надежности составной оценки по статистическим свойствам ее компонентов можно, используя прогнозную процедуру Спирмана-Брауна, которая позволяет оценить надежность составной оценки по параллельным тестам, если надежность одного из них известна.
Пример. Необходимо выявить эффективно общую тенденцию в случайных данных, например, выявить степень обученности по результатам, выбираемым случайным образом. Эффективным методом (приемом) выявления общей тенденции динамики в случайных данных является аналитическое выравнивание, используя различные формы зависимости.
Если динамический ряд уровня знаний соответствует процессу со стабильным абсолютным приростом знаний, то подходящим уравнением будет y(t)=a0+a1t, где a0 и a1 – параметры уравнения, t – время. Параметр a1 (коэффициент углового наклона) определяет направление развития. Если a1>0, то уровни ряда динамики равномерно возрастают, а при a1< 0 – равномерно снижаются. Основная тенденция развития во временных рядах со стабильными темпами прироста отображается квадратичной функцией y(t)=a0+a1t+a2t2. Параметр a2 характеризует постоянное изменение интенсивности развития (в единицу времени). При a2>0 происходит ускорение развития, а при а2<0 – замедление.
Основная тенденция во временных рядах с постоянными темпами роста отображается показательной функцией y(t)=a0a1t, где а1 – темп роста (снижения) изучаемого явления в единицу времени, т.е. интенсивность развития.

