НОУ ИНТУИТ | Тестирование в современном высшем образовании. Лекция 5: Обоснование качества теста

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 30.11.2014 | Уровень: для всех | Доступ: платный | ВУЗ: Кабардино-Балкарский государственный университет

|

Вам нравится? Нравится 27 студентам

| Поделиться |

Поддержать программу

5.2. Задачи и алгоритмы оценки

Рассмотрим некоторые базовые понятия и задачи (алгоритмы) проведения оценивания по любой методологии. Сам класс таких задач – весьма широк.

Задача 1. Пусть даны результаты тестирования группы, состоящей из n испытуемых для заданного теста из m различных знаний. Обычно эти данные представляются в виде некоторой матрицы A баллов размерности n на m:

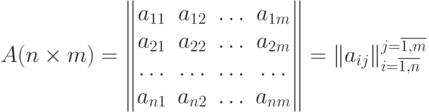
$A(n\times m)=\begin{Vmatrix}a_{11}&a_{12}&\dots&a_{1m}\\a_{21}&a_{22}&\dots&a_{2m}\\\dots&\dots&\dots&\dots\\a_{n1}&a_{n2}&\dots&a_{nm}\\\end{Vmatrix}=\|a_{ij}\|_{i=\overline{1,n}}^{j=\overline{1,m}}$

Элемент a^ij матрицы A представляет собой результат выполнения j-го задания для i-го тестируемого.

Необходимо на основе имеющихся результатов x¹, x², ..., xⁿ тестирования для каждого из n тестированных, вычислить основные статистические показатели тестирования (оценить "сырые" результаты) для выбранной случайным образом группы тестированных.

Алгоритм решения этой задачи состоит из следующих этапов.

Упорядочиваем ряд по возрастанию (находим генеральную совокупность): x₁<x₂<...> x_n.
Выбираем интересующее нас подмножество тестированных (выборку).
Находим среднее арифметическое по выборке
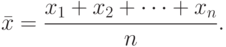
$\bar x=\frac{x_1+x_2+\cdots+x_n}{n}.$
Находим величины, характеризующие структурные изменения, например, моду и медиану. Для данных, имеющих "хорошее поведение", медиана всегда лежит в промежутке между средним арифметическим и модой. Эти величины выстраиваются по возрастанию следующим образом: среднее, медиана, мода, или же в обратном порядке. Прямой или обратный порядок их расположения можно определить, вычислив так называемый коэффициент асимметрии:
$K=\frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar x)^3}{(\sqrt{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar x)^2})^3}.$
Этот коэффициент отражает относительную изменчивость данных.
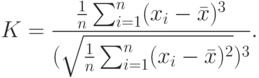
Находим меры рассеяния, разброса или вариации, показывающие, как остальные элементы совокупности (выборки) группируются около средних величин. Например,
1. размах
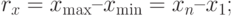
  $r_x=x_{\max} – x_{\min} = x_n – x_1;$
2. среднее абсолютное отклонение
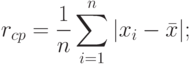
  $r_{cp}=\frac{1}{n}\sum_{i=1}^{n}|x_i-\bar x|;$
3. среднеквадратичное отклонение
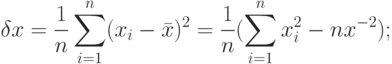
  $\delta x=\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar x)^2=\frac{1}{n}(\sum_{i=1}^{n}x_i^2-n x^{-2});$
4. дисперсия
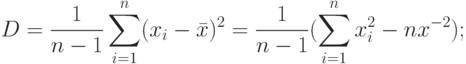
  $D=\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar x)^2=\frac{1}{n-1}(\sum_{i=1}^{n}x_i^2-n x^{-2});$
5. стандартное отклонение:
  $\sigma=\sqrt{D};$
6. коэффициент вариации
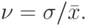
  $\nu=\sigma/\bar x.$
Конец алгоритма.

Задача 2. Даны результаты тестирования для каждого из n тестированных и теста длины m в виде матрицы A, а также вектор эталонных ответов B=(b₁, b₂, …, b_m), где b_j – эталонный ответ на задание номер j. Необходимо определить "вес" (меру сложности) конкретного задания теста.

Простейший алгоритм решения этой задачи состоит из следующих этапов.

Определяем для очередного задания теста по матрице А количество тестированных, давших правильный ответ на данное задание.
В качестве "веса" задания берется дробь c_j: знаменатель – количество тестированных, числитель – количество тестированных, давших правильные ответы на все задания.
Вычисляем смежные веса d_i: знаменатель – количество всех тестированных, давших неправильный ответ на данное задание номер j, числитель – количество тестированных, давших неправильные ответы на все задания. Иногда в знаменателе берется количество всех тестированных.
Находится вектор весов выполнения c=(c₁, c₂, …, c_m) для заданного вектора b эталонных ответов.
Находим вектор весов невыполнения d=(d₁, d₂, …, d_m) для заданного вектора b эталонных ответов.
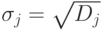Оцениваем дисперсию каждого j-го задания D_j=с_id_i и стандартное отклонение $\sigma_j=\sqrt{D_j}$ .
Конец алгоритма.

Задача 3. Даны результаты тестирования для каждого из n тестированных и теста длины m в виде матрицы A, а также вектор эталонных ответов B=(b₁, b₂, …, b_m), где b_j – эталонный ответ на задание номер j. Необходимо оценить валидность каждого задания теста.

Простейший алгоритм решения этой задачи состоит из следующих этапов.

Определяем для очередного задания теста по матрице A количество тестированных, давших правильный ответ на j-ое задание и находим их средний балл x_j.
Находим аналогично количество тестированных, давших неправильный ответ на j-ое задание и их средний балл y_j.
Находим дробь c_j: знаменатель – количество тестированных, давших правильный ответ на данное задание номер j, числитель – количество тестированных.
Находим дробь d_i: знаменатель – количество тестированных, давших неправильный ответ на данное задание номер j, числитель – количество тестированных.
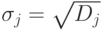Оцениваем дисперсию каждого j-го задания D_j=с_id_i и стандартное отклонение $\sigma_j=\sqrt{D_j}$ .
Находим стандартное отклонение 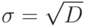$\sigma=\sqrt{D}$ по всему тесту.
Находим коэффициент корреляции (меру валидности задания):
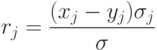
$r_j = \frac {(x_j-y_j)\sigma_j}{\sigma}$
Если r_j>0,3, то задание считаем валидным, иначе – не валидным (с точки зрения критериальной валидности, задания, выполненные всеми или невыполненные никем, не являются валидными).
Конец алгоритма.

Задача 4. Даны результаты нормативно-ориентированного тестирования для каждого из n тестированных и теста длины m в виде матрицы A, а также вектор эталонных ответов B=(b₁, b₂, …, b_m), где b_j – эталонный ответ на задание номер j. Необходимо оценить надежность теста (степень устойчивости результатов тестирования каждого испытуемого, если тестирование было проведено в совершенно одинаковых условиях).

Для вычисления надежности нормативно-ориентированного теста используем коэффициент корреляции между результатами двух параллельных тестов. Сравнивая коэффициенты корреляции, делаем заключение о надежности (внутренней) теста. Если две половины теста коррелированы, то и тест надёжен; в противном случае – не надёжен (или необходимо применить другой, более тонкий математический аппарат исследования надежности).

Простой алгоритм решения этой задачи состоит из следующих этапов.

Делим тест на две равные части X и Y, например, по четным и нечетным номерам заданий. Этот метод называется методом расщепления теста. Таким образом, мы имеем данные по двум параллельным тестам X и Y – индивидуальные баллы (x₁, x₂, …, x_n), (y₁, y₂, …, y_n), где n – количество тестированных.
Для каждого задания группы X выполняем предыдущий алгоритм.
Для каждого задания группы Y выполняем предыдущий алгоритм.
Находим коэффициент корреляции X и Y по формуле:
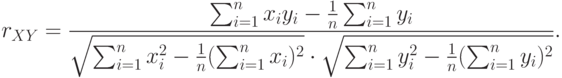
$r_{XY}=\frac{\sum_{i=1}^{n}x_iy_i-\frac{1}{n}\sum_{i=1}^{n}y_i}{\sqrt{\sum_{i=1}^{n}x_i^2-\frac{1}{n}(\sum_{i=1}^{n}x_i)^2}\cdot\sqrt{\sum_{i=1}^{n}y_i^2-\frac{1}{n}(\sum_{i=1}^{n}y_i)^2}}.$
Находим надежность r всего теста по формуле (Спирмена-Брауна):
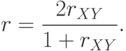
$r=\frac{2r_{XY}}{1+r_{XY}}.$
Конец алгоритма.

Задача 5. Необходимо на основе имеющихся результатов тестирования (матрица А) получить для каждого из n тестированных интегральный (обобщенный) показатель выполнения теста длины m, а затем по вычисленным значениям этого интегрального показателя разбить всех тестированных на заданное количество k групп.

Алгоритм решения этой задачи состоит из следующих этапов.

Если для j-го задания увеличение значений результатов измерения свидетельствует об улучшении соответствующего свойства, то с ним свяжем признак z_j=1, а если свидетельствует об ухудшении – признак z_j=–1.
Выполняем нормирование элементов исходной матрицы так, чтобы в каждом столбце они изменялись в "одном направлении": для каждого задания (при фиксированном j=1, 2, …, m) и для каждого испытуемого i=1, 2, …, n вычислим новое значение
$a_{ij}:=\frac{a_{ij}-m_j}{M_j-m_j},$
где M_j, m_j – наибольшее и наименьшее значения элементов j-го столбца и применяем преобразование вида
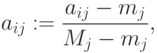
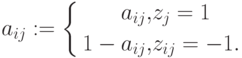
$a_{ij}:=\left\{\begin{aligned}a_{ij},&z_j=1\\1-a_{ij},&z_{ij}=-1.\\\end{aligned}\right.$
Для каждого столбца полученной новой матрицы А (нормированной) вычисляется среднее квадратичное отклонение по формуле
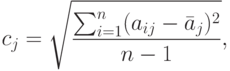
$c_{j}=\sqrt{\frac{\sum_{i=1}^{n}(a_{ij}-\bar a_j)^2}{n-1}},$
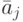где $\bar a_j$ – среднее арифметическое элементов j-го столбца.
Вычисляется классификационный интегральный показатель
$y_i=\sum_{j=1}^{m}a_{ij}c_i,$
где y_i – значение интегрального показателя для i-го обучаемого i=(1,2,…,n), c_j – весовой коэффициент j-го задания в тесте или в банке всех заданий, a _ij– элемент матрицы А или его преобразованное (нормированное, например, по отношению к максимальному элементу или к норме матрицы).
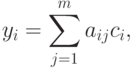
Находим наименьшее y_min и y_max наибольшее значения интегрального показателя (по всем тестированным). Отрезок [y_miny_max;] делим на заданное число k интервалов. Часто берут (при построении, например, гистограммы) k=1+3,2lgn. Всех тестированных, для которых вычисленные значения интегрального показателя попадают в один и тот же интервал, отождествляем и относим к одному классу.
Выдаем результаты: значения интегрального показателя для каждого тестированного, а также его класс (или классификацию тестированных по интегральному показателю).
Конец алгоритма.

Задача 6. Есть результаты тестирования, полученные в виде матрицы А. Необходимо разбить всех тестированных на несколько групп по отношению к норме (сильные, средние, слабые), где величина x – норма для тестовых результатов и величина k – масштабный коэффициент.

Алгоритм решения задачи.

Ввод данных: n, m, A, k.
Для каждого из тестированных определяем его суммарный балл:
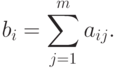
$b_i=\sum_{j=1}^{m}a_{ij}.$
Разбиваем рассматриваемую выборку тестированных на 3 группы. В первую группу попадают с высокими баллами: суммарный балл для попадающих в эту группу не ниже значения выражения
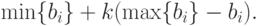
$\min\{b_i\}+k(\max\{b_i\}-b_i).$
В третью группу попадают с низкими баллами – не выше значения выражения
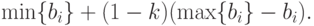
$\min\{b_i\}+(1-k)(\max\{b_i\}-b_i).$
Во вторую группу попадают все остальные (со средними баллами).
Выдача результатов: количество и состав попавших в каждую группу.
Конец алгоритма.

Задача 7. Необходимо отсеять первичные ("сырые") результаты в группах, т.е. по данным x₁, x₂, …, x_n (процент выполнения, валидность и т.д.) выяснить задания (тесты, результаты), которые не согласуются с общей картиной тестирования.

Алгоритм решения задачи состоит из следующих этапов.

Вычисляется средняя величина $\bar x.$
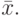
Вычисляются наибольшее x_max и наименьшее x_min в группе.
Вычисляются наибольшее отклонение в группе:
$d_{\max}=|x_{\min(\max)}-\bar x|.$
Вычисляется относительное отклонение:
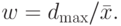
$w=d_{\max}/\bar x.$
Находим по таблице распределения Стьюдента процентные точки для t(5%) и t(0.1%). Таблица Стьюдента имеется практически во всех справочниках по математической статистике и в математических пакетах.
Вычисляем соответствующие точки w(5%;n), w(0.1%;n).
Если
$w(5\%;n)>t(5\%) (w(0.1\%;n)>t(0.1\%)),$
то отсеиваем рассматриваемое данное и пересчитываем все заново (повторяем заново пункты 1-6).
Конец алгоритма.