Графы в компьютерной геометрии

Графы и связанные с ними задачи

Определение 7.1.1. Графом называется пара G = (V,E) , где V - некоторое конечное множество, элементы которого называются вершинами, а E - семейство неупорядоченных пар (двухэлементных подмножеств) множества V, называемых ребрами. Если пара вершин v и w составляет ребро e = vw, то говорят, что эти вершины смежные или соседние. Также в этом случае говорят, что ребро e и вершина v инцидентны. Наконец, ребра, пересекающиеся по вершине, также называют смежными или соседними.

Замечание 7.1.1. Графы, которые мы только что определили, часто называют простыми. Аналогично определяются ориентированные графы (ребра - упорядоченные пары вершин) и мультиграфы (допускаются петли и кратные, т. е. соединяющие одни и те же вершины, ребра).

Граф G = (V,E) называется взвешенным, если на множестве его ребер задана весовая функция 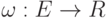, которая обычно предполагается неотрицательной.

Красивое изображение графов в пакете Mathematica

Для продуктивной работы с графами часто требуется визуализировать граф наиболее наглядным образом. Особенно эта проблема важна в случае больших графов. В пакете Mathematica имеется ряд встроенных функций рисования графов на плоскости или в трехмерном пространстве, при котором расположение вершин и форма ребер вычисляется так, чтобы оптимизировать тот или иной "эстетический" функционал.

Перечислим основные функции, используемые в пакете Mathematica для изображения графов, и приведем примеры их использования. Стандартная функция строит изображение мультиграфа, при котором вершина 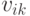соединяется ребром с вершиной :

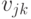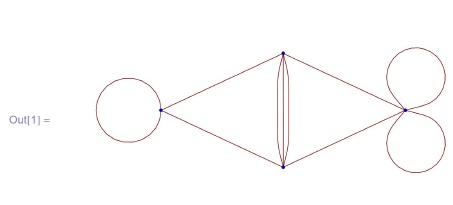
In[1]:= GraphPlot [{1 -> 2, 1 -> 2, 2 -> 1, 3 -> 3,
                3 -> 1, 3 -> 2, 4 -> 1, 4 -> 2, 4 -> 4, 4 -> 4}]

При наведении курсора мыши на вершины графа возникают номера этих вершин. Заметьте, что пары {1, 2} встречаются три раза, - это изображено ребром кратности три. Кроме того, имеются петли, заданные двумя парами (4,4) и одной парой (3,3).

Вообще говоря, такое представление естественно для ориентированного графа, хотя приведенное выше изображение игнорировало этот факт. Визуализацию направления ребер можно включить следующей опцией:

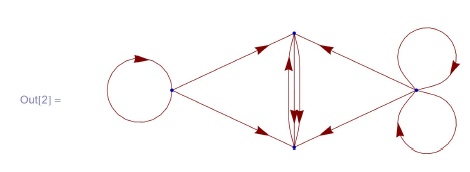
In[2] := GraphPlot [{1 -> 2, 1 -> 2, 2 -> 1, 3 -> 3,
                 3 -> 1, 3 -> 2, 4 -> 1, 4 -> 2, 4 -> 4, 4 -> 4}, 
               DirectedEdges -> True]

Вот еще два формата команды GraphPlot:

приписывает ребр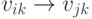у метку :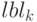

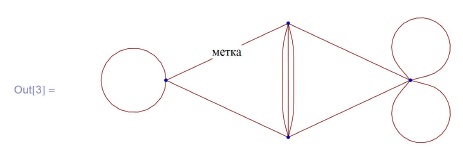
In[3]:= GraphPlot[{1 -> 2, 1 -> 2, 2 -> 1, 3 -> 3,
             {3 -> 1, "метка"}, 3 -> 2, 4 -> 1, 4 -> 2, 
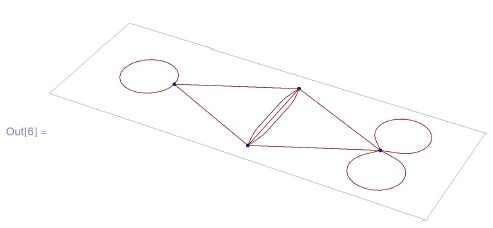
               4 -> 4, 4 -> 4}]

GraphPlot[m] строит граф по матрице вершинной смежности, в которой на (i,j)-м месте стоит кратность ребра, идущего из вершины с номером i в вершину с номером j (если ребра нет, то кратность равна нулю). Заметим, что теперь для визуализации петель и кратных ребер нужно специально включать соответствующие опции SelfLoopStyle и MultiedgeStyle, которые по умолчанию выключены.

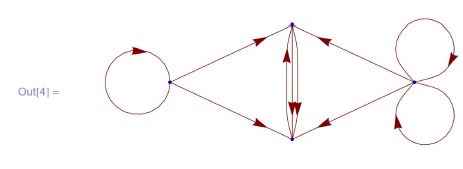
In[4]:= GraphPlot [{{0, 2, 0, 0}, {1, 0, 0, 0}, {1, 1, 1, 0}, 
               {1, 1, 0, 2}}, DirectedEdges -> True, 
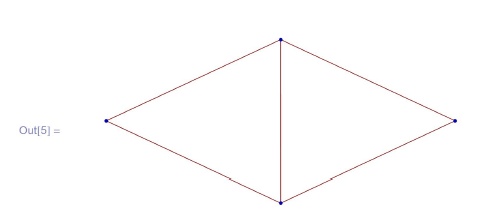
            SelfLoopStyle -> True, MultiedgeStyle -> True]

In[5]:= GraphPlot [{{0, 2, 0, 0}, {1, 0, 0, 0}, 
            {1, 1, 1, 0}, {1, 1, 0, 2}}]

У команды GraphPlot[m] имеется много опций, с которыми можно ознакомиться, нажав кнопку MORE INFORMATION из Help для GraphPlot.

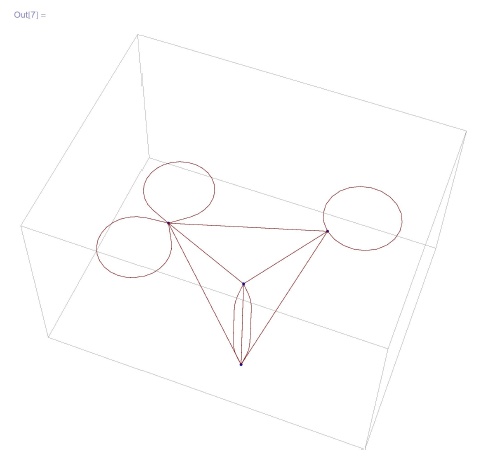
Команда GraphPlot3D имеет такой же формат, как и GraphPlot, однако изображает графы в трехмерном пространстве.

In[6] :=GraphPlot3D[{l -> 2, 1 -> 2, 2 -> 1, 3 -> 3,
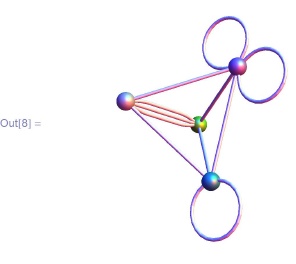
            3 -> 1, 3 -> 2, 4 -> 1, 4 -> 2, 4 -> 4, 4 -> 4}]

In[7]:=GraphPlot3D[{l -> 2, 1 -> 2, 2 -> 1, 3 -> 3,
        3 -> 1, 3 -> 2, 3 -> 4, 4 -> 1, 4 -> 2, 4 -> 4, 4 -> 4}]

А вот пример более симпатичного изображения графа. Здесь опция EdgeRenderingFunction определяет функцию прорисовки ребра (в примере рисуется трубка Tube, ось которой задается последовательными точками ребра, возвращаемыми GraphPlot3D в первый аргумент #1 этой функции, 0.015 - радиус трубки), опция VertexRenderingFunction - функцию прорисовки вершин (они изображаются сферами):

In[8]:=GraphPlot3D[{l -> 2, 1 -> 2, 2 -> 1, 3 -> 3, 
             3 -> 1, 3 -> 2, 3 -> 4, 4 -> 1, 4 -> 2, 
             4 -> 4, 4 -> 4}, SelfLoopStyle -> True, 
          MultiedgeStyle -> True,
          EdgeRenderingFunction -> (Tube[#2, 0.015] &) , 
          VertexRenderingFunction -> ({ColorData["Atoms"]
                [RandomInteger[{l, 117}]], Sphere[#2, .08]} &) , 
          PlotStyle -> Directive[Specularity[White, 20] ] , 
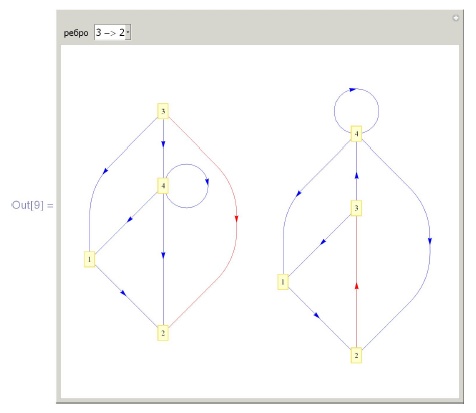
          Boxed -> False]

Функция LayeredGraphPlot относится к так называемому иерархическому рисованию и изображает ориентированный граф, располагая вершины на уровнях так, чтобы доминантные вершины (те, в которые входит как можно меньше стрелочек) оказались наверху, а стрелочки были направлены преимущественно вниз. Ниже приведена программа, демонстрирующая, как меняется вид графа при изменении направления ровно одного ребра.

In[9] :=
      DynamicModule[{v, w, edge}, 
        v ={1 -> 2, 3 -> 1, 3 -> 2, 3 -> 4, 4 -> 1, 4 -> 2, 4 -> 4}; vv= v; 
        Manipulate[  
           If [ls ≠ "None", edge = List @@ ToExpression[ls] ; 
             vv = v / . Rule @@ edge -> Rule @@ (RotateLef t [edge]) ] ;  
           Row[{LayeredGraphPlot[v, VertexLabeling -> True,  
               EdgeRenderingFunction ->  
                    (If[(ls ≠ "None") && (# == edge) , {Red, Arrowheads[{{Automatic, 0.5}}] ,  
                         Arrow[#2]}, {Blue, Arrowheads[{{Automatic, 0.5}}], Arrow[#1]}] &) , 
                 ImageSize -> 250] ,  
               LayeredGraphPlot[vv, VertexLabeling -> True, ImageSize -> 250,  
                 EdgeRenderingFunction ->  
                    (If [(ls ≠ "None") && (#2 == RotateLeft[edge]) , 
                         {Red, Arrowheads [{ {Automatic , 0.5}}], Arrow[#l]}, 
                         {Blue, Arrowheads[{{Automatic, 0.5}}], Arrow[#1]}] &)]},"  " ] , 
        {{ls, "None", "ребро"}, { "None" } ≈ Join ≈ (ToString/@ v) } ] , 
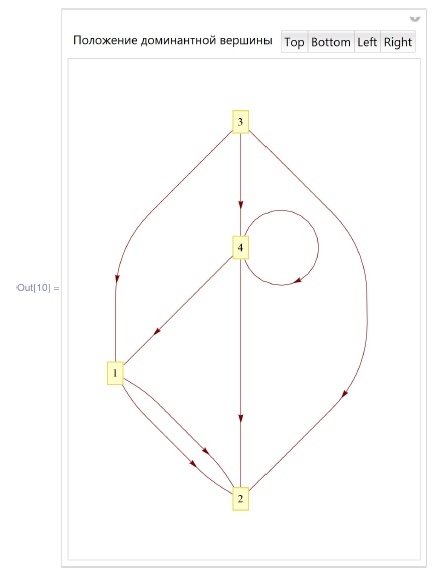
      UnsavedVariables -> {vv, edge}]

Отметим, что у функции LayeredGraphPlot имеется еще один формат, а именно, LayeredGraphPlot[g,pos] , позволяющий задавать, с какой стороны располагать доминантные вершины. Возможные значения для pos -это Right, Left, Top и Bottom:

In[10] := Manipulate [
               LayeredGraphPlot[ 
                  {1 -> 2, 1 -> 2, 3 -> 1, 3 -> 2, 3 -> 4, 4 -> 1,
                    4 -> 2, 4 -> 4}, 
                  pos, 
                  VertexLabeling -> True] ,
               {
                 {pos, "Top", "Положение доминантной вершины"},
                 {Top, Bottom, Left, Right}
               }
            ]

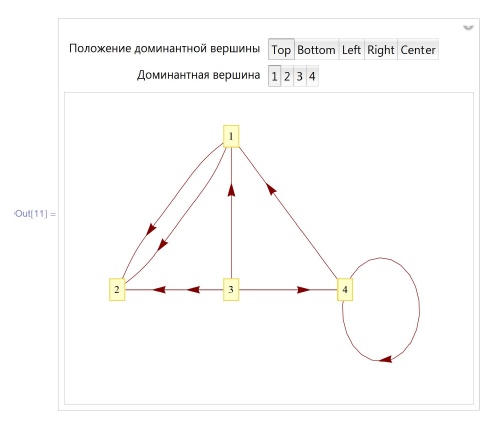
Еще одна иерархическая функция изображения графов - это TreePlot. Несмотря на название, она применима не только к деревьям, но и к графам общего вида (в качестве деревьев у графов берутся остовные деревья их связных компонент, определения см. ниже). Ребра, не являющиеся петлями и кратными ребрами, изображаются отрезками, что может приводить к совмещению некоторых ребер (см. пример ниже). По своим форматам эта функция похожа на LayeredGraphPlot, однако она имеет дополнительный формат TreePlot[g,pos,v_k] , в котором обозначает вершину, которую нужно выбрать в качестве корня. Кроме того, pos может принимать еще и значение Center:

In[11] :=Manipulate[TreePlot[{l -< 2, 1 -< 2, 3 -< 1, 
              3 -> 2, 3 -> 4, 4 -> 1, 4 -> 2, 4 -> 4}, 
           pos, root, VertexLabeling -> True,
           DirectedEdges -> True], 
       {{pos, Top, "Положение доминантной вершины"},
         {Top, Bottom, Left, Right, Center}}, 
       {{root, 1, "Доминантная вершина"}, {1, 2, 3, 4}}, 
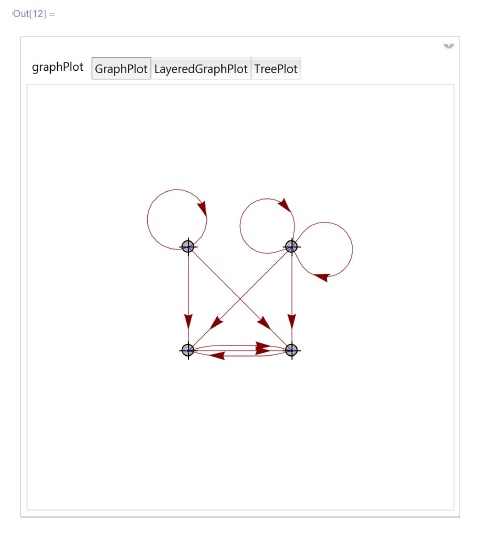
       ControlPlacement -> Top]

У всех перечисленных выше функций рисования графов имеется полезная для решения геометрических задач опция VertexCoordinateRules, позволяющая явно указывать координаты вершин графа. Координаты можно задавать или в виде списка, или явно указывать, какой вершине какие координаты приписать, т. е. 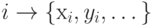. Также вместо некоторых координат может стоять Automatic:

In[12] :=
   Manipulate[ 
      graphPlot[{l -> 2, 1 -> 2, 2 -> 1, 3 -> 3, 3 -> 1, 
            3 -> 2, 4 -> 1, 4 -> 2, 4 -> 4, 4 -> 4}, 
          VertexCoordinateRules -> p, PlotRange -> { {-1, 2}, {-1, 2}}, 
        AspectRatio -> Automatic, DirectedEdges -> True] , 
     {{P, {{0, 0}, {1, 0}, {0, 1}, {1, 1}}}, Locator}, 
     {graphPlot, {GraphPlot, LayeredGraphPlot, TreePlot}}]

In[13] : =
    DynamicModule[ {p0 , pp, plnit}, 
         p0 = {{0, 0}, {1, 0}, {0, 1}, {1, 1}}; 
         pInit = p0|[Drop [Range [4] , {1}]]];
         Manipulate [plnit = pO[[Drop [Range [4] , {automatic} ] ]] ; 
             pp = Maplndexed[First[#2] -> #1 &,
                Insert[p, {Automatic, Automatic}, automatic]]; 
            Quiet@graphPlot[{l -> 2, 1 -> 2, 2 -> 1, 3 -> 3,
                   3 -> 1, 3 -> 2, 4 -> 1, 4 -> 2, 4 -> 4, 4 -> 4}, 
                VertexCoordinateRules -> pp, PlotRange -> {{-1, 2}, {-1, 2}}, 
                AspectRatio -> Automatic, DirectedEdges -> True] , 
           {{p, plnit}, Locator},
           {graphPlot, {GraphPlot, LayeredGraphPlot, TreePlot}}, 
           {{automatic, 1, "Вершина, позиционируемая автоматически"}, 
             {1, 2, 3, 4}}], UnsavedVariables -> {pp, plnit} 
]