Графы в компьютерной геометрии
Пример оптимизационной задачи: задача о минимальном остовном дереве
Связный граф без циклов называется деревом. Понятие дерева играет важную роль в приложениях, поскольку моделирует такой вид соединения своих вершин, в котором "нет ничего лишнего".
Подграфом H в графе 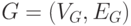 называется такой граф
называется такой граф  , что
, что  и
и  . Если граф G - взвешенный с весовой функцией
. Если граф G - взвешенный с весовой функцией 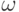 , то для каждого его подграфа H естественно определяется его вес, равный сумме весов всех ребер этого подграфа.
, то для каждого его подграфа H естественно определяется его вес, равный сумме весов всех ребер этого подграфа.
Подграф 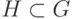 называется остовным, если
называется остовным, если 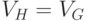 . В каждом связном графе, очевидно, имеется остовный подграф, являющийся деревом. Такие подграфы называются остовными деревьями. Количество разных остовных деревьев зависит от структуры графа. Для простого связного графа оно может быть вычислено с помощью так называемой матричной теоремы Кирхгофа. Интересующая нас точная оценка сверху имеет вид
. В каждом связном графе, очевидно, имеется остовный подграф, являющийся деревом. Такие подграфы называются остовными деревьями. Количество разных остовных деревьев зависит от структуры графа. Для простого связного графа оно может быть вычислено с помощью так называемой матричной теоремы Кирхгофа. Интересующая нас точная оценка сверху имеет вид 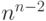 , где
, где  - количество вершин графа.
- количество вершин графа.
Остовное дерево наименьшего веса в связном взвешенном графе называется минимальным остовным деревом Несмотря на упомянутую оценку, имеются полиномиальные алгоритмы построения минимальных остовных деревьев. Одним из таких алгоритмов является алгоритм Краскала.
Пусть G = (V,E) - связный взвешенный граф с весовой функцией 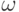 . Определим граф
. Определим граф 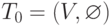 . На
. На  -м шаге,
-м шаге,  , среди всех ребер, добавление которых к
, среди всех ребер, добавление которых к 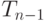 порождает ацикличный граф, выберем ребро наименьшего веса и добавим к
порождает ацикличный граф, выберем ребро наименьшего веса и добавим к 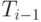 получив тем самым
получив тем самым 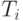 . Алгоритм заканчивает работу, построив граф
. Алгоритм заканчивает работу, построив граф 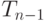 , который и является минимальным остовным деревом.
, который и является минимальным остовным деревом.
В пакете Combinatorica имеется команда MinimumSpanningTree[<граф>], возвращающая минимальное остовное дерево в формате Graph.
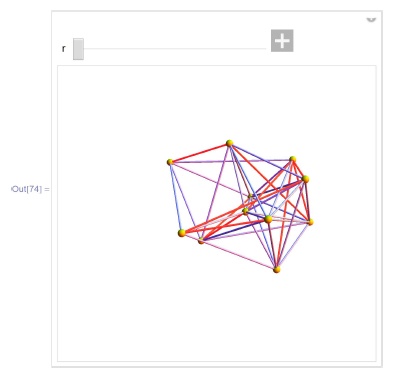
Снова нарисуем красивые картинки:
In[74] :=
DynamicModule[{gu, gcur, mst, n = 11},
gu = RandomGraph[n, . 6] ;
While [! ConnectedQ[gu], gu = RandomGraph[n, . 6] ] ;
gcur = SetEdgeWeights[gu];
mst = MinimumSpanningTree[gcur];
Manipulate[plot3DWGraph[gcur, Edges[mst], r,
{Glow[Red], Brown}], {r, 0.01, 0.2}],
Initialization : -> (Needs [ "Combinatorica" " ] ;
edgeWeight [ g_, e_] : = GetEdgeWeights [g, {e}];
plot3DWGraph[g_, 1_, r_, col_, op_:l] := Module[ {11} ,
11 = 1≈ Join ≈ (RotateLeft[#, 1] & /@ 1) ;
GraphPlot3D[g,
EdgeRenderingFunction ->
(If[MemberQ[ll, #2] , col,
{Lighter[Hue[edgeWeight[g, #2]], .9],
Opacity[op]}]≈ Join ≈
{Cylinder[#2, Max [ r edgeWeight [ g, #2], 0.01]]} &) ,
VertexRenderingFunction ->
({Yellow, Sphere[#, r+ 0.03]} &) , Boxed -> False] ] ) ]In[75] :=
DynamicModule[{gu, gcur, mst, n = 11},
gu = RandomGraph[n, . 6] ;
While[! ConnectedQfgu], gu = RandomGraph[n, . 6] ] ;
gcur = SetEdgeWeights[gu];
mst = MinimumSpanningTree[gcur] ;
Manipulate[plotWGraph[gcur, Edges[mst], r, Red, Orange],
{r, 0.01, 0.1}],
Initialization : -> (Needs ["Combinatorica" "] ;
edgeW[g_, e_] : = GetEdgeWeights[g, {e}][[l]];
plotWGraph[g_, 1_, r_, coll_, col2_] :=Module[{11},
11 = l ≈ Join ≈ (RotateLeft[#, 1] & /@1) ;
GraphPlot[g, EdgeRenderingFunction ->
(If [MemberQ[ll, #2], {col1, Thickness [r edgeW[g, #2]],
Line[#2]}, {col2, Thickness [r edgeW[g, #2]],
Opacity[0. 4] , Line[#2]}] &),
VertexLabeling -> True] ] ) ]Пример оптимизационной задачи: евклидовы минимальные остовные деревья, триангуляции Делоне, диаграммы Вороного
Если множество вершин графа содержится в метрическом пространстве 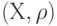 , то весовая функция на ребрах такого графа естественно определяется как
, то весовая функция на ребрах такого графа естественно определяется как 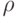 -расстояние между соответствующими вершинами. Минимальное остовное дерево (МОД) в полном графе с вершинами в метрическом пространстве называется метрическим МОД В частном случае, когда метрическое пространство - это евклидово пространство, а весовая функция -евклидово расстояние между точками, метрическое МОД называют ЕМО. В этом примере рассматривается случай евклидовой плоскости. Нам показалось удобнее самим написать процедуру рисования графов. Пунктир изображает полный граф. Отметим, что когда количество точек становится порядка 20 и выше, программа начинает работать все более медленно. Это связано с тем, что алгоритм Краскала имеет порядок сложности, пропорциональный квадрату количества ребер графа, т. е. для полного графа - четвертая степень от количества вершин. (Последнее связа
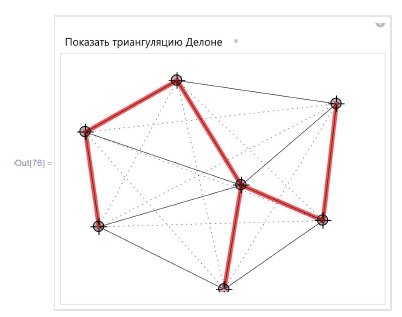
но с тем, что количество ребер полного графа растет квадратично с ростом числа его вершин.) Тут на помощь приходит геометрия. Оказывается, ЕМОД (полного) графа всегда лежит в его специальном подграфе с линейным количеством ребер, а именно, в так называемой триангуляции Делоне:
-расстояние между соответствующими вершинами. Минимальное остовное дерево (МОД) в полном графе с вершинами в метрическом пространстве называется метрическим МОД В частном случае, когда метрическое пространство - это евклидово пространство, а весовая функция -евклидово расстояние между точками, метрическое МОД называют ЕМО. В этом примере рассматривается случай евклидовой плоскости. Нам показалось удобнее самим написать процедуру рисования графов. Пунктир изображает полный граф. Отметим, что когда количество точек становится порядка 20 и выше, программа начинает работать все более медленно. Это связано с тем, что алгоритм Краскала имеет порядок сложности, пропорциональный квадрату количества ребер графа, т. е. для полного графа - четвертая степень от количества вершин. (Последнее связа
но с тем, что количество ребер полного графа растет квадратично с ростом числа его вершин.) Тут на помощь приходит геометрия. Оказывается, ЕМОД (полного) графа всегда лежит в его специальном подграфе с линейным количеством ребер, а именно, в так называемой триангуляции Делоне:
In[76] : =
DynamicModule[{pts, pCG, pts0, w, mst, ее, delauney, showTr},
pts0= {{1, 0}, {0, 1}, {-1, 0}};
Manipulate [vv = Map[{#, VertexNumber -> True} &, pts] ;
pCG = SetEdgeWeights [Graph [CompleteGraph [Length[pts] ] [[!]] , vv] ,
WeightingFunction -> Euclidean] ;
mst = MinimumSpanningTree[pCG]; ее = Edges[mst];
delauney = FromAdjacencyLists [#[[2]] & /@ DelaunayTriangulation [pts] ] ;
Show[If[showTr, {showCG[Length[pts], pts, ее],
showGr[delauney, pts, {Black}]}, showCG[Length[pts], pts, ее]] ,
PlotRange -> {{-2, 2}, {-2, 2}}],
{{pts, pts0}, Locator, LocatorAutoCreate -> True} ,
{{showTr, False, "Показать триангуляцию Делоне"}, {True, False}}],
Initialization: -> (Needs [ "Combinatorica'"] ;
Needs["ComputationalGeometry'"];
showCG [ n_, v_, edg_: { } ] : =
Graphics[GraphicsComplex[v,
If [MemberQ [edg, #11]]], {Red, Thickness [0 . 015] , Opacity [0 . 7] ,
Line[#[[l]]] } , {Blue, Dotted, Line [#[[1]] ] } ] &/@
CompleteGraph [n] [[1]] ] ] ;
showGr[g_, v_, col_: {Blue}] : =
Graphics[GraphicsComplex[v, Append[col, Line[Edges[g] ] ]]];)]Триангуляция Делоне тесно связана с так называемой диаграммой Вороного конечного подмножества M евклидова пространства. Если 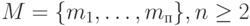 , то ячейкой Вороного точки
, то ячейкой Вороного точки  называется множество
называется множество  для всех
для всех 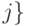 , где через
, где через 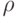 , как и выше, обозначена функция расстояния. Ячейки Вороного точек двухточечного множества
, как и выше, обозначена функция расстояния. Ячейки Вороного точек двухточечного множества 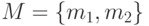 - суть полупространства (в двумерном случае - полуплоскости), порожденные серединным перпендикуляром к отрезку
- суть полупространства (в двумерном случае - полуплоскости), порожденные серединным перпендикуляром к отрезку ![[m_1, m_2]](/sites/default/files/tex_cache/c886163b151d8d0de6b1e7eb808717a9.png) . В общем случае - это выпуклые многогранные области, полученные пересечением соответствующих полупространств:
. В общем случае - это выпуклые многогранные области, полученные пересечением соответствующих полупространств:
In[77] :=
Manipulate[DiagramPlot[ pp] ,
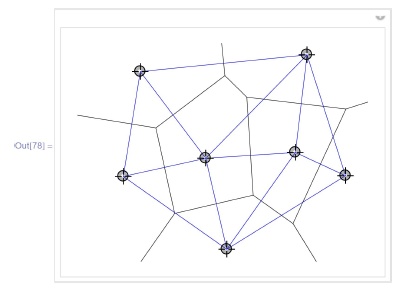
{(pp/ {{0, 0}/ {1- 0}}}, Locator, LocatorAutoCreate -> True}]Триангуляция Делоне - это граф на множестве точек M евклидова пространства, две вершины которого соединены ребром-отрезком, если и только если ячейки Вороного этих вершин пересекаются по множеству коразмерности один. В случае плоскости - по отрезку или лучу.
In[78] : =
DynamicModule[{pts, pts0, vor, delauney},
pts0= {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
Manipulate[
delauney = FromAdjacencyLists [#|[2]] & /@ DelaunayTriangulation[pts] ] ;
Show[{showDiaG[pts], showGr[delauney, pts, {Blue}]},
PlotRange -> {{-2, 2}, {-2,2}}],
{{pts, pts0}, Locator, LocatorAutoCreate -> True}] ,
Initialization: -> (Needs [ "Combinatorica"'" ] ;
Needs["ComputationalGeometry'" ] ;
pairs [ls_] := Table [{Is [i] , Is |[i + 1]] } , {i , 1, Length [Is] - 1} ] ;
showGr[g_, v_f col_: {Blue}] : =
Graphics[GraphicsComplex[v, Append[col, Line [Edges [gr] ] ] ] ] ;
showDiaGfpp ] := Module [ {hh, vd, In, edg, rs, els},
vd = VoronoiDiagram [pp] ; hh = Head[#] & /@ vd[[l]| ;
In =
Union[
Sort /@ Flatten [pairs [#] & /@
Select [ Table [ Select [vd [[2, i, 2] , hh[[#]| == List &] ,
{i, 1, Length [vd [[2]] }] , Length[#] > 1 &] , 1] ] ;
edg = Line[vd[[1]][[#]] ] &/@ In; rs = Select [vd[[l]] , Head[#] == Ray &] ;
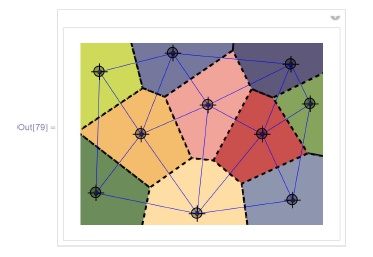
Graphics [edg ≈ Join ≈ (Line /@ Apply [List, rs , {1}])]];)]На следующей картинке ячейки Вороного раскрашены в разные цвета:
In[79] :=
DynamicModule [ {pts, pts0, vor, delauney},
pts0 = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
Manipulate[
delauney = FromAdjacencyLists[#[[2]] & /@ DelaunayTriangulation[pts]] ;
Show[{showDia[pts], showGr[delauney, pts, {Blue}]},
PlotRange -> {{-2, 2} , {-2, 2}}] , {{pts, pts0}, Locator, LocatorAutoCreate -> True}] ,
Initialization: -> (Needs [ "Combinatorica" " ] ;
Needs["ComputationalGeometry'"];
showGr[g_ , v_ , col_ : {Blue}] : =
Graphics[GraphicsComplex[v, Append[col, Line [Edges [g]] ] ] ] ;
append[l_, r_] := Module [ {bg, en, res},
If [Length[r] ≠ 4, res = 1 ≈ Join ≈ r,
bg = r[[{l, 2}];
en = r[[{3, 4}];
Which[
bg[[1]] == 1[l] , res = {bgI2]; bgPI } ≈ Join ≈ 1,
bg[[2]] == 1[[l] , res = bg ≈ Join ≈ 1,
bg[[1]] == 1[[-l]], res = l ≈ Join ≈ bg,
bg[[2]] == 1[[-1]], res = 1 ≈ Join ≈{bg[[2]] , bg[[1]]}
];
Which[
en[[1]] ==1[[1]], res = {enI2I , en III }≈ Join ≈res ,
en[[2]] == 1[[1]], res = en ≈ Join ≈ res,
en[[1]] ==1[[-1]], res = res ≈ Join ≈ en,
en[[2]] ==1[[-1]], res = res ≈ Join ≈ {en[[2]], en[[1]]]}]
];
res
];
showDia[pp_] : = Module[{hh, vd. In, rs, els, pi},
vd = VoronoiDiagram[pp] ; hh = Head[#] & /@vdlll ;
ln = vdIlH#I & /@ Table [Select [vd[2, i, 2]| , hhl#] == List S] ,
{i, 1, Length[vdI2J]}];
rs = Map[If [Length[#] > 0, Flatten [Apply [List, it, 1] , 1] , {}] &,
vd[[1]][[#]] & /@ Table [Select [vd [[2, i, 2]], hh[[#]] == Ray &] ,
{i, 1, Length[vd[[2]] ]}]] ;
cls = MapThread[append[#1, #2] &, {In, rs}] ; pi = Polygon[#] & /@ cls;
Graphics[Table[{EdgeForm[{Thick, Dashed}],
ColorData[Length[pp], "ColorList"][[i]], Opacity[0.7],
pl[[i]], Black, PointSize[0.02] , Point[pp[[i]] ] } ,
{i, 1, Length [pp]}]]];
)
]Возвращаясь к задаче о ЕМОД, с помощью триангуляции Делоне можно построить квадратичный (по количеству вершин) алгоритм построения ЕМОД. А именно, сначала строим триангуляцию Делоне, а затем уже к ней применяем алгоритм Краскала:
In [80] : =
DynamicModule[{pts, ptsO, mst, ее, delauney, showTr},
pts0= {{1, 0}, {0, 1}, {-1, 0}};
showGr[g_, v_, col_: {Blue}] : =
Graphics [GraphicsComplex[v, Append [ col, Line [Edges [g-] ] ]]];
Manipulate[
delauney = SetEdgeWeights[
FromAdjacencyLists [#[[2]] & /@ DelaunayTriangulation [pts] , pts] ,
WeightingFunction -> Euclidean] ;
mst = MinimumSpanningTree[delauney] ;
Show[
If[showTr, {showGr[mst, pts, {Red, Thickness[0.01], Opacity[0.7]}],
showGr[delauney, pts, {Blue}]},
showGr[mst, pts, {Red, Thickness[0.01]}]],
PlotRange ->
{{-2, 2}, {-2, 2}}], {{pts, pts0}, Locator, LocatorAutoCreate -> True} ,
{{showTr, False, "Показать триангуляцию Делоне"}, {True, False}}],
Initialization : -> (Needs [ "Combinatorica' " ] ;
Needs["ComputationalGeometry *"])
]Замечание 7.3.1. На самом деле в общем случае алгоритм Краскала построения МОД работает со скоростью  , а алгоритм построения ЕМОД, использующий триангуляцию Делоне, - со скоростью
, а алгоритм построения ЕМОД, использующий триангуляцию Делоне, - со скоростью 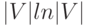 .
.
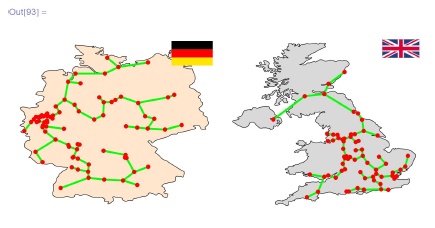
В качестве примера построим минимальные остовные деревья, соединяющие крупные города Германии и Великобритании. Напомним, Mathematica включает в себя большие базы данных по естественным наукам, в частности, по географии. Эти базы данных, впрочем, находятся на сайте компании Wolfram, поэтому, чтобы ими пользоваться непосредственно, нужен доступ к сети. В приведенных примерах мы просто выкачали информацию о геометрической форме страны и ее флаге из базы CountryData, и координаты и названия крупных (больше 100000 жителей) городов выбранных стран из базы CityData. Отметим также наличие баз данных по молекулярной биологии, астрономии, физике, химии, лингвистике, финансам и пр. (см. Scientific & Technical Data ).
In[81] : =
germCitiesCoord = {{{52.52 ", 13.38 "}}, {{53.55 ", 10. '}}{* ... *) } ;
ukCitiesCoord = {{{51.5", -0.1166667"}}, {{52.4666667", -1.9166667"}}
(* . . . *)};
germCitiesNames = {"Berlin", "Hamburg", "Munich", "Cologne" (* ... *)};
ukCitiesNames = {"London", "Birmingham", "Glasgow", "Liverpool" (* ... *)};
germPoly =
Polygon[{{{5.90725', 50.7242'}, {6.02985', 50.8203'}, {6.07395', 50.8833'},
{6.08445', 50.9323}, {6.05505', 50.9715}, {6.02985', 50.9785}
(* ... *)}, {{13.9187', 53.886'}, {13.8735', 53.8918},
{13.87', 53.9166'} (. ... *)} (* ... *)}];
ukPolygon =
Polygon[{{{-5.80035', 55.3191'}, {-5.83335', 55.3252'},
{-5.8559', 55.3505'}},
{{-7.1481', 55.1193-}, {-7.1613', 55.0969'}, {-7.154', 55.0852}
(* ... *)} (* ... * }];sph[v_] := {Cos [v[[ll] Degree] Cos [v|[2]] Degree] ,
Cos [v[[ll] Degree] Sin [v[[2I] Degree] , Sin[v[[ll] Degree] } ;
geoDist[a_, b_] := N[2 ArcSin [Norm [sph [afl2]] ] - sph[b[[2]j] ] /2] ] ;
Needs["Combinatoricav"];
geoMST [ cnt_] : =
Module[{cts, ctsT, names, flag, poly, edges, gWeight, mst, col},
If[cnt == "Germany", cts = germCitiesCoord; names = germCitiesNames;
flag = gflag; col = LightOrange; poly = germPoly, cts = ukCitiesCoord;
names = ukCitiesNames; flag = ukflag; poly = ukPolygon; col = LightGray];
edges = Edges[CompleteGraph[Length[cts]] , All] ;
gWeight = SetEdgeWeights[Graph[edges, cts] , WeightingFunction -> geoDist] ;
mst = Edges[MinimumSpanningTree[gWeight]] ;
ctsT = Reverse /@ Flatten [cts, 1] ;
Graphics[{col, EdgeForm[Black], poly, Thick, Green,
MapThread[Line[{#2, &2}] &, {ctsT[I^[[l]]I &/@mst, ctsT[I#[[2I]I &/@ mst}],
PointSize [Medium] , Red,
MapThread [Tooltip [Point [#1] , #2] &, {ctsT, names}] ,
Inset[flag, {Right, Top}, {Right, Top}, 2]}]
];
GraphicsRow [geoMST [#] & /@ { "Germany" , "UnitedKingdom" } ]