НОУ ИНТУИТ | Практикум по компьютерной геометрии. Лекция 7: Графы в компьютерной геометрии

Опубликован: 27.12.2010 | Доступ: свободный | Студентов: 1030 / 278 | Оценка: 5.00 / 5.00 | Длительность: 18:38:00

ISBN: 978-5-9556-0117-5

Темы: Математика, САПР

Специальности: Математик

Теги: алгебра, анализ, вычисления, геометрия, программное обеспечение

Вам нравится? Нравится 14 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

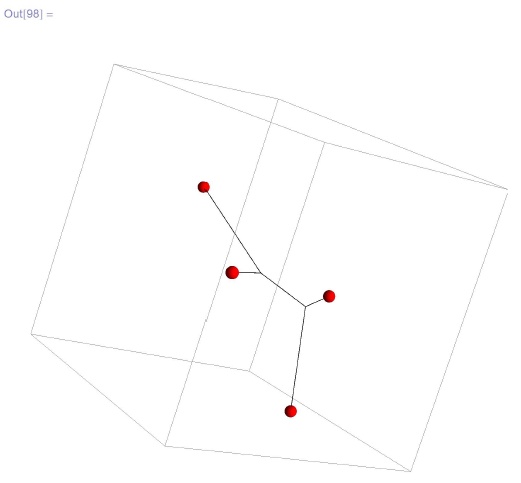
Замечание об управлении. При наведении курсора на граничную (красную) вершину сети (см. ниже), вершина становится желтой. Чтобы выделить граничную вершину сети, позиционируйте курсор на этой вершине и нажмите Ctrl. Вершина станет зеленой, "прикрепится" к курсору мыши и будет следовать за ним. Чтобы отпустить вершину, нажмите Shift. Вершина вновь станет красной. Нажимая левую клавишу мыши при курсоре, позиционированном на картинке, и двигая курсор, вы будете вращать картинку. Обратите внимание на скачкообразные перестройки структуры сети (бифуркации):

In [98]:=
    DynamicModule[{pp, Locator3D, MyMean, testPoint, st, net4}, 
        Locator3D[pts0_, ?_: Line] : = 
           DynamicModule [{pts, ppp, cur, с = False, covered = False, g, msAlt, bds, bm=-l, 
              bM = 1, ptsAlt, i - 1, testln = 2} , 
             pts = pts0; ptsAlt = {0, 0, 0} ; msAlt ={{1.3, -2.4, 2.}, {-1.3, 2.4, -2.}}; 
             cur = Dynamic[MousePosition["Graphics3DBoxIntercepts", msAlt]]; 
             g=Graphics3D[Map[{Red, Sphere[#, 0.05]} &, 
                    If [c, Drop[pts, {3}], pts] ] ≈ Join ≈
                  Table[ 
                    If [CurrentValue ["ControlKey"] bbcovered, с = True; msAlt = #; ptsAlt = pts[[j]] ; 
                    If[CurrentValue["ShiftKey"], с = False];
                    testln = Length[CurrentValue[{"MousePosition", "GraphicsImageScaled"} ] ] ; 
                    If [c, If [testln < 2, ptslij = ptsAlt] ; 
                        bds = Transpose [AbsoluteOptions [g, PlotRange] [[1, 2]] ]; 
                        bm = 0 . 7 bds [[1]] ; 
                        bM = 0 . 7 bds [[2]] ; 
                        ppp = MyMean [pts [[j]] , #] ;
                        pts[[j]] = MapThread[Max[Min[#I, #3] , #2] &, {ppp, bm, bМ}]; 
                        ptsAlt = pts[[j]]; 
                        msAlt = #] ; 
                    If [c, If [i == j, {Green, Sphere[pts[[i]] , 0.07]}, {}], 
                     If [ (testln >= 2) && (testPoint[pts[[i]] , #] < 0.01 ) , covered = True; j = i; 
                        {Yellow, Sphere[pts[[i]], 0.07]}, covered=False; {}]], 
                    {i , 1, Length [pts] } ] ≈ Join ≈ {f[pts] } & /@ cur, 
               Boxed -> True, PlotRange -> ({-1.3, 1.3}, {-1.3, 1.3}, {-1.3, 1.3}}],
           Initialization : -> (

$\begin{matrix} &&&MyMean[p_{-} , ms_{-} ] :=ms[[1]]+(ms[[2]]-ms[[1]]) \frac{(ms[[2]]-ms[[1]]).(p-ms[[1]])}{(ms[[2]]-ms[[1]]).(ms[[2]]-ms[[1]])}; \end{matrix}\\ \begin{matrix} &&&testPoint[p_{-}, ms_{-}] : = \end{matrix}\\ \begin{matrix} &&&Module[\{v\}, v = p - ms[[1]]-(ms[[2]]-ms[[1]])\frac{(ms[[2]]-ms[[1]]).(p-ms[[1]])}{(ms[[2]]-ms[[1]]).(ms[[2]]-ms[[1]])};v.v]; \end{matrix}$

)];
   st[gr_, ls_] : = 
      Quiet@Module [{vv, ее, len} , vv = First @g; ее = Last@g;
            len = Plus @@ (EuclideanDistance @@ vv[[#]] &/@ee);
            FindMinimum [ len, {#, RandomReal [ ] } &/@ Flatten [w[[ls]] ] , Method -> "PrincipalAxis"]≈ 
                Join ≈ {g-}] ;
      net4[p_] := Module [ {gl, g2 , g3, gg, res, min, resl, gr, sub, v, e, xl, yl, zl, x2 , y2 , z2}, 
          gl = {(# &, /@p) ≈ Join ≈ {{xl, yl, zl}, {x2, y2, z2}} ,
              {{1, 5}, {2, 5}, {5, 6}, (6, 3}, {6, 4}}}; 
          g2 = { (# & /@p) ≈ Join ≈ {{xl, yl, zl}, {x2, y2, z2}},
               {{1, 5}, {3, 5}, {5, 6}, {6, 2}, {6, 4}}}; 
          g3 = { (# & /@ p) ≈ Join ≈ {{xl, yl, zl}, {x2, y2, z2}},
               {{1, 5}, {4, 5}, (5, 6), {6, 3}, (6, 2}}}; 
          gg = {gl, g2, g3} ; res = st[#, {5, 6}] & /@gg; min = Min[#[[l]] & /@ res] ; 
          resl = Select[res, #[[1]] == min &] // First; gr = resl // Last; sub = resl[[2]] ; 
          v = First@gr /. sub; 
          e = Last@gr; 
          Line[v[[#]] ] &, /@ e] ; 
      рр={{-1, 0, -1}, {-1, 0, 0}, {-1, 1, 0}, {1/2, 1/2, 1/2}}; 
      рр={{-1, 0, -1), {-1, 0, 0}, {-1, 1, 0}, {1/2, 1/2, 1/2}}; 
      Locator3D[pp, net4]]

Из сказанного выше следует, что каждая кратчайшая сеть является деревом с терминалами степени не выше 3 и дополнительными вершинами степени 3. Отсюда вытекает, что если n - число терминалов, то дополнительных вершин может быть не больше n - 2 (проверьте). Тем самым имеется конечное, хотя и экспоненциально растущее с ростом n, число комбинаторных структур кратчайших сетей. Доказано, что проблема Штейнера на евклидовой плоскости является NP -трудной, т. е. скорее всего не существует полиномиального по n алгоритма построения кратчайшей сети.

Тем не менее в последнее время разработаны достаточно быстрые алгоритмы, позволяющие строить кратчайшие сети для сотен точек. Приведем визуализацию одного свойства решения задачи Ферма, лежащего в основе всех точных алгоритмов.

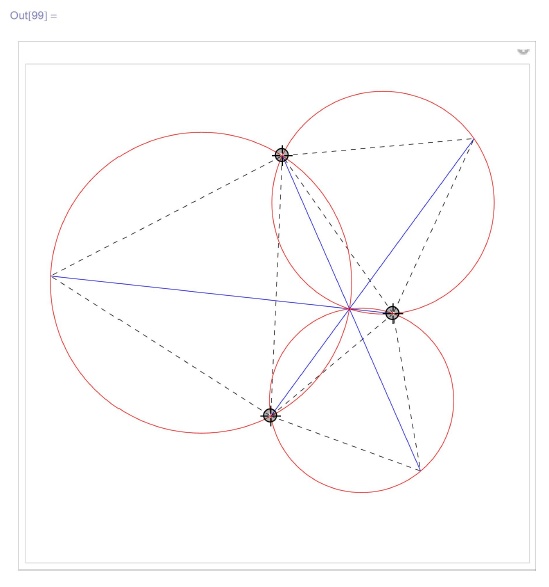
Если на сторонах треугольника построить правильные треугольники, пересекающие исходный только по его сторонам, то три окружности (изображенные красным цветом), описанные вокруг построенных треугольников, пересекутся в одной точке. В той же точке пересекутся и три отрезка (изображенные синим цветом), каждый из которых соединяет добавленную вершину построенного правильного треугольника с противоположной ей вершиной исходного.

Если в треугольнике, построенном на терминалах, все углы не превосходят 120^0 , то общая точка пересечения красных окружностей и синих отрезков совпадает с решением задачи Ферма. Если же некоторый угол больше или равен 120^0 , то решение задачи Ферма - вершина этого угла:

In [99]:=
         Manipulate[
            Module [ {pc, рр, i , sign, pt3 = { } , tri = { } , seg = { } , 
                с, r, circ = { } , dist, vec} ,

$\begin{matrix} &&&dist[v_{-}, w_{-}] : = \sqrt{(v - w) . (v - w)} ; \end{matrix}$

vec[v_] := {Re[v],Im[v]}; 
               pp = p ;
               For i = 1, i <= 3, i++,
                 pc = Complex @@ # & /@ pp ;
                 sign = Sign[Det[{pp [[3]] -pp[[1]], pp[[2]] -PP[[1]] } ] ] ;
                 If[sign ≠ 0,
                    pt3=pc[[1]]e^{-sing i π/3} + pc[[2]] e^{sing I π/3};
                    с = Mean [{pp [[1]], pp[[2]], vec@pt3}];
                    r = dist[c, pp[[1]]] ;
                    tri = tri ≈ Join ≈ {{pp[[1]] , pp[[2]] , vec@pt3, pp[[1]]}};
                    seg = seg ≈ Join ≈ { {vec@pt3, рр[[3]] } } ;
                    circ = circ ≈ Join ≈{ {с, r}};
      ];
      pp = RotateLeft[pp];
       ] ,
    Graphics [ { {Dashed} ≈ Join ≈ (Line /@ tri) } ≈ Join ≈ {Blue} ≈ 
        Join ≈ (Line /@ seg) ≈ Join ≈ {Red} ≈ Join ≈ 
          (Circle @@ # & /@ circ) , PlotRange -> {{-2, 2}, {-2, 2}}, 
        AspectRatio -> Automatic]
       ] ,
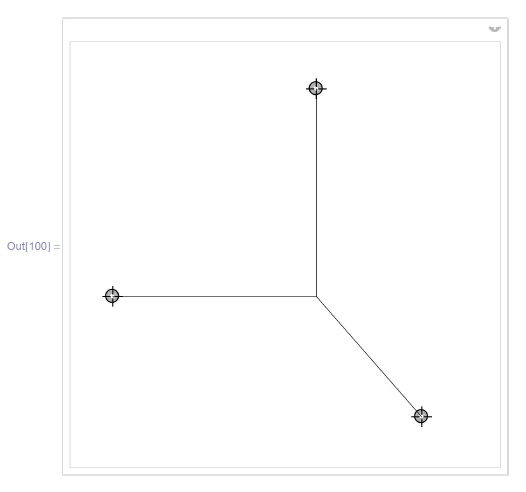
    {{p, {{-1, 0}, {1, 0}, {0, 1}}}, Locator}]

Если заменить евклидово расстояние на манхеттенское, т. е. порожденное нормой 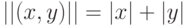||(x,y)||=|x|+|y| , то соответствующие кратчайшие сети используются при проектировании микросхем.

Поэкспериментируйте с примером, приведенным ниже, и постарайтесь сформулировать правило, описывающее направление отрезков.

In[100] :=
        Manipulate[Module[{x, y, s, distManhat}, 
           distManhat[v_, w_] : = Plus @@ Abs@ (v - w) ; 
           s = 
             {x, y} /. 
                Last@ 
                  Quiet @ FindMinimum [Plus @@ (distManhat [ {x, y} , #] &/@p) , 
                     {{x, First@Mean[p]} , {y, Last@Mean[p]}} , 
                     Method -> "PrincipalAxis"]; 
                Graphics [Line [{s, #}] &/@p, PlotRange -> { {-2 , 2}, {-2, 2}}, 
                    AspectRatio -> Automatic] ] , 
            {{p, {{-1, 0}, {1, 0}, {0, 1}}}, Locator}
       ]

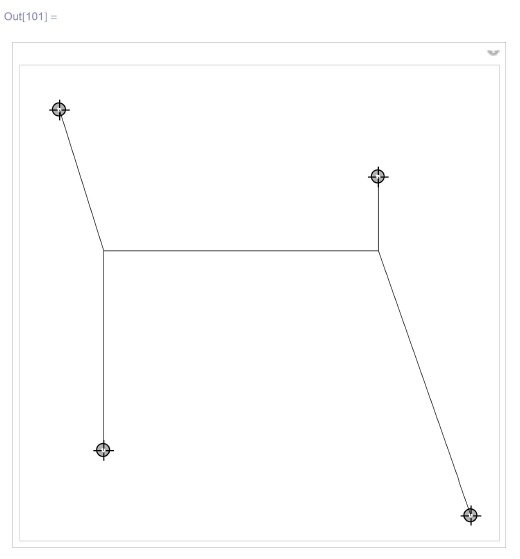
Ниже приведена реализация кратчайшей сети на манхеттенской плоскости в случае четырех терминалов. Обратите внимание на скачкообразное изменение кратчайшей сети при смещении терминалов. Эта особенность поведения сети объясняется неоднозначностью решения, в отличие от евклидова случая.

In [101] :=
         Manipulate[ 
            Module [{gl, g2 , g3, xl, yl, x2, y2 , min, res, resl, gr, 
                sub, v, e, distManhat, st, MyShowGraph} , 
              distManhat[v_, w_] : = Plus @@ Abs@ (v - w) ; 
              st[g_, ls_] : = 
                 Quiet@Module [ {w, ее, len} , w=Vertices[g];
                     ее = Edges [g] ; len = Plus @@ (distManhat @@vv[[#]] & /@ee) ; 
                    FindMinimum [len, {#, RandomReal [ ] } &/@ Flatten [w[[ls]] ] , 
                       Method -> "Newton"] ≈ Join ≈ {g}] ; 
              MyShowGraph[g_, opts : OptionsPattern[Graphics]] : = 
                 Module [ {vv, ее} , vv = Vertices [g] ; ее = Edges [g] ; 
                   Graphics [Line [vv[[#]] ] & /@ ее, opts] ] ; 
              gl = Graph[{{{l, 5}}, {{2, 5}}, {{5, 6}}, {{6, 3}},
                       {{6, 4}}}, ({#} &/@p) ≈ Join ≈ {{{xl, yl}}, {{x2, y2}}}]; 
             g2 = Graph[{{{l, 5}}, {{3, 5}}, {{5, 6}}, {{6, 2}},
                       {{6, 4}}}, ({#} &/@p) ≈ Join ≈ {{{xl, yl}}, {{x2, y2}}}]; 
            g3 = Graph[{{{l, 5}}, {{4, 5}}, {{5, 6}}, {{6, 3}},
                       {{6, 2}}}, ({#} &/@p) ≈ Join ≈ {{{xl, yl}}, {{x2, y2}}}]; 
            g= {gl, g2, g3}; res = st[#, {5, 6}] &/@g; min = Min[#|[l]] & /@res] ;
            resl = Select [res, #[[1]] == min &] // First; 
            gr = resl // Last; 
            sub = resl [[2]] ; 
            v = Vertices[gr] /. sub; 
            e = Edges [gr] ;
           MyShowGraph[AddEdges[AddVertices[EmptyGraph[0], v] , e] , 
              PlotRange -> {{-2, 2}, {-2, 2}}]
          ],
         {{p, {{-1, 1}, {-1, -1}, {1, -1}, {1, 1}}}, Locator}, 
         Initialization : -> (
Needs["Combinatorica""]; 
    )]

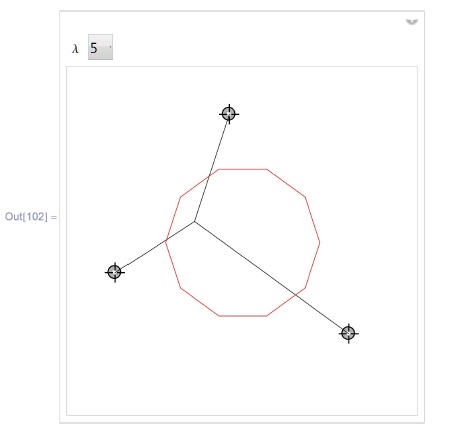
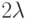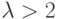Отметим, что единичная окружность на манхеттенской плоскости является квадратом, диагонали которого лежат на координатных осях. Обобщением манхеттенской метрики являются так называемые $\lambda$ -нормы, для которых единичная окружность - правильный $2 \lambda$ -угольник. Ниже приводится визуализация кратчайших сетей на $\lambda$ -нормированной плоскости в случае трех терминалов. При $\lambda > 2$ вновь отмечается скачкообразное поведение сетей при cмещении терминальных точек, что опять же объясняется неоднозначностью решения.

In[102] :=
     Manipulate [
          Module {x, y, s, lin, vec, nrf norm, cr, len, res, gsol, distNorm} , 
              vec[v_] :={Re[v], Im[v]};
           nr = vec@# & /@ Table [е^{I π/2(k+1/2)} , {к, 0, λ - 1);
           norm [v_] :=(Max@@(Abc[@.v]&/@nr)/(nr[[1]].{1,0});
              distNorm [v_, w_] : = norm [v - w] ;
              cr = ParametricPlot[({Cos[ϕ],Sin[ϕ]})/(norm[{Cos[ϕ], Sin[ϕ]}]),{ϕ,0,2π},}
              PlotStyle -> {Red}];
              len = Plus @@ (distNorm[{x, y} , #] & /@ p) ;
              res = Quiet@FindMinimum[len, {{x, RandomReal [ ] } , {y, RandomReal [ ] }} ,
                       Method -> "Newton"]; 
                   s = {x, y} /. Last@res; 
                  Show[{Graphics[Line[{s, #} ] & /@ p, PlotRange -> { {-2 , 2} , {-2,2}},
                        AspectRatio -> Automatic] , cr}] 
                    ] , {{λ, 3}, Rest@Range[20] }, {{p, {{-1, 0}, {1, 0}, {0, 1}}}, Locator}]

Дальше >>

Авторизоваться

Практикум по компьютерной геометрии

Графы в компьютерной геометрии

Вопросы и ответы