НОУ ИНТУИТ | Практикум по компьютерной геометрии. Лекция 8: Тензоры: опыт создания пользовательского пакета программ

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 27.12.2010 | Доступ: свободный | Студентов: 1030 / 278 | Оценка: 5.00 / 5.00 | Длительность: 18:38:00

ISBN: 978-5-9556-0117-5

Темы: Математика, САПР

Специальности: Математик

Теги: алгебра, анализ, вычисления, геометрия, программное обеспечение

|

Вам нравится? Нравится 14 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Данная лекция преследует две цели: показать, как в Mathematica можно работать с такими достаточно сложными математическими объектами, как тензоры, и продемонстрировать на примере тензорного исчисления, как можно расширить стандартные возможности Mathematica с помощью написания своих собственных программ.

Ключевые слова: связь, таблица, вектор, Произведение, calculus, матрица Якоби, аргумент, имя файла, файл, значение, матрица перехода, assumption, базис системы, skewing

Встроенные возможности Mathematica для работы с тензорами

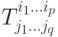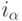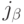Напомним, что тензором T типа (p,q) на n -мерном векторном пространстве V называется соответствие, приписывающее каждому базису $е_1, \dots, е_n$ набор чисел $T_{j_1 \dots j_q}^{i_1 \dots i_p}$ , где каждый из p + q штук индексов $i_{\alpha}$ и $j_{\beta}$ независимо пробегает значения от 1 до n. При этом требуется, чтобы наборы, приписанные разным базисам, были связаны друг с другом специальным образом. Эта связь называется тензорным законом и полностью определяется количествами верхних и нижних индексов. Число p + q называется рангом тензора.

Из сказанного выше вытекает, что при фиксированном базисе тензор -это многомерная таблица, состоящая из 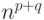$n^{p+q}$ чисел. Скаляр, т. е. тензор типа (0,0), представляет собой нульмерную таблицу, вектор или ковектор, являющиеся соответственно тензорами типа (1,0) и (0,1) - одномерные, скалярное произведение (тензор типа (0,2)) или линейный оператор (типа (1,1)) - двумерные.

В пакете Mathematica реализованы многообразные способы задания и работы с такими, и даже существенно более общими, таблицами. Мы уже неоднократно пользовались ими, работая с теми или иными списками List. Выясним, чем выделяются списки, соответствующие тензорам, из общих списков List, а также какие имеются встроенные возможности для моделирования тензоров. Отметим сразу, что непосредственное использование встроенных функций не приводит к желаемому результату, поэтому разрабатываются специальные дополнительные библиотеки, которые подключаются к Mathematica командой Get[] или Needs[]. Вот некоторые примеры таких пакетов:

пакет Ricci, разработанный John M. Lee и Co (http://www.math.washington.edu/lee/Ricci/);
TensorManipulation, J.R. Ruiz-Tolosa and E. Castillo (http://personales.unican.es/castie/tensors/);
Riemannian Geometry & Tensor Calculus @ Mathematica, Sotirios Bonanos (http://www.inp.demokritos.gr/sbonano/RGTC/RiemannTensorCalculus.html);
Tools of Tensor Calculus A. Balfagon, P. Castellvi and X.Jaen (http://baldufa.upc.edu/xjaen/ttc/index.htm).

Приведенные пакеты бесплатны. Имеются также платные, например, Cartan и MathTensors, H. Soleng (http://library.wolfram.com/infocenter/Articles/2280/).

Мы проиллюстрируем, как научить Mathematica работе с тензорами на примере нашей собственной разработки.

Списки, соответствующие тензорам

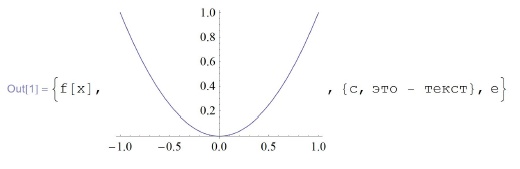
Напомним, что список List в Mathematica представляет собой записанную в фигурных скобках последовательность любых объектов, например:

In[1]:= {f [х] , Plot[x², {х, -1, 1}], {с, "это - текст"}, е}

Тензоры, с которыми мы будем здесь работать, отличаются от общих списков, во-первых, тем, что конечные элементы списка - числа или переменные. Во-вторых, тензорам соответствуют однородные списки. Последнее означает, что каждый из подсписков состоит из одного и того же числа элементов, являющихся или числами (переменными), или подсписками одной и той же структуры.

Ниже приведены примеры двух списков, первый из которых - тензор, а второй - нет:

In[2]:={{1, 2}, {3, 4}}
       {{1, 2}, {3, 4, 5}}
Out[2]={{l, 2}, {3, 4}}
Out[3]={{l, 2}, {3, 4, 5}}

Чтобы по списку T, представляющему тензор ранга больше нуля, понять размерность соответствующего линейного пространства V, достаточно выполнить команду Length[T] , например:

In[4] := Length [{{1, 2}, {3, 4}} ]
Out[4] = 2

Можно также выполнить команду Dimensions и взять произвольный элемент, например первый:

In[5] : = Dimensions [{{1, 2}, {3, 4}} ]
               First@Dimensions[{{l, 2}, {3, 4}} ] 
                  (* напомним, что 
                      f@x - инфиксная форма команды f[x]*)
Out[5] = {2, 2 }
Out[6] = 2

Отметим, что Dimensions применима к спискам или выражениям, у которых на каждом уровне находятся списки или выражения одной и той же структуры, однако длины подсписков могут быть уже разными (поэтому команда Dimensions выдает длины подсписков всех уровней):

In[7]: = Dimensions[{{l, 2, 3}, {4, 4, 6}} ]
Out[7] = {2, 3 }

Чтобы по списку T, представляющему тензор ранга больше нуля, понять, чему равен его ранг, выполните команду ArrayDepth[T] , например:

In[8]: = ArrayDepth[{{l, 2}, {3, 4}} ]
Out[8] = 2

Тензор ранга 0, значение которого - число или простая переменная, также правильно обрабатывается:

In[9] :=ArrayDepth[3] 
        ArrayDepth[x]
Out[9] = 0
Out[10] = 0

Однако эта команда применима и к выражениям, для которых выдает ранг структуры, индексирующей все части выражения, что может приводить к нежелательному результату:

In[11] : = ArrayDepth[xi]
Out[11] = l

хотя

In[12] : = ArrayDepth [ {х₁ } ]
Out[12] = l

Замечание 8.2.1. Не путайте ArrayDepth с Depth, который выдает число индексов, необходимых для описания всех частей выражения, плюс 1. Например:

In[13]:= ArrayDepth[{{1, 2}, (x₁, 4}} ] 
         Depth[{{1, 2}, {х₁; 4}} ]
Out[13] = 2
Out[14] = 4

В последнем случае результат 4 получатся, во-первых, за счет прибавления упомянутой выше 1, а во-вторых, из-за того, что на описание частей обозначения x_1 требуется два индекса (чтобы добраться до нижнего индекса 1).

Тензоры сложной структуры можно наглядно представить с помощью команды MatrixForm:

In[15] :=DynamicModule [ {vars, k, r} , 
             Manipulate[vars = Table[
                 Symbol["i" <>ToString[k]], {k, r}]; 
               MatrixForm@Table [Plus @@ vars,
                   Evaluate [ Sequence @@ ({#, 3} &/@vars)]], 
            {r, Range[5]}]]

Создание таблиц

К стандартным средствам создания таблиц относятся команды Table, Array, ConstantArray и SparseArray. С первыми двумя командами мы познакомились еще в прошлом семестре.

In[16]:= Table[{i, j, k} , {i, 3}, {j, 3} , {k, 3}] 
         Array[{#2, #2, #3} &, {3, 3, 3} ]
Out[16]={{{{l, 1,1}, {1, 1, 2}, {1, 1, 3}},
          {{1, 2,1}, {1, 2, 2}, (1, 2, 3}},
          {{1, 3,1}, {1, 3, 2}, {1, 3, 3}}},
        {{{2, 1,1}, {2, 1, 2}, {2, 1, 3}}, {{2, 2, 1}, {2, 2, 2},
          {2, 2,3}}, {{2, 3, 1}, {2, 3, 2}, {2, 3, 3}}},
        {{{3, 1,1}, {3, 1, 2}, {3, 1, 3}}, {{3, 2, 1}, {3, 2, 2},
          {3, 2,3}}, {{3, 3, 1}, {3, 3, 2), {3, 3, 3}}}}
Out[17]={{{{l, 1,1}, {1, 1, 2}, {1, 1, 3}},
          {{1, 2,1}, {1, 2, 2}, (1, 2, 3}},
          {{1, 3,1}, {1, 3, 2), {1, 3, 3}}},
         {{{2, 1,1}, {2, 1, 2}, {2, 1, 3}}, {{2, 2, 1}, {2, 2, 2},
           {2, 2,3}}, {{2, 3, 1}, {2, 3, 2}, {2, 3, 3}}},
         {{{3, 1,1}, {3, 1, 2}, {3, 1, 3}}, {{3, 2, 1}, {3, 2, 2},
           {3, 2,3}}, {{3, 3, 1}, {3, 3, 2}, {3, 3, 3}}}}

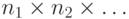Команда ConstantArray[c,n] создает список из n копий элемента c, а $ConstantArray[c, \{n_1,n_2, \dots \}]$ создает $n_1 \times n_2 \times \dots$ список вложенных списков, содержащих копии элемента c:

In[18] := Cons tantArray [5, 10]
          ConstantArray[5, {3, 3, 3}]
0ut[18] = {5, 5, 5, 5, 5, 5, 5, 5, 5, 5}
Out[19] = {{{5, 5, 5}, {5, 5, 5}, {5, 5, 5}}, 
           {{5, 5, 5}, {5, 5, 5}, {5, 5, 5}}, 
           {{5, 5, 5}, {5, 5, 5}, {5, 5, 5}}}

Команда SparseArray предназначена для создания списков, в которых лишь некоторые элементы отличаются от данного элемента с, являющегося по умолчанию нулем. При этом отличные от с элементы val_i задаются по формату $роs_i \to val_i$ где роs_i - положение этого элемента. При этом, если не указывать специально, размеры полученной таблицы выбираются наименьшими возможными. В приведенном ниже примере строится таблица 3x4x3:

In[20]:=SparseArray[{{2, 3, 2} -> 1, {3, 4, 3} -> 9}]
        SparseArray[{{2, 4, 2}->1, {3, 4, 3}->9}] // MatrixForm
Out[20] = SparseArray [<2>, {3, 4, 3}]

$Out[21]=\begin{pmatrix} \begin{pmatrix}0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\0\end{pmatrix}\\ \begin{pmatrix}0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\1\\0\end{pmatrix}\\ \begin{pmatrix}0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\9\end{pmatrix} \end{pmatrix}$

Если нужно построить таблицу заданных размеров, эти размеры можно указать списком в следующем аргументе:

In[22] := SparseArray [{{2, 3, 2} -> 1, {3, 4, 3}->9}, {4, 4, 4}] 
           SparseArray[{{2, 4, 2} ->1, {3, 4, 3} -> 9} , {4, 4, 4}] // 
            MatrixForm
Out[22] = SparseArray [<2>, {4, 4, 4}]

$Out[21]=\begin{pmatrix} \begin{pmatrix}0\\0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\0\\0\end{pmatrix}\\ \begin{pmatrix}0\\0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\1\\0\\0\end{pmatrix}&\begin{pmatrix}0\\1\\0\\0\end{pmatrix}\\ \begin{pmatrix}0\\0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\9\\0\end{pmatrix}\\ \begin{pmatrix}0\\0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\0\\0\end{pmatrix}&\begin{pmatrix}0\\0\\0\\0\end{pmatrix} \end{pmatrix}$

Наконец, после списка размерностей можно указать элемент, который будет располагаться на не заданных явно позициях списка:

In[24]:=SparseArray[{{2, 3, 2} -> 1,
         {3, 4, 3} -> 9}, {4, 4, 4}, х]
        SparseArray[{{2, 4, 2} -> 1,
         {3, 4, 3} -> 9}, {4, 4, 4}, х] // MatrixForm
Out[24] = SparseArray [<2>, {4, 4, 4}, х]

$Out[21]=\begin{pmatrix} \begin{pmatrix}x\\x\\x\\x\end{pmatrix}&\begin{pmatrix}x\\x\\x\\x\end{pmatrix}&\begin{pmatrix}x\\x\\x\\x\end{pmatrix}&\begin{pmatrix}x\\x\\x\\x\end{pmatrix}\\ \begin{pmatrix}x\\x\\x\\x\end{pmatrix}&\begin{pmatrix}x\\x\\x\\x\end{pmatrix}&\begin{pmatrix}x\\1\\x\\x\end{pmatrix}&\begin{pmatrix}x\\1\\x\\x\end{pmatrix}\\ \begin{pmatrix}x\\x\\x\\x\end{pmatrix}&\begin{pmatrix}x\\x\\x\\x\end{pmatrix}&\begin{pmatrix}x\\x\\x\\x\end{pmatrix}&\begin{pmatrix}x\\x\\9\\x\end{pmatrix}\\ \begin{pmatrix}x\\x\\x\\x\end{pmatrix}&\begin{pmatrix}x\\x\\x\\x\end{pmatrix}&\begin{pmatrix}x\\x\\x\\x\end{pmatrix}&\begin{pmatrix}x\\x\\x\\x\end{pmatrix} \end{pmatrix}$

Дальше >>

Авторизоваться

Практикум по компьютерной геометрии

Тензоры: опыт создания пользовательского пакета программ

Встроенные возможности Mathematica для работы с тензорами

Списки, соответствующие тензорам

Создание таблиц

Вопросы и ответы