Тензоры: опыт создания пользовательского пакета программ

Функции для работы с таблицами

Как мы уже выясняли в прошлом семестре, в Mathematica имеется ряд команд, манипулирующих списками. К наиболее популярным из них относятся команды, имена которых начинаются с Map: Map, MapThread, MapIndexed и др. Команда Map настолько широко используется, что для нее была придумана специальная форма, а именно, f /@ list (этой формой записи команды Map мы будем пользоваться многократно):

In[26]:=Map[f [#] &, {{а, b}, {с, d}}] 
           f[#] &/@{{a, b}, {с, d}} 
           MapThread[f[#l, #2, #3] &,
            {{{a}, {b}}, {{c}, {d}}, {{e}, {f}}}]
               (* #l соответствует элементам
               первого списка, #2 - второго и т.д.*) 
             MapIndexed[f [#1] [#2] &, {{а, b} , {с, d} } ] 
               (* #2 соответствует номеру текущего
                 элемента списка взятого в фигурные скобки *)
Out[26]={f [{a, b}], f [{с, d}]} 
Out[27]={f [{a, b}], f [{с, d}]} 
Out[28]={f[{a}, {с}, {е}], f[{b}, {d}, {f}]} 
Out[29]={f [{a, b}] [{1}], f[{c, d}] [{2}]}

Эти команды допускают явное указание уровня списка, к элементам которого и нужно применять функцию:

In[30]:=Map[f [#] &, {{а, b} , {с, d} } , {2}] 
           MapThread [ f [ #l, #2, #3] &, 
                 {{{a}, {b}}, {{c}, {d}}, 
               {{e}, {f}}}, 2] 
             (* #l соответствует элементам 
               первого списка, #2 - второго и т.д.*) 
             MapIndexedff[#1][#2] &,
                 {{а, b}, {с, d}}, {2}] 
           (* #2 соответствует номеру 
                 текущего элемента списка, 
               взятого в фигурные скобки *)
Out[30]={{f [a], f [b]}, {f [с], f [d]}}
Out[3l]={{f [а, с, e]}, {f[b, d, f ]}}
Out[32] = 
         {{f[a] [{1, 1}], f[b] [{1, 2}] }, {f[c] [{2, 1}], f[d] [{2, 2}]}}

Заметьте, что теперь номер текущего элемента является списком длины 2. Такая общность интерпретации команды MapIndexed и объясняет, почему номер элемента берется в фигурные скобки.

Следующая команда Tuples строит или n -кратное декартово произведение списка на себя:

In[33] := Tuples [{а, b, с}, 3]
Out[33] =
       {{а, а, а},{а,а, b},{а, а, с},{a, b, a},{a,b, b}, {а, b, с},
        {а, с, а},{а,с, b},{а, с, с},{b, a, a},{b,a, b}, {b, а, с},
        {b, b, а},{b,b, b},b, b, с},{b, с, а},{b,с, b},
        {b, с, с},{с,а, а},{с, а, b},{с, а, с},{с,b, а},
        {с, b, b},{с,b, с},{с, с, а},{с, с, b},{с,с, с}}

или, более общо, декартово произведение списков:

In[34]:= Tuples [{{a1, a2 } , {b1, b2 , b3}, {c1, c2}}]
Out[34] = {{a1, b1, c1}, {a1, b1, c2 }, {a1, b2 , c1}, {a1, b2, c2 }, 
           {a1, b3, c1}, {a1, b3, c2}, {a2, b1, c1}, {a2, b1, c2}, 
           {a2, b2, c1}, {a2, b2, c2}, {a2, b3, c1}, {a2, b3, c2}}

Наконец, еще две очень популярные команды: Outer и Inner, являющиеся обобщениями тензорного произведения и свертки тензоров (в частности, скалярного произведения).

Команда Outer[f,list1,list2,...] применяет произвольную функцию f к всевозможным комбинациям элементов списков list1,list2,...:

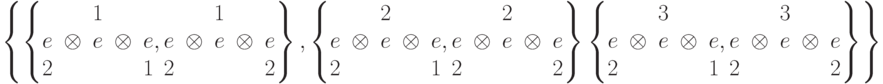
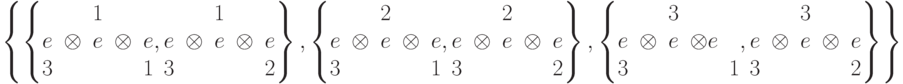
Команда Inner[f,list1,list2,g] обобщает команду Dot[] (или ".")

In[36]:={a, b, с} . {х, у, z}
Out[36] =ax+by+cz

причем f играет роль умножения, а g - сложения:

In[37] := Inner [Min, {а, b, с}, {х, у, z}, Max]
          Inner [CircleTimes, {a, b, с}, {х, у, z}, Plus]
Out[37]=Max [Min [a, x] , Min[b, у], Min [с, z] ]

Тензорные поля

В курсе дифференциальной геометрии, тензоры используются для изучения многообразий и порождают тензорные поля, т. е. тензоры одного и того же типа, заданные на касательных пространствах к многообразию. Теперь базисы в этих линейных пространствах выбираются исходя из локальных координат, а тензорный закон, как следствие, использует матрицу Якоби перехода от одной системы координат к другой. Таким образом, чтобы получить координатное представление тензорного поля, нужно вместо базисов еь ..., е" брать локальные координаты 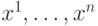, вместо чисел 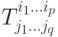- функции 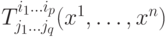, а тензорный закон писать с использованием матриц Якоби.

Пример создания пакета для работы с тензорами

Опишем разработанный нами пакет для работы с тензорами. Мы приведем здесь лишь небольшую часть того, что необходимо при работе с тензорами и тензорными полями. Наш центральный принцип - сделать работу с тензорами наиболее наглядной. Чтобы загрузить наш пакет, следует выполнить команду

In[39] =Needs ["Tensors " " , NotebookDirectory [ ] <> "tensors.m"]

где второй аргумент - это имя файла, в котором пакет содержится. (Здесь мы предполагаем, что пакетный файл tensors.m расположен в той же папке, что и файл, с которым вы сейчас работаете, причем ваш файл или был открыт, уже находясь в указанной папке, или был сохранен в ней, иначе значение функции NotebookDirectory[] не определено.)

Правила работы в пакете Tensors

В данном разделе мы опишем возможности текущей версии пакета. Разумеется, их можно и нужно расширять.

Начало работы, создание базиса и тензоров, тензорные операции.

В пакете реализованы возможности работы как с алгебраическими тензорами (т. е. тензорами в линейном пространстве), так и с тензорными полями (в последнем случае, в текущей версии пакета, тензорные поля рассматриваются на многообразии, состоящем из одной карты, т. е. на области в 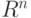). Чтобы начать работу в пакете, следует задать или базис линейного пространства (функция makeBasis ), или локальные координаты и соответствующий канонический базис (функция makeBasisDif). Чтобы посмотреть формат интересующей вас функции пакета, следует выполнить команду ?<имя функции>. Например:

In40] := ? makeBasis

Зададим базис в трехмерном пространстве.

In[41] :=makeBasis [e, 3]

Все создаваемые базисы последовательно нумеруются. Номер текущего базиса записывается в переменную curBas, а сам базис - в список базисов basis:

In[42] := curBas
          basis[curBas] 
          val[e] 
          basis[1]
Out[42] = 1

Отметим, что на самом деле команда создает также двойственный базис. Обратите внимание, что мы пишем индексы непосредственно над и под буквами (а не справа вверху и справа внизу). Это объясняется тем, что правый верхний индекс Mathematica воспринимает как степень. Набирать такие индексы удобно с помощью сочетаний клавиш Ctrl+= для нижнего индекса и Ctrl+7 для верхнего индекса. Если же требуется поставить одновременно верхний и нижний индексы, то следует набрать одновременно Ctrl+= +5.

После того как базис фиксирован, можно создать тензор любого типа. При этом предусмотрена возможность задать абстрактный тензор с неопределенными компонентами ( makeTensor ) и возможность задать тензор с конкретными значениями компонент ( makeTensorTab ):

In[46] =makeTensor [T, 1, 1] ; makeTensorTab [W, {2, b, с}, 1, 0] ;

Чтобы посмотреть значения компонент тензора, надо выполнить команду val:

In[47] : = val[T] 
           val[W]

Out[48] = {2, b, c}

Над заданными тензорами можно выполнять тензорные операции. Реализованы линейная комбинация, тензорное произведение, свертка, перестановка индексов, симметрирование, альтернирование.

Значок тензорного произведения можно получить, набрав Esc c* Esc :

Линейная комбинация допустима только для тензоров одного типа:

Результат применения тензорных операций можно присвоить с помощью обычного оператора Set (т. е. =):

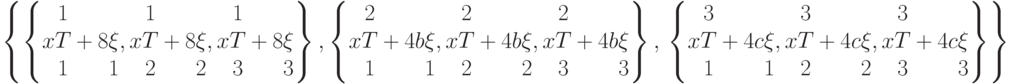
Свертка записывается просто указанием номеров индексов, по которым надо сворачивать:

Перестановка индексов указывается в виде списка, элементы которого суть -образы последовательных натуральных чисел начиная с 1. При этом список заключается в дополнительные фигурные скобки и пишется сверху или снизу, в зависимости от того, какие индексы мы собираемся переставлять: