Работа с графикой: визуализация функций одной переменной
6.4. Комбинирование рисунков
Пусть мы построили один или несколько двумерных графиков. В процессе работы с изображением может возникнуть ситуация, когда графический стиль изображения следует изменить. Однако вычисления, связанные с построением графиков, могут быть весьма ресурсоёмкими. Поэтому Mathematica позволяет изменить стиль изображения без повторного вычисления зависимости: для этих целей в программе имеется функция Show. Заданная в форме Show[pict] она заново рисует ранее построенный рисунок pict с прежними установками, ничего в рисунке не меняя. Для того чтобы изменить установки графических опций, при которых был построен рисунок, следует задать функцию в виде Show[pict,option1->val1,option2->val2,...]: каждой опции option задаётся значение val.
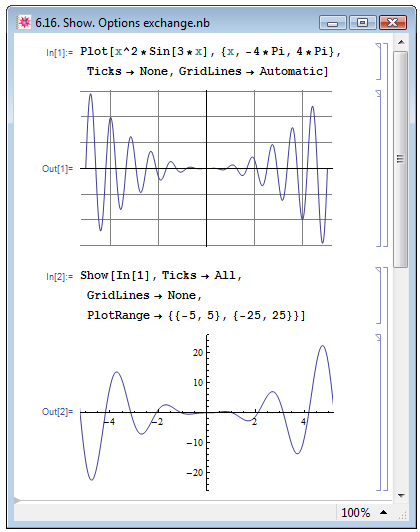
В примере In[1] на рис. 6.16 при помощи функции Plot мы построили график некоторой функции x^2*Sin[3*x] от переменной x. При построении мы избавились от меток на осях, Ticks->None, а на график набросили координатную сетку, GridLines->Automatic. В примере In[2] мы решили перестроить наш рисунок, воспользовавшись функцией Show, и вернули метки на координатные оси, Ticks->All, от линий сетки избавились, GridLines->None, а на экран вывели лишь центральную область изображения, PlotRange->{{-5,5},{-25,25}}.
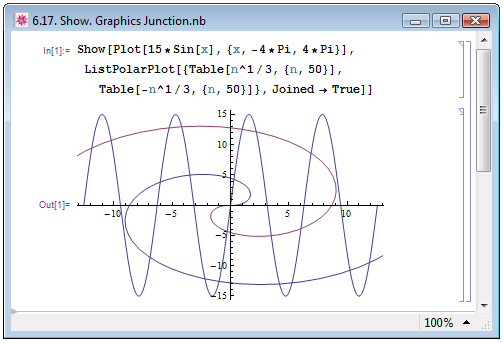
Выражение Show[plot1,plot2,...] при вычислении объединяет несколько графиков в один, причём функции для построения рисунков не обязательно должны быть одинаковыми. Согласование по координатам происходит автоматически. На рис. 6.17 мы совместили на одном рисунке графики, построенные в отдельности друг от друга при помощи функций Plot и ListPolarPlot.
Подробней о функции Show см. книгу Е. М. Воробьёва [1, с. 87–88].
6.5. Двумерные графические примитивы и директивы
По большому счёту, изображения, создаваемые функциями Plot, ListPlot и остальные им подобные, конструируются из точек, связанных друг с другом линиями, а особенности представления изображений задаются опциями, которые либо имеют значения по умолчанию, либо явно заданы пользователем. Для того чтобы проникнуть в "таинство" построения графиков, воспользуемся подходом С. Мангано [11, с. 238], а именно, познакомимся с внутренним представлением функции Plot при построении некоторой зависимости.
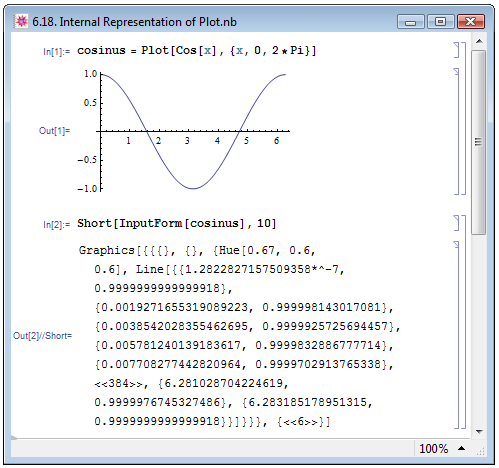
Построим в качестве примера (In[1] на рис. 6.18) зависимость математической функции Cos[x] от её аргумента x, на отрезке от 0 до 2*Pi, для чего зададим функцию в виде Plot[Cos[x],{x,0,2*Pi}]. Чтобы узнать, в каком виде Mathematica обрабатывает эту функцию, применим к ней InputForm. Внутренние данные представляют собой вложенный список с достаточно большим количеством элементов. Чтобы не загромождать экран, воспользуемся функцией Short[expr,n], которая выводит данные выражения expr в сокращённой форме на n строк. В примере In[2] мы выводим внутреннюю форму функции Plot[Cos[x],{x,0,2*Pi}] в сокращённом виде на 10 строк. В Out[2] мы видим, что рисунок состоит из последовательности координат (или точек на плоскости), лежащих на одной линии Line. Для семи точек координаты показаны, а для 384 остальных скрыты, "384". Цвет линии графика задан как Hue[0.67,0.6,0.6]. Последний элемент в списке Out[2], {"6"}, указывает на остальные использованные при построении опции, которые в данном примере оказались опущены. Используемый для построения рисунка конструктивный элемент Line (линия), с которым мы познакомились в предыдущем примере, является графически примитивом. Под графическими примитивами понимаются минимальные графические объекты, которые составляют рисунок.
Таким образом, все рисунки, строящиеся в Mathematica, состоят из графических примитивов.
В двумерной графике используются такие примитивы, как точка (point), линия (line), прямоугольник (rectangle), многоугольник (polygon), дуга (circle), диск (disk), текст (text).
Точка — это выражение вида Point[{x,y}], где х и у — декартовы координаты точки на плоскости.
Линия — это ломаная линия, состоящая из отрезков прямых, последовательно соединяющих точки: Line[{{x1,y1},{x2,y2},...}]. Используя именно этот примитив, Mathematica построила рисунок в Out[1] на рис. 6.18.
Графический примитив многоугольник, задаваемый функцией Polygon[{{x1,y1},{x2,y2},...}], представляет собой многоугольник с заполнением, ограниченный замкнутой ломаной линий, проходящей через точки {x1,y1},{x2,y2},....
Частный случай многоугольника — прямоугольник. Для создания прямоугольника, стороны которого параллельны осям координат, в Mathematica имеется специальный примитив Rectangle[{xleftdown,уleftdown},{xrightup,yrightup}], где {xleftdown,уleftdown} — координаты левого нижнего угла, а {xrightup,yrightup} — правого верхнего.
Примитив Circle[{x,y},r] рисует окружность радиуса r с центром в точке {x,y}.
За изображение дуги окружности отвечает тот же примитив, но с расширенным набором аргументов: Circle[{x,y},r,{ang1,ang2}], где первый аргумент {x,y} указывает координаты центра окружности, которой принадлежит дуга, второй аргумент r — радиус окружности, а {ang1,ang2} — полярные углы, обозначающие начальную и конечную точку дуги.
Тот же примитив, заданный в следующем виде Circle[{x, y},{rx,ry}], рисует эллипс с полуосями rx и ry и с центром всё в той же точке {x,y}
Полностью закрашенный круг получается при помощи примитива Disk[{x,y},r].
Другой графический примитив Text[expr,{x,y}], где expr — некоторое выражение, выводит печатную форму выражения expr и центрирует его относительно точки {x,y}.
Если мы введём выражения для задания примитивов в окно ввода в Mathematica и запустим вычисления, то наши ожидания увидеть на экране рисунок, не оправдаются. Для того чтобы превратить примитив в рисунок на экране, нужно применить к нему функцию Graphic.
Подробней о двумерных графических примитивах Mathematica см. в книгах Е. М. Воробьёва [1, с. 92–96] и Ч. Гетца и Дж. Хелмстедт [9, с. 28–35].
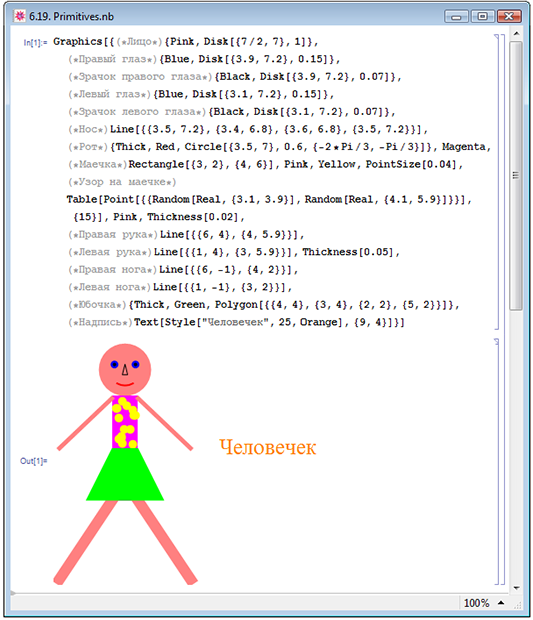
На рисунке 6.19 мы при помощи примитивов схематично изобразили человечка. Лицо и глаза мы построили при помощи примитива Disc, нос, ручки и ножки — при помощи примитива Line, рот — примитива Circle, тело — Rectangle, узор на маечке — Point, юбочку — Polygon. Также мы подписали наш рисунок, Text[Style["Человечек",25,Orange],{9,4}], изменив стиль текста при помощи функции Style.
Однако на рисунке 6.19 не все примитивы изображены одинаковым образом: в нашем примере они отличаются друг от друга цветом и толщиной линии. С директивами для изменения цвета мы уже познакомились выше: RGBColor[d1,d2,...] и Hue[d1,d2,...], равно как и с директивой изменения относительной толщины линии Thickness[d].
Другие директивы для работы с графическими примитивами следующие.
PointSize[r] — определяет относительный размер точки как круга радиуса r. При этом r есть отношении радиуса к полной ширине рисунка.
Директива Dashing[{rl,r2,...}] представляет линию в виде последовательности отрезков длины r1, r2 и т.д., которые повторяются периодически. Этой директивой можно преобразовывать сплошную линию в штриховую или штрихпунктирную.
Для того чтобы директива была применена к некоторому примитиву, она должна ставиться перед этим примитивом. Чтобы ограничить действие директивы на один или несколько примитивом, нужно заключить эту директиву и требуемые примитивы в фигурные скобки. Если на примитив действует сразу несколько директив, то все они должны стоять перед этим примитивом.
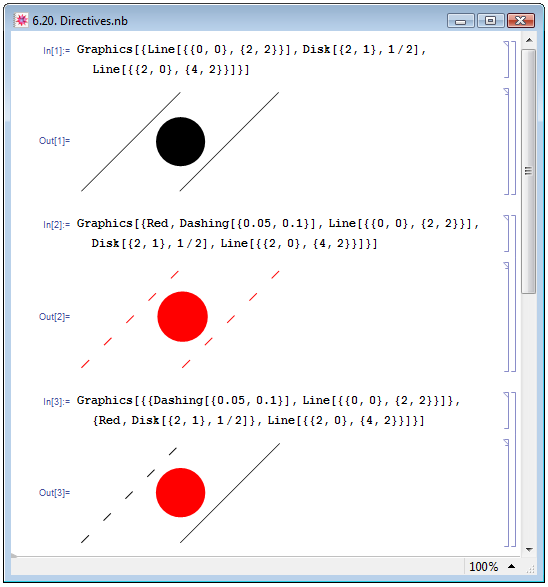
В примере In[1] на рис. 6.20 мы изобразили последовательно отрезок линии Line[{{0,0},{2,2}}], заполненный круг Disk[{2,1},1/2] и ещё один отрезок Line[{{2,0},{4,2}}]. При этом мы не использовали дополнительных графических директив. В примере In[2] на том же рисунке мы поставили впереди всех примитивов директивы изменения цвета на красный Red, изменили тип линий на штриховой Dashing[{0.05,0.1}]. Поскольку мы не использовали дополнительных фигурных скобок, то указанные директивы оказались применены ко всем примитивам. В примере In[3] мы применили директиву изменения типа линии на штриховой только к первому примитиву, заключив оба этих объекта в фигурные скобки, а "покрасили" только второй примитив, переместив директиву Red в соответствующее место и также заключив оба объекта в фигурные скобки.
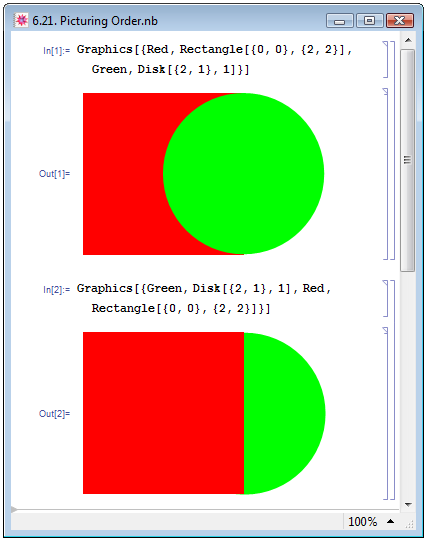
Что касается очерёдности изображений, вызываемых применением примитивов: сверху оказывается изображение того примитива, который указан в графической функции позже. На рис. 6.21 мы изобразили накладывающиеся друг на друга красный квадрат Red,Rectangle[{0,0},{2,2}] и зелёный круг Green,Disk[{2,1},1]. В примере In[1] последним мы указали примитив Disk[{2,1},1], потому круг оказался на переднем плане. В примере In[2] мы поменяли примитивы местами, поэтому на переднем плане оказался квадрат.
Ключевые термины
Под графическими директивами понимаются выражения, влияющие на характеристики графических объектов.
Под графическими примитивами понимаются минимальные графические объекты, которые составляют рисунок.
Краткие итоги
В данной лекции мы познакомились с основными встроенными функциями Mathematica для визуализации зависимостей одной величины от другой. В частности мы научились строить графики непрерывных функций одной переменной, дискретных зависимостей одной величины от другой, мы научились визуализировать параметрические зависимости. Мы научились совмещать графики зависимостей, построенные различными способами, на одном рисунке. Мы познакомились с основными опциями графических функций и научились с их помощью изменять внешний вид рисунков. Мы познакомились с двумерными графическими примитивами, правилами их задания и применения. Мы познакомились с графическими директивами и научились применять их в сочетании с опциями графических функций и правилами задания примитивов для изменения внешнего вида изображений.
Вопросы
- Какое выражение содержится в заголовке всех функций Mathematica, предназначенных для работы с двумерной графикой?
- Назовите функции Mathematica, предназначенные для визуализации непрерывных математических зависимостей. Какие аргументы они содержат?
- Назовите графическую опцию функции построения двумерных объектов и способы её задания, использующуюся для
- управления способом отображения линий графиков;
- задания координат пересечения осей на рисунке;
- набрасывания на изображение координатной сетки;
- задания отношения ширины рисунка к его высоте;
- управления наличием на рисунке координатных осей;
- управления способом отображения координатных осей;
- управления расстановкой координатных отметок на координатных осях;
- задания подписей к координатным осям;
- заключения изображения в прямоугольную рамку;
- управления способом отображения рамки;
- задания подписей к сторонам рамки;
- управления расстановкой координатных отметок на сторонах рамки;
- выбора области зависимости, которую следует отобразить на изображении;
- заполнения цветом некоторой обозначенной на изображении области.
- Назовите функции Mathematica, предназначенные для визуализации дискретных зависимостей. Какие аргументы они содержат?
- Для каких целей предназначены специфические для функций визуализации дискретных зависимостей опции Joined и InterpolationOrder? Каким образом они задаются?
- Каким образом можно совместить на одном рисунке несколько изображений, полученных при помощи разных функций?
- Каким образом можно изменить стиль отображения уже построенных графиков, повторно их не перестраивая?
- Что понимают под графическими примитивами?
- Назовите функции построения следующих графических примитивов с соответствующими аргументами: точка, линия, прямоугольник, многоугольник, дуга, диск, текст.
- Что понимают под графическими директивами?
- Какой функцией Mathematica необходимо воспользоваться, чтобы создать на экране изображение примитива?
- Для каких целей предназначены графические директивы RGBColor, Hue, Thickness, PointSize, Dashing? Какие аргументы они содержат?
Упражнения
- На одном рисунке постройте графики функций
 и
и 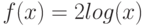 на интервале от
на интервале от  до
до 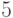 , окрасьте первый график в красный цвет, а второй — в синий. Заполните пространство между кривыми зелёным цветом в области, когда
, окрасьте первый график в красный цвет, а второй — в синий. Заполните пространство между кривыми зелёным цветом в области, когда 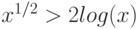 , и оранжевым цветом, когда
, и оранжевым цветом, когда 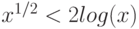 .
. - Постройте совместный график функции
 и её производной по
и её производной по  на интервале от
на интервале от  до
до  . Создайте ещё одно изображение, содержащее фрагмент построенных зависимостей на интервале
. Создайте ещё одно изображение, содержащее фрагмент построенных зависимостей на интервале  от
от 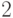 до
до 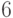 и
и  от
от 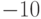 до
до  . Сделайте линию графика функции штрихпунктирной, а линию графика производной — штриховой. Набросьте на изображение координатную сетку.
. Сделайте линию графика функции штрихпунктирной, а линию графика производной — штриховой. Набросьте на изображение координатную сетку. - Постройте параметрическую зависимость заданной в предыдущем пункте функции от её производной на интервале изменения
 от 0 до 50. Перенесите пересечение координатных осей в точку с координатами (-2500,2500). Удалите с рисунка координатные оси и заключите изображение в рамку.
от 0 до 50. Перенесите пересечение координатных осей в точку с координатами (-2500,2500). Удалите с рисунка координатные оси и заключите изображение в рамку. - Постройте дискретную зависимость функции
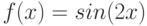 для
для  , принимающего значения от 0 до 10 с шагом 0.2 при помощи функции DiscretePlot.
, принимающего значения от 0 до 10 с шагом 0.2 при помощи функции DiscretePlot.
Постройте такую же зависимость при помощи функции ListPlot. Для этого предварительно при помощи функции Table создайте список, содержащий значения переменной x и соответствующие им значения функции
 .
.Задайте опции Joined, InterpolationOrder и Filling так, чтобы
- они принимали для обоих графиков одинаковые значения;
- для разных графиков они принимали разные значения.
-
- используя примитив Disk, создайте 7 вложенных кругов с одними координатами центра и радиусами от 1 до 7. Пользуясь соответствующими директивами, окрасьте их в цвета радуги.
- поменяв порядок вызова примитивов, оставьте на рисунке только фиолетовый, голубой, жёлтый и красный круги.
- выстройте круги в одну линию в произвольном порядке, чтобы они соприкасались друг с другом.
- выстройте круги в одну линию от самого большого к самому маленькому так, чтобы центр меньшего круга лежал на границе большего, и меньший круг не закрывался большим.
- При помощи графических примитивов создайте изображения следующих дорожных знаков: "светофорное регулирование", "опасный поворот направо", "крутой подъём", "главная дорога", "движение без остановки запрещено", "въезд запрещён", "остановка запрещена", "стоянка запрещена по нечётным числам месяца", "объезд препятствия справа", "искусственная неровность", "тупик", "место стоянки".