Интеллектуальные задачи в экономике
Нечёткие нейронные сети
Нечёткие нейронные сети (fuzzy-neural networks) осуществляют выводы на основе аппарата нечёткой логики, однако параметры функций принадлежности настраиваются с использованием алгоритмов обучения нейронных сетей (НС). Поэтому для подбора параметров таких сетей применим метод обратного распространения ошибки, изначально предложенный для обучения многослойного персептрона. Для этого модуль нечёткого управления представляется в форме многослойной сети. Нечёткая нейронная сеть, как правило, состоит из четырех слоёв: слоя фазификации входных переменных, слоя агрегирования значений активации условия, слоя агрегирования нечётких правил и выходного слоя.
Наибольшее распространение в настоящее время получили архитектуры нечёткой НС вида ANFIS и TSK. Доказано, что такие сети являются универсальными аппроксиматорами.
Быстрые алгоритмы обучения и интерпретируемость накопленных знаний – эти факторы сделали сегодня нечёткие нейронные сети одним из самых перспективных и эффективных инструментов мягких вычислений.
Адаптивные нечёткие системы
Классические нечёткие системы обладают тем недостатком, что для формулирования правил и функций принадлежности необходимо привлекать экспертов той или иной предметной области, что не всегда удаётся обеспечить. Адаптивные нечёткие системы (adaptive fuzzy systems) решают эту проблему. В таких системах подбор параметров нечёткой системы производится в процессе обучения на экспериментальных данных. Алгоритмы обучения адаптивных нечётких систем относительно трудоёмки и сложны по сравнению с алгоритмами обучения нейронных сетей, и, как правило, состоят из двух стадий:
- Генерация лингвистических правил;
- Корректировка функций принадлежности.
Первая задача относится к задаче переборного типа, вторая – к оптимизации в непрерывных пространствах. При этом возникает определённое противоречие: для генерации нечётких правил необходимы функции принадлежности, а для проведения нечёткого вывода – правила. Кроме того, при автоматической генерации нечётких правил необходимо обеспечить их полноту и непротиворечивость.
Значительная часть методов обучения нечётких систем использует генетические алгоритмы. В англоязычной литературе этому соответствует специальный термин – Genetic Fuzzy Systems.
Значительный вклад в развитие теории и практики нечётких систем с эволюционной адаптацией внесла группа испанских исследователей во главе с Ф. Херрера (F. Herrera).
Нечёткие запросы
Нечёткие запросы к базам данных (fuzzy queries) – перспективное направление в современных системах обработки информации. Данный инструмент даёт возможность формулировать запросы на естественном языке, например: "Вывести список недорогих предложений о съёме жилья близко к центру города", что невозможно при использовании стандартного механизма запросов. Для этой цели разработана нечёткая реляционная алгебра и специальные расширения языков SQL для нечётких запросов. Большая часть исследований в этой области принадлежит западноевропейским ученым Д. Дюбуа и Г. Праде.
Нечёткие ассоциативные правила
Нечёткие ассоциативные правила (fuzzy associative rules) – инструмент для извлечения из баз данных закономерностей, которые формулируются в виде лингвистических высказываний. Здесь введены специальные понятия нечёткой транзакции, поддержки и достоверности нечёткого ассоциативного правила.
Нечёткие когнитивные карты
Нечёткие когнитивные карты (fuzzy cognitive maps) были предложены Б. Коско в 1986 г. и используются для моделирования причинных взаимосвязей, выявленных между концептами некоторой области. В отличие от простых когнитивных карт, нечёткие когнитивные карты представляют собой нечёткий ориентированный граф, узлы которого являются нечёткими множествами. Направленные рёбра графа не только отражают причинно-следственные связи между концептами, но и определяют степень влияния (вес) связываемых концептов. Активное использование нечётких когнитивных карт в качестве средства моделирования систем обусловлено возможностью наглядного представления анализируемой системы и с лёгкостью интерпретации причинно-следственных связей между концептами. Основные проблемы связаны с процессом построения когнитивной карты, который не поддаётся формализации. Кроме того, необходимо доказать, что построенная когнитивная карта адекватна реальной моделируемой системе. Для решения данных проблем разработаны алгоритмы автоматического построения когнитивных карт на основе выборки данных.
Нечёткая кластеризация
Нечёткие методы кластеризации, в отличие от чётких методов (например, нейронные сети Кохонена), позволяют одному и тому же объекту принадлежать одновременно нескольким кластерам, но с различной степенью. Нечёткая кластеризация во многих ситуациях более "естественна", чем чёткая, например, для объектов, расположенных на границе кластеров. Наиболее распространены: алгоритм нечёткой самоорганизации c-means и его обобщение в виде алгоритма Густафсона-Кесселя.
Список можно продолжить и дальше: нечёткие деревья решений, нечёткие сети Петри, нечёткая ассоциативная память, нечёткие самоорганизующиеся карты и другие гибридные методы.
11.3. Нейронные сети в экономике
Область ИИ, нашедшая наиболее широкое применение - нейронные сети. Основная их особенность - это способность к самообучению на конкретных примерах.
Нейросети предпочтительны там, где имеется очень много входных данных, в которых скрыты закономерности. Целесообразно использовать нейросетевые методы в задачах с неполной или "зашумлённой" информацией, а также в таких, где решение можно найти интуитивно.
Нейросети применяются для предсказания рынков, оптимизации товарных и денежных потоков, анализа и обобщения социологических опросов, предсказание динамики политических рейтингов, оптимизации производственного процесса, комплексной диагностики качества продукции и для многого, многого другого.
Нейронные сети всё чаще применяются и в реальных бизнес - приложениях. В некоторых областях, таких как обнаружение фальсификаций и оценка риска, они стали бесспорными лидерами среди используемых методов. Их использование в системах прогнозирования и системах маркетинговых исследований постоянно растёт.
Поскольку экономические, финансовые и социальные системы очень сложны и являются результатом действий и противодействий различных людей, то является очень сложным (если не невозможным) создать полную математическую модель с учётом всех возможных действий и противодействий. Практически невозможно детально аппроксимировать модель, основанную на таких традиционных параметрах, как максимизация полезности или максимизация прибыли.
В системах подобной сложности является естественным и наиболее эффективным использовать модели, которые напрямую имитируют поведение общества и экономики. А это как раз то, что способна предложить методология нейронных сетей.
Ниже перечислены области, в которых эффективность применения нейронных сетей доказана на практике:
Для финансовых операций:
- Прогнозирование поведения клиента.
- Прогнозирование и оценка риска предстоящей сделки.
- Прогнозирование возможных мошеннических действий.
- Прогнозирование остатков средств на корреспондентских счетах банка.
- Прогнозирование движения наличности, объёмов оборотных средств.
- Прогнозирование экономических параметров и фондовых индексов.
Для планирования работы предприятия:
- Прогнозирование объёмов продаж.
- Прогнозирование загрузки производственных мощностей.
- Прогнозирование спроса на новую продукцию.
Для бизнес - аналитики и поддержки принятия решений:
- Выявление тенденций, корреляций, типовых образцов и исключений в больших объёмах данных.
- Анализ работы филиалов компании.
- Сравнительный анализ конкурирующих фирм.
Другие приложения:
- Оценка стоимости недвижимости.
- Контроль качества выпускаемой продукции.
- Системы слежения за состоянием оборудования.
- Проектирование и оптимизация сетей связи, сетей электроснабжения.
- Прогнозирование потребления энергии.
- Распознавание рукописных символов, в т.ч. автоматическое распознавание и аутентификация подписи.
- Распознавание и обработка видео - и аудио сигналов.
Нейронные сети могут быть использованы и в других задачах. Основными предопределяющими условиями их использования являются наличие "исторических данных", используя которые нейронная сеть сможет обучиться, а также невозможность или неэффективность использования других, более формальных, методов.
Независимый экспертный совет по стратегическому анализу проблем внешней и внутренней политики при Совете Федерации НИИ искусственного интеллекта представил проект "Технология нового поколения на основе недоопределённых вычислений и её использование для разработки экспериментальной модели макроэкономики РФ". Появилась возможность просчитывать исход любого действия или предложения, касающегося бюджета страны, на много лет вперёд.
Система позволяет видеть, как изменится доходная часть, дефицит бюджета, объём промышленного производства в ответ, скажем, на увеличение налогов. Также можно посмотреть, сколько денег в прошлом году уплыло из бюджета: электронная машина, по уверению учёных, легко сможет справиться и с такой задачей. Ей даже не надо будет объяснять понятие "чёрный нал".
Можно решить и обратную задачу. Например, а что надо сделать, чтобы к 2020 году объём производства увеличился или, скажем, хотя бы не падал? Машина укажет нижнюю и верхнюю границу значений в том и другом случае для отпускаемых бюджетных денег по всем параметрам, так или иначе влияющим на производство.
Кроме того, можно узнать не по гороскопу и без помощи магов возможную последовательность "критических" и "удачных" моментов в развитии экономики страны при заданных исходных данных.
Разработчики проекта создали пока лишь демонстрационную модель, охватывающую около 300 параметров и период от 1990-го до 1999 года. Но для нормальной работы необходимо не менее 1000 параметров. И такая работа может быть проведена, если на неё будут отпущены средства. Надо провести множество прикладных работ, необходимы фундаментальные исследования по обоим основным составляющим проекта - математической и экономической. Здесь нужна серьёзная государственная материальная поддержка.
Внедрение действующей компьютерной модели макроэкономики и госбюджета РФ позволит автоматизировать подготовку исходных параметров госбюджета очередного года, согласование окончательного варианта для утверждения в парламенте, поддержку, оценку и контроль исполнения бюджета на всех его этапах.
Интерес к искусственным нейронным сетям в России очень вырос за последние несколько лет. Возможность быстрого обучения и достоверность выводов позволяет рекомендовать нейросетевые экспертные системы как один из обязательных инструментов во многих аспектах современного бизнеса. Нейронные сети обладают огромным преимуществом перед традиционным трудозатратным и более длительным путём обобщения знаний людей-экспертов.
Технологии нейронных сетей применимы практически в любой области, а в таких задачах, как прогнозирование котировок акций и курса валют они стали уже привычным и широко используемым инструментом. Повсеместное проникновение нейросетевых технологий в современный бизнес - только вопрос времени. Внедрение новых наукоёмких технологий - это процесс сложный, однако практика показывает, что инвестиции не только окупаются и приносят выгоду, но и дают тем, кто их использует, ощутимые преимущества.
Применение нейронных сетей в финансах базируется на одном фундаментальном допущении: замене прогнозирования распознаванием. По большому счёту, нейросеть не предсказывает будущее, а "узнаёт" в текущем состоянии рынка ранее встречавшуюся ситуацию и воспроизводит последовавшую реакцию рынка.
Финансовый рынок достаточно инерционен, у него есть своя определённая "замедленная реакция", зная которую можно довольно точно вычислять грядущую ситуацию. А насколько точно - это зависит от условий рынка и квалификации оператора.
Поэтому наивно верить, что нейросеть будет автоматически предсказывать курсы основных индикаторов — национальной валюты или, например, драгоценных металлов на нестабильных рынках. Но при любой рыночной ситуации существуют инструменты, сохраняющие стабильность. Например, при скачках доллара — это "дальние" фьючерсы, реакция которых растягивается на несколько дней и поддаётся прогнозу. Кстати, в периоды рыночных потрясений игроки обычно паникуют, что усиливает преимущества владельца хорошего аналитического инструмента.
Над созданием нейронных сетей различного назначения в настоящее время трудятся сотни всемирно известных, а также мелких начинающих фирм. Мировой рынок предлагает более сотни нейросетевых пакетов, преимущественно — американских. Общий объём рынка нейронных сетей к 2005 году превысил $10 млрд. И, практически, каждый разработчик традиционных аналитических пакетов сегодня стремится включить нейронные сети в новые версии своих программ. В США нейронные сети применяются в аналитических комплексах каждого крупного банка.
Продажа одного только нейросетевого пакета "Brain Maker Pro" сравнима с объёмами продаж самого популярного пакета технического анализа MetaStock (в США продано более 20000 копий Brain Maker Pro).
Хорошо зарекомендовал себя пакет "The AI Trilogy". ("Трилогия искусственного интеллекта") американской фирмы "Ward Systems Group". Это набор из трёх программ, каждая из которых может использоваться как самостоятельно, так и в комбинации с остальными.
Так, программа "NeuroShell II" — это набор из 16 типов нейронных сетей, "NeuroWindows" — нейросетевая библиотека с исходными текстами, "GeneHunter" — генетическая программа оптимизации. В совокупности они образуют мощный "конструктор", позволяющий строить аналитические комплексы любой сложности.
"The AI Trilogy" на американском рынке пользуется большим спросом. Пакет установлен в 150 крупнейших банках США. Он многократно побеждал в престижных конкурсах популярных финансовых изданий и помогает управлять капиталами в несколько миллиардов долларов. Фирма "Du Pont" (институт стандартов США и ФБР) считает "Трилогию искусственного интеллекта" лучшей для решения различных задач.
Интересен и знаменателен малоизвестный факт, что ключевые компоненты этого пакета были написаны российскими программистами. Своим обликом пакет обязан группе разработчиков из небольшой московской компании "Нейропроект" под руководством профессора Персиянцева. Она более трёх лет выполняла заказы фирмы "Ward Systems Group" и нашла удачные решения. Можно сказать, что русские программы управляют финансами Америки и задачами ФБР!
Насколько может быть полезен пакет финансистам? В состоянии ли он будет работать на нашем непредсказуемом рынке, где одно решение Центробанка может мгновенно опрокинуть рынок? Предваряя эти вопросы, владельцы пакета предлагают специальную консалтинговую услугу.
С банком, аналитики которого не верят в прогнозируемость нашего рынка, заключается специальный договор. В течение определённого периода: две недели, месяц или больше, за символическую плату банку ежедневно предоставляются прогнозы на завтрашний день (или на неделю вперед) по котировкам заданных финансовых инструментов. Если прогноз стабильно демонстрирует приемлемую точность, то банк обязуется купить аналитический комплекс вместе с настройками.
И не было ни единого случая, когда клиент отказывался от покупки. Показательный и впечатляющий случай имел место между выборами, когда один из крупных банков проводил подобное тестирование пакета. Плясали курсы бумаг, падали и поднимались политики, но каждый вечер банк получал прогноз с набором завтрашних цен (мини – макси – средневзвешенная – закрытие) по шестнадцати бумагам ГКО. Не прошло и двух недель, как банк заключил договор на поставку аналитического комплекса, способного сохранять работоспособность даже в таких бурных и непредсказуемых ситуациях.
- Богатые возможности. Нейронные сети - исключительно мощный метод моделирования, позволяющий воспроизводить чрезвычайно сложные зависимости. В частности, нейронные сети нелинейны по свой природе. На протяжении многих лет линейное моделирование было основным методом моделирования в большинстве областей, поскольку для него хорошо разработаны процедуры оптимизации. В задачах, где линейная аппроксимация неудовлетворительна (а таких достаточно много), линейные модели работают плохо. Кроме того, нейронные сети справляются с "проклятием размерности", которое не позволяет моделировать линейные зависимости в случае большого числа переменных
- Простота в использовании. Нейронные сети учатся на примерах. Пользователь нейронной сети подбирает представительные данные, а затем запускает алгоритм обучения, который автоматически воспринимает структуру данных. При этом от пользователя, конечно, требуется какой-то набор эвристических знаний о том, как следует отбирать и подготавливать данные, выбирать нужную архитектуру сети и интерпретировать результаты, однако уровень знаний, необходимый для успешного применения нейронных сетей, гораздо скромнее, чем, например, при использовании традиционных методов статистики.
Нейронные сети привлекательны с интуитивной точки зрения, ибо они основаны на примитивной биологической модели нервных систем. В будущем развитие таких нейробиологических моделей может привести к созданию действительно мыслящих компьютеров. Между тем уже "простые" нейронные сети, которые строит система ST Neural Networks, являются мощным оружием в арсенале специалиста по прикладной статистике.
Параллели из биологии
Нейронные сети возникли из исследований в области искусственного интеллекта, а именно, из попыток воспроизвести способность биологических нервных систем обучаться и исправлять ошибки, моделируя низкоуровневую структуру мозга (Patterson, 1996). Основной областью исследований по искусственному интеллекту в 60-е - 80-е годы были экспертные системы. Такие системы основывались на высокоуровневом моделировании процесса мышления (в частности, на представлении, что процесс нашего мышления построен на манипуляциях с символами). Скоро стало ясно, что подобные системы, хотя и могут принести пользу в некоторых областях, не ухватывают некоторые ключевые аспекты человеческого интеллекта. Согласно одной из точек зрения, причина этого состоит в том, что они не в состоянии воспроизвести структуру мозга. Чтобы создать искусственный интеллект, необходимо построить систему с похожей архитектурой.
Мозг состоит из очень большого числа (приблизительно 10,000,000,000) нейронов, соединённых многочисленными связями (в среднем несколько тысяч связей на один нейрон, однако это число может сильно колебаться).
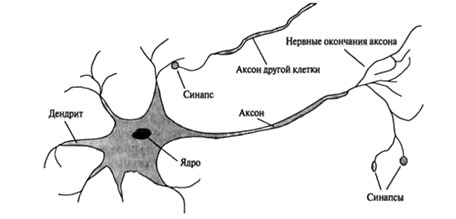
Нейроны - это специальные клетки, способные распространять электрохимические сигналы (рис.11.7).
Нейрон имеет разветвлённую структуру ввода информации (дендриты), ядро и разветвляющийся выход (аксон). Аксоны клетки соединяются с дендритами других клеток с помощью синапсов. При активации нейрон посылает электрохимический сигнал по своему аксону. Через синапсы этот сигнал достигает других нейронов, которые могут, в свою очередь, активироваться. Нейрон активируется тогда, когда суммарный уровень сигналов, пришедших в его ядро из дендритов, превысит определённый уровень (порог активации).
Интенсивность сигнала, получаемого нейроном (а, следовательно, и возможность его активации), сильно зависит от активности синапсов. Каждый синапс имеет протяженность, и специальные химические вещества передают сигнал вдоль него. Один из самых авторитетных исследователей нейросистем, Дональд Хебб, высказал постулат, что обучение заключается, в первую очередь, в изменениях "силы" синоптических связей. Например, в классическом опыте Павлова каждый раз непосредственно перед кормлением собаки звонил колокольчик, и собака быстро научилась связывать звонок колокольчика с пищей. Синоптические связи между участками коры головного мозга, ответственными за слух, и слюнными железами усилились, и при возбуждении коры звуком колокольчика у собаки начиналось слюноотделение.
Таким образом, будучи построен из очень большого числа совсем простых элементов (каждый из которых берёт взвешенную сумму входных сигналов и в случае, если суммарный вход превышает определённый уровень, передаёт дальше двоичный сигнал), мозг способен решать чрезвычайно сложные задачи. Разумеется, здесь не затронуто многих сложных аспектов устройства мозга, однако интересно то, что искусственные нейронные сети способны достичь замечательных результатов, используя модель, которая ненамного сложнее, чем описанная выше.
Базовая искусственная модель
Чтобы отразить суть биологических нейронных систем, определение искусственного нейрона даётся следующим образом:
- Он получает входные сигналы (исходные данные либо выходные сигналы других нейронов нейронной сети) через несколько входных каналов. Каждый входной сигнал проходит через соединение, имеющее определённую интенсивность (или вес); этот вес соответствует синоптической активности биологического нейрона. С каждым нейроном связано определённое пороговое значение. Вычисляется взвешенная сумма входов, из неё вычитается пороговое значение, и в результате получается величина активации нейрона (она также называется пост - синоптическим потенциалом нейрона - PSP).
- Сигнал активации преобразуется с помощью функции активации (или передаточной функции), и в результате получается выходной сигнал нейрона.
При этом используется ступенчатая функция активации (т.е. выход нейрона равен нулю, если вход отрицательный, и единице, если вход нулевой или положительный). Такой нейрон будет работать точно так же, как описанный выше естественный нейрон (вычесть пороговое значение из взвешенной суммы и сравнить результат с нулем - это то же самое, что сравнить взвешенную сумму с пороговым значением). В действительности пороговые функции редко используются в искусственных нейронных сетях. Веса могут быть отрицательными, - это значит, что синапс оказывает на нейрон не возбуждающее, а тормозящее воздействие (в мозге присутствуют тормозящие нейроны).
Это было описание отдельного нейрона. Теперь возникает вопрос: как соединять нейроны друг с другом? Если сеть предполагается для чего-то использовать, то у неё должны быть входы (принимающие значения интересующих нас переменных из внешнего мира) и выходы (прогнозы или управляющие сигналы). Входы и выходы соответствуют сенсорным и двигательным нервам - например, соответственно, идущим от глаз и в руки. Кроме этого, однако, в сети может быть ещё много промежуточных (скрытых) нейронов, выполняющих внутренние функции. Входные, скрытые и выходные нейроны должны быть связаны между собой.
Ключевой вопрос здесь - обратная связь (Haykin, 1994). Простейшая сеть имеет структуру прямой передачи сигнала: сигналы проходят от входов через скрытые элементы и в конце концов приходят на выходные элементы. Такая структура имеет устойчивое поведение. Если же сеть рекуррентная (т.е. содержит связи, ведущие назад от более дальних к более ближним нейронам), то она может быть неустойчива и иметь очень сложную динамику поведения. Рекуррентные сети представляют большой интерес для исследователей в области нейронных сетей, однако при решении практических задач, по крайней мере, до сих пор, наиболее полезными оказались структуры прямой передачи, и именно такой тип нейронных сетей моделируется в пакете ST Neural Networks.
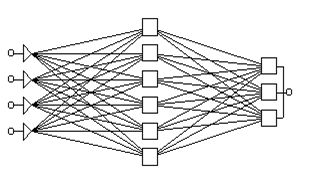
Типичный пример сети с прямой передачей сигнала показан на рис.11.8.
Нейроны регулярным образом организованы в слои. Входной слой служит просто для ввода значений входных переменных. Каждый из скрытых и выходных нейронов соединён со всеми элементами предыдущего слоя.
Можно было бы рассматривать сети, в которых нейроны связаны только с некоторыми из нейронов предыдущего слоя; однако, для большинства приложений сети с полной системой связей предпочтительнее, и именно такой тип сетей реализован в пакете ST Neural Networks.
При работе (использовании) сети во входные элементы подаются значения входных переменных, затем последовательно отрабатывают нейроны промежуточных и выходного слоев. Каждый из них вычисляет своё значение активации, беря взвешенную сумму выходов элементов предыдущего слоя и вычитая из неё пороговое значение. Затем значения активации преобразуются с помощью функции активации, и в результате получается выход нейрона. После того, как вся сеть отработает, выходные значения элементов выходного слоя принимаются за выход всей сети в целом.
Применение нейронных сетей
В предыдущем разделе в несколько упрощенном виде было описано, как нейронная сеть преобразует входные сигналы в выходные. Теперь возникает следующий важный вопрос: как применить нейронную сеть к решению конкретной задачи?
Класс задач, которые можно решить с помощью нейронной сети, определяется тем, как сеть работает и тем, как она обучается. При работе нейронная сеть принимает значения входных переменных и выдаёт значения выходных переменных. Таким образом, сеть можно применять в ситуации, когда у Вас имеется определённая известная информация, и Вы хотите из неё получить некоторую пока не известную информацию (Patterson, 1996; Fausett, 1994). Вот некоторые примеры таких задач:
Прогнозирование на фондовом рынке. Зная цены акций за последнюю неделю и сегодняшнее значение индекса FTSE, спрогнозировать завтрашнюю цену акций.
Предоставление кредита. Требуется определить, высок ли риск предоставления кредита частному лицу, обратившемуся с такой просьбой. В результате разговора с ним известен его доход, предыдущая кредитная история и т.д.
Управление. Нужно определить, что должен делать робот (повернуться направо или налево, двигаться вперёд и т.д.), чтобы достичь цели; известно изображение, которое передаёт установленная на роботе видеокамера.
Разумеется, вовсе не любую задачу можно решить с помощью нейронной сети. Если Вы хотите определить результаты лотереи, тираж которой состоится через неделю, зная свой размер обуви, то едва ли это получится, поскольку эти вещи не связаны друг с другом. На самом деле, если тираж проводится честно, то не существует такой информации, на основании которой можно было бы предсказать результат. Многие финансовые структуры уже используют нейронные сети или экспериментируют с ними с целью прогнозирования ситуации на фондовом рынке, и похоже, что любой тренд, прогнозируемый с помощью нейронных методов, всякий раз уже бывает "дисконтирован" рынком, и поэтому (к сожалению) эту задачу тоже вряд ли удастся решить.
Итак, мы приходим ко второму важному условию применения нейронных сетей: необходимо знать (или хотя бы иметь серьёзные подозрения), что между известными входными значениями и неизвестными выходами имеется связь. Эта связь может быть искажена шумом (так, едва ли можно ожидать, что по данным из примера с прогнозированием цен акций можно построить абсолютно точный прогноз, поскольку на цену влияют и другие факторы, не представленные во входном наборе данных, и, кроме того, в задаче присутствует элемент случайности), но она должна существовать.
Как правило, нейронная сеть используется тогда, когда неизвестен точный вид связей между входами и выходами, - если бы он был известен, то связь можно было бы моделировать непосредственно.
Другая существенная особенность нейронных сетей состоит в том, что зависимость между входом и выходом находится в процессе обучения сети. Для обучения нейронных сетей применяются алгоритмы двух типов (разные типы сетей используют разные типы обучения): управляемое ("обучение с учителем") и не управляемое ("без учителя"). Чаще всего применяется обучение с учителем, и именно этот метод сейчас рассмотрим.
Для управляемого обучения сети пользователь должен подготовить набор обучающих данных. Эти данные представляют собой примеры входных данных и соответствующих им выходов. Сеть учится устанавливать связь между первыми и вторыми. Обычно обучающие данные берутся из исторических сведений. В рассмотренных выше примерах это могут быть предыдущие значения цен акций и индекса FTSE, сведения о прошлых заемщиках - их анкетные данные и то, успешно ли они выполнили свои обязательства, примеры положений робота и его правильной реакции.
Затем нейронная сеть обучается с помощью того или иного алгоритма управляемого обучения (наиболее известным из них является метод обратного распространения, предложенный в работе Rumelhart et al., 1986), при котором имеющиеся данные используются для корректировки весов и пороговых значений сети таким образом, чтобы минимизировать ошибку прогноза на обучающем множестве. Если сеть обучена хорошо, она приобретает способность моделировать (неизвестную) функцию, связывающую значения входных и выходных переменных, и впоследствии такую сеть можно использовать для прогнозирования в ситуации, когда выходные значения неизвестны.
Сбор данных для нейронной сети
Если задача будет решаться с помощью нейронной сети, то необходимо собрать данные для обучения. Обучающий набор данных представляет собой набор наблюдений, для которых указаны значения входных и выходных переменных. Первый вопрос, который нужно решить, - какие переменные использовать и сколько (и каких) наблюдений собрать.
Выбор переменных (по крайней мере, первоначальный) осуществляется интуитивно. Опыт работы в данной предметной области поможет определить, какие переменные являются важными. При работе с пакетом ST Neural Networks можно произвольно выбирать переменные и отменять предыдущий выбор; кроме того, система ST Neural Networks умеет сама опытным путём отбирать полезные переменные. Для начала имеет смысл включить все переменные, которые могут влиять на результат - на последующих этапах следует сократить это множество.
Нейронные сети могут работать с числовыми данными, лежащими в определённом ограниченном диапазоне. Это создаёт проблемы в случаях, когда данные имеют нестандартный масштаб, когда в них имеются пропущенные значения и когда данные являются нечисловыми. В пакете ST Neural Networks имеются средства, позволяющие справиться со всеми этими трудностями. Числовые данные масштабируются в подходящий для сети диапазон, а пропущенные значения можно заменить на средние значения (или на другую статистику) этой переменной по всем имеющимся обучающим примерам (Bishop, 1995).
Более трудной задачей является работа с данными нечислового характера. Чаще всего нечисловые данные бывают представлены в виде номинальных переменных типа Пол = {Муж, Жен}. Переменные с номинальными значениями можно представить в числовом виде, и в системе ST Neural Networks имеются средства для работы с такими данными. Однако нейронные сети не дают хороших результатов при работе с номинальными переменными, которые могут принимать много разных значений.
Пусть, например, мы хотим научить нейронную сеть оценивать стоимость объектов недвижимости. Цена дома очень сильно зависит от того, в каком районе города он расположен. Город может быть подразделён на несколько десятков районов, имеющих собственные названия, и кажется естественным ввести для обозначения района переменную с номинальными значениями. К сожалению, в этом случае обучить нейронную сеть будет очень трудно, и вместо этого лучше присвоить каждому району определённый рейтинг (основываясь на экспертных оценках).
Нечисловые данные других типов можно либо преобразовать в числовую форму, либо объявить незначащими. Значения дат и времени, если они нужны, можно преобразовать в числовые, вычитая из них начальную дату (время). Обозначения денежных сумм преобразовать совсем несложно. С произвольными текстовыми полями (например, фамилиями людей) работать нельзя, и их нужно сделать незначащими.
Вопрос о том, сколько наблюдений нужно иметь для обучения сети, часто оказывается непростым. Известен ряд эвристических правил, увязывающих число необходимых наблюдений с размерами сети (простейшее из них гласит, что число наблюдений должно быть в десять раз больше числа связей в сети). На самом деле это число зависит также от (заранее неизвестной) сложности того отображения, которое нейронная сеть стремится воспроизвести. С ростом количества переменных количество требуемых наблюдений растёт нелинейно, так что уже при довольно небольшом (например, пятьдесят) числе переменных может потребоваться огромное число наблюдений.
Для большинства реальных задач бывает достаточно нескольких сотен или тысяч наблюдений. Для особо сложных задач может потребоваться еще большее количество, однако очень редко может встретиться (даже тривиальная) задача, где хватило бы менее сотни наблюдений. Если данных меньше, чем здесь сказано, то на самом деле недостаточно информации для обучения сети, и лучшее, что можно сделать - это попробовать подогнать к данным некоторую линейную модель.
В пакете ST Neural Networks реализованы средства для подгонки линейных моделей (см. раздел про линейные сети, а также материал по модулю Множественная регрессия системы STATISTICA).
Во многих реальных задачах приходится иметь дело с не вполне достоверными данными. Значения некоторых переменных могут быть искажены шумом или частично отсутствовать. Пакет ST Neural Networks имеет специальные средства работы с пропущенными значениями (они могут быть заменены на среднее значение этой переменной или на другие её статистики), так что если не так много данных, то можно включить в рассмотрение случаи с пропущенными значениями (хотя, конечно, лучше этого избегать). Кроме того, нейронные сети в целом устойчивы к шумам. Однако у этой устойчивости есть предел. Например, выбросы, т.е. значения, лежащие очень далеко от области нормальных значений некоторой переменной, могут исказить результат обучения. В таких случаях лучше всего постараться обнаружить и удалить эти выбросы (либо удалив соответствующие наблюдения, либо преобразовав выбросы в пропущенные значения). Если выбросы выявить трудно, то можно воспользоваться имеющимися в пакете ST Neural Networks возможностями сделать процесс обучения устойчивым к выбросам (с помощью функции ошибок типа "городских кварталов"; см. Bishop, 1995). Однако такое устойчивое к выбросам обучение, как правило, менее эффективно, чем стандартное.
Следовательно, при работе с НС необходимо выбирать такие переменные, которые, по предположению, влияют на результат.
С числовыми и номинальными переменными в пакете ST Neural Networks можно работать непосредственно. Переменные других типов следует преобразовать в указанные типы или объявить незначащими.
Для анализа нужно иметь порядка сотен или тысяч наблюдений; чем больше в задаче переменных, тем больше нужно иметь наблюдений. Пакет ST Neural Networks имеет средства для распознавания значимых переменных, поэтому следует включать в рассмотрение переменные, в значимости которых нет уверенности.
В случае необходимости можно работать с наблюдениями, содержащими пропущенные значения. Наличие выбросов в данных может создать трудности. Если возможно, следует удалить выбросы. Если данных достаточное количество, следует убрать из рассмотрения наблюдения с пропущенными значениями.
Пре/пост процессирование
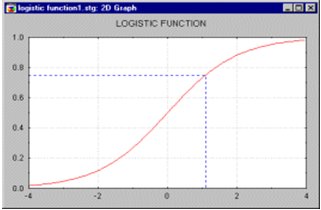
Всякая нейронная сеть принимает на входе числовые значения и выдаёт на выходе также числовые значения. Передаточная функция для каждого элемента сети обычно выбирается таким образом, чтобы её входной аргумент мог принимать произвольные значения, а выходные значения лежали бы в строго ограниченном диапазоне. При этом, хотя входные значения могут быть любыми, возникает эффект насыщения, когда элемент оказывается чувствительным лишь к входным значениям, лежащим в некоторой ограниченной области. На этом рисунке представлена одна из наиболее распространённых передаточных функций - так называемая логистическая функция (рис.11.9) (иногда её также называют сигмоидной функцией, хотя если говорить строго, это всего лишь один из частных случаев сигмоидных - т.е. имеющих форму буквы S - функций). В этом случае выходное значение всегда будет лежать в интервале (0,1), а область чувствительности для входов чуть шире интервала (-1,+1). Данная функция является гладкой, а её производная легко вычисляется - это обстоятельство весьма существенно для работы алгоритма обучения сети (в этом также кроется причина того, что ступенчатая функция для этой цели практически не используется).
Коль скоро выходные значения всегда принадлежат некоторой ограниченной области, а вся информация должна быть представлена в числовом виде, очевидно, что при решении реальных задач методами нейронных сетей требуются этапы предварительной обработки - пре-процессирования - и заключительной обработки - пост-процессирования данных (Bishop, 1995). Соответствующие средства имеются в пакете ST Neural Networks. Здесь нужно рассмотреть два вопроса:
Шкалирование. Числовые значения должны быть приведены в масштаб, подходящий для сети. Обычно исходные данные масштабируются по линейной шкале. В пакете ST Neural Networks реализованы алгоритмы минимакса и среднего/стандартного отклонения, которые автоматически находят масштабирующие параметры для преобразования числовых значений в нужный диапазон.
В некоторых случаях более подходящим может оказаться нелинейное шкалирование (например, если заранее известно, что переменная имеет экспоненциальное распределение, имеет смысл взять ее логарифм). Нелинейное шкалирование не реализовано в модуле ST Neural Networks. Вы можете прошкалировать переменную средствами преобразования даных базовой системы STATISTICA, а затем работать с ней в модуле ST Neural Networks.
Номинальные переменные. Номинальные переменные могут быть двузначными (например, Пол ={Муж, Жен}) или многозначными (т.е. принимать более двух значений или состояний). Двузначную номинальную переменную легко преобразовать в числовую (например, Муж = 0, Жен = 1). С многозначными номинальными переменными дело обстоит сложнее. Их тоже можно представить одним числовым значением (например, Собака = 0, Овца = 1, Кошка = 2), однако при этом возникнет (возможно) ложное упорядочивание значений номинальной переменной: в рассмотренном примере Овца окажется чем-то средним между Собакой и Кошкой. Существует более точный способ, известный как кодирование 1-из-N, в котором одна номинальная переменная представляется несколькими числовыми переменными. Количество числовых переменных равно числу возможных значений номинальной переменной; при этом всякий раз ровно одна из N переменных принимает ненулевое значение (например, Собака = {1,0,0}, Овца = {0,1,0}, Кошка = {0,0,1}). В пакете ST Neural Networks имеются возможности преобразовывать как двух-, так и многозначные номинальные переменные для последующего использования в нейронной сети. К сожалению, номинальная переменная с большим числом возможных состояний потребует при кодировании методом 1-из-N очень большого количества числовых переменных, а это приведёт к росту размеров сети и создаст трудности при её обучении. В таких ситуациях возможно (но не всегда достаточно) смоделировать номинальную переменную с помощью одного числового индекса, однако лучше будет попытаться найти другой способ представления данных.
Задачи прогнозирования можно разбить на два основных класса: классификация и регрессия.
В задачах классификации нужно бывает определить, к какому из нескольких заданных классов принадлежит данный входной набор. Примерами могут служить предоставление кредита (относится ли данное лицо к группе высокого или низкого кредитного риска), диагностика раковых заболеваний (опухоль, чисто), распознавание подписи (поддельная, подлинная). Во всех этих случаях, очевидно, на выходе требуется всего одна номинальная переменная. Чаще всего (как в этих примерах) задачи классификации бывают двузначными, хотя встречаются и задачи с несколькими возможными состояниями.
В задачах регрессии требуется предсказать значение переменной, принимающей (как правило) непрерывные числовые значения: завтрашнюю цену акций, расход топлива в автомобиле, прибыли в следующем году и т.п.. В таких случаях в качестве выходной требуется одна числовая переменная.
Нейронная сеть может решать одновременно несколько задач регрессии и/или классификации, однако обычно в каждый момент решается только одна задача. Таким образом, в большинстве случаев нейронная сеть будет иметь всего одну выходную переменную; в случае задач классификации со многими состояниями для этого может потребоваться несколько выходных элементов (этап пост-процессирования отвечает за преобразование информации из выходных элементов в выходную переменную).
В пакете ST Neural Networks для решения всех этих вопросов реализованы специальные средства пре- и пост-процессирования, которые позволяют привести сырые исходные данные в числовую форму, пригодную для обработки нейронной сетью, и преобразовать выход нейронной сети обратно в формат входных данных. Нейронная сеть служит "прослойкой"между пре- и пост-процессированием, и результат выдаётся в нужном виде (например, в задаче классификации выдается название выходного класса). Кроме того, в пакете ST Neural Networks пользователь может (если пожелает) получить прямой доступ к внутренним параметрам активации сети.