Интеллектуальные задачи в экономике
Оператор скрещивания
На первом этапе скрещивания выбираются пары хромосом из родительской популяции (родительского пула). Это временная популяция, состоящая из хромосом, отобранных в результате селекции и предназначенных для дальнейших преобразований операторами скрещивания и мутации с целью формирования новой популяции потомков. На данном этапе хромосомы из родительской популяции объединяются в пары. Это производится случайным способом в соответствии с вероятностью скрещивания 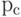 . Далее для каждой пары отобранных таким образом родителей разыгрывается позиция гена (локус) в хромосоме, определяющая так называемую точку скрещивания. Если хромосома каждого из родителей состоит из L генов, то очевидно, что точка скрещивания
. Далее для каждой пары отобранных таким образом родителей разыгрывается позиция гена (локус) в хромосоме, определяющая так называемую точку скрещивания. Если хромосома каждого из родителей состоит из L генов, то очевидно, что точка скрещивания 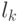 представляет собой натуральное число, меньшее L. Поэтому фиксация точки скрещивания сводится к случайному выбору числа из интервала
представляет собой натуральное число, меньшее L. Поэтому фиксация точки скрещивания сводится к случайному выбору числа из интервала ![[1, L - 1].](/sites/default/files/tex_cache/b05fda883e1c82ce073c8ad9d754193c.png) В результате скрещивания пары родительских хромосом получается следующая пара потомков:
В результате скрещивания пары родительских хромосом получается следующая пара потомков:
- потомок, хромосома которого на позициях от 1 до
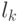 состоит из генов первого родителя, а на позициях от
состоит из генов первого родителя, а на позициях от  до
до  - из генов второго родителя;
- из генов второго родителя; - потомок, хромосома которого на позициях от 1 до
 состоит из генов второго родителя, а на позициях от
состоит из генов второго родителя, а на позициях от 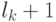 до
до  - из генов первого родителя.
- из генов первого родителя.
Оператор мутации с вероятностью рт изменяет значение гена в хромосоме на любое другое возможное значение. Например, если в хромосоме [100110101010] мутации подвергается ген на позиции 7, то его значение, равное 1, изменяется на 0. что приводит к образованию хромосомы [100110001010]. Как уже упоминалось выше, вероятность мутации обычно очень мала, и именно от нее зависит, будет данный ген мутировать или нет. Вероятность рт мутации может эмулироваться, например, случайным выбором числа из интервала [0, 1] для каждого гена и отбором для выполнения этой операции тех генов, для которых разыгранное число оказывается меньшим или равным значению рт.
Формирование новой популяции. Хромосомы, полученные в результате применения генетических операторов к хромосомам временной родительской популяции, включаются в состав новой популяции. Она становится так называемой текущей популяцией для данной итерации генетического алгоритма. На каждой очередной итерации рассчитываются значения функции приспособленности для всех хромосом этой популяции, после чего проверяется условие остановки алгоритма и либо фиксируется результат в виде хромосомы с наибольшим значением функции приспособленности, либо осуществляется переход к следующему шагу генетического алгоритма, т.е. к селекции. В классическом генетическом алгоритме вся предшествующая популяция хромосом замещается новой популяцией потомков, имеющей ту же численность.
Выбор "наилучшей" хромосомы. Если условие остановки алгоритма выполнено, то следует вывести результат работы, т.е. представить искомое решение задачи. Лучшим решением считается хромосома с наибольшим значением функции приспособленности.
В завершение следует признать, что генетические алгоритмы унаследовали свойства естественного эволюционного процесса, состоящие в генетических изменениях популяций организмов с течением времени.
Главный фактор эволюции - это естественный отбор (т.е. природная селекция), который приводит к тому, что среди генетически различающихся особей одной и той же популяции выживают и оставляют потомство только наиболее приспособленные к окружающей среде.
Рассмотрим алгоритм решения следующей задачи: необходимо оптимизировать эффективность от вложения средств в различные проекты, операции, недвижимость и т.д. Эффективность будет определяться как доходность от вложенных средств, в зависимости от того, в какой период они распределены. Рассмотрим возможность организации размещения средств в N периодах (что соответствует краткосрочному, среднесрочному и долгосрочному периодам, соответственно). Допустим, у организации есть альтернатива из М вариантов вложения средств в разные проекты в различные периоды. Вектор 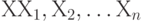 , где
, где 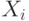 - вариант вложения средств в i-м периоде.
- вариант вложения средств в i-м периоде.
В данном случае вектор X будет являться хромосомой (индивидуумом), состоящей из набора N генов.
Необходимо найти глобальный максимум функции F(Х), определяющей доходность данного размещения средств в рассматриваемых периодах.
В результате работы алгоритма получим выходной вектор X, являющийся наилучшим вариантом плана вложения средств на N ближайших периодов.
Проведение двух серий экспериментов приводит к следующим выводам:
- независимо от того, каково первое поколение, результирующий ген будет одним и тем же;
- количество итераций работы алгоритма невозможно предугадать;
- чем больше размер поколения, тем меньшее количество итераций необходимо сделать, однако при этом увеличивается время обработки поколения;
- большая вероятность мутации уменьшает количество итераций для достижения максимального значения, однако стабильность поколений при этом резко уменьшается;
- количество генов, выбираемых для порождения нового поколения, зависит от размера популяции.
Определены следующие преимущества генетических алгоритмов:
- не требуется никакой информации о поверхности ответов;
- разрывы, существующие на поверхности ответа, имеют незначительное влияние на эффективность алгоритма.
В литературе обосновывается невысокая эффективность традиционных методик применительно к решению сложных практических задач. Именно к такой категории можно отнести монополистическую конкуренцию с её большим объёмом исходной информации, одновременным наличием количественно и качественно определённых параметров, а также требованиями к оперативности их обработки. В связи с этим в работе предлагается применить генетический алгоритм, как инструмент быстрого поиска решения.
Однако при всей эффективности генетического алгоритма он представляет собой лишь общее описание процесса, протекающего в биологических системах.
Инициализация, то есть формирование исходной популяции, заключается в случайном выборе заданного количества хромосом (особей), представляемых двоичными последовательностями фиксированной длины. В условиях конкуренции такой подход к формированию не вполне применим.
Во-первых, поведение всех участников рыночного процесса не хаотично, а является результатом глубокого анализа ситуации и поведения других субъектов. В связи с этим вполне закономерным является рассмотрение в качестве хромосомы вектора характеристик товара, а, соответственно, в качестве исходной популяции - совокупности векторов характеристик всех участников данного рынка.
Такое преобразование целесообразно при незначительной длине хромосомы. В условиях монополистической конкуренции на рынке представлено большое количество дифференцированного товара. Причём для достижения этих различий отдельные продукты могут иметь весьма малые отличия, и для их фиксации может потребоваться существенное число характеристик. Следовательно, длина вектора характеристик товара не является малой. Кроме того, важно учесть, что этот вектор состоит из ценовых и неценовых параметров. Однако применять алгоритм к неоднородным хромосомам нельзя. Поэтому предлагается выполнить нормализацию значений отдельно в рамках каждой из групп ценовых и неценовых характеристик.
В-третьих, необходимо уточнить природу популяции. В условиях совершенной конкуренции каждый отдельный производитель или потребитель не оказывали влияния на процесс формирования цены и других параметров товара. Они действовали абсолютно независимо. В условиях монополии наоборот одно предприятие, безусловно, доминирует. Рынок монополистической конкуренции отличается наличием на нем достаточно большого числа независимых монополистов, производящих (или потребляющих) различный товар и способных в определенной степени воздействовать на параметры товара своих конкурентов. В связи с этим предлагаем формировать популяцию на основе характеристик товара только производителей или только потребителей, в зависимости от варианта рассмотрения конкуренции.
Следующим важнейшим этапом является оценка приспособленности хромосом в популяции. Оно основано в расчете функции приспособленности для каждой хромосомы этой популяции. Чем больше значение этой функции, тем выше "качество" хромосомы. Функция приспособленности является очень важным понятием в генетических алгоритмах и иначе называется функцией оценки. Она представляет меру приспособленности данной особи в популяции и позволяет оценить её качество в соответствии с эволюционным принципом выживания "сильнейших" (лучше всего приспособившихся).
Форма функции приспособленности зависит от характера решаемой задачи. В большинстве случаев функция принимает неотрицательные значения, а также для решения оптимизационной задачи её требуется максимизировать. Однако в реальных условиях может требоваться не только её максимизация или минимизация, но одновременное применение обоих подходов при реализации алгоритма, как, например, при рассмотрении совершенной конкуренции.
Применительно к монополистической конкуренции, значение функции приспособленности должно рассчитываться на основе величин ценовых и неценовых характеристик. В силу того, что суть получения конкурентного преимущества состоит в предложении рынку товара с опережающими параметрами, для решения оптимизационной задачи предлагается применить максимизацию этой функции. Однако, в отличие от совершенной конкуренции, где соперничество происходило с учётом пожеланий и производителей, и потребителей (в силу отсутствия влияния на рынок), в условиях монополистического рынка в конкурентном взаимодействии принимает участие только одна сторона (только производители или только потребители). Это является одним из следствий возможности воздействия на рынок.
Определение возможности остановки генетического алгоритма также зависит от конкретных условий. Если известно максимальное (или минимальное) значение функции приспособленности, остановка может произойти после получения ожидаемого оптимального значения или после достижения заданной точности. Другой причиной остановки является отсутствие улучшения решения задачи. Кроме того, алгоритм может быть остановлен по истечении определённого времени выполнения либо после выполнения заданного количества итераций. Если условие остановки выполнено, то производится переход к выбору "наилучшей" хромосомы. В противном случае на следующем шаге выполняется селекция. Все перечисленные события могут являться причиной остановки генетического алгоритма при решении задачи конкуренции. Выбор варианта остановки следует рассматривать отдельно применительно к ценовой и неценовой конкуренции.
Селекция хромосом также осуществляется по значениям функции приспособленности и состоит в выборе хромосом, которые будут участвовать в создании потомков для следующей популяции (нового поколения). Существуют различные методы селекции. Наиболее популярным считается так называемый "метод рулетки", который свое название получил по аналогии с известной азартной игрой. Каждой хромосоме может быть сопоставлен сектор колеса рулетки, величина которого устанавливается пропорциональной значению функции приспособленности данной хромосомы. Поэтому, чем больше значение функции приспособленности, тем больше сектор на колесе рулетки. Всё колесо рулетки соответствует сумме значений функции приспособленности, всех хромосом популяции. В силу того, что одним из событий генетического процесса является мутация, такой случайный подход является вполне применимым. Селекция хромосомы может быть представлена как результат поворота колеса рулетки, поскольку "выигравшая" хромосома относится к выпавшему сектору этого колеса. Очевидно, что чем больше сектор, тем больше вероятность "победы" соответствующей хромосомы. Поэтому вероятность выбора данной хромосомы оказывается пропорциональной значению её функции приспособленности.
В результате процесса селекции создается родительский пул, равный по численности текущей популяции, но разделённой по парам. В том случае, если исходная популяция содержала нечётное количество хромосом, предлагается оставшуюся хромосому перенести в новую популяцию потомков без выполнения скрещивания. Таким образом, понижается риск потери значимой генетической информации. Кроме того, предлагается перенести операцию выбора (естественный отбор) наиболее "качественных" хромосом на этап формирования новой популяции. Благодаря этому на первой итерации работы алгоритма будут учтены векторы характеристик всех товаров. Применение генетических операторов к хромосомам приводит к формированию новой популяции потомков.
Важно отметить, что оператор мутации играет второстепенную роль по сравнению с оператором скрещивания. Это означает, что скрещивание в алгоритме производится всегда, тогда как мутация - достаточно редко, по аналогии с миром живых организмов. В генетическом алгоритме мутация хромосом может выполняться на популяции родителей перед скрещиванием либо на популяции потомков, образованных в результате скрещивания. Кроме того, многие из описанных выше процессов протекают случайным образом, что вполне может быть рассмотрено, как реализация оператора мутации. Таким образом, применительно к монополистической конкуренции, отдельно мутация рассматриваться не будет.
К объединённым в пары хромосомам родительского пула применяется оператор скрещивания (crossover). Далее для каждой пары родителей разыгрывается позиция гена (локус), определяющая точку скрещивания. Если хромосома каждого из родителей состоит из L генов, то точка скрещивания z представляет собой натуральное число, меньшее L. Фиксация точки скрещивания сводится к случайному выбору числа из интервала [1, L-1]. В результате скрещивания пары родительских хромосом получается следующая пара потомков:
- Потомок, хромосома которого на позициях от 1 до z состоит из генов первого родителя, а на позициях от
 до
до  - из генов второго родителя.
- из генов второго родителя. - Потомок, хромосома которого на позициях от 1 до z состоит из генов второго родителя, а на позициях от
 до
до  - из генов первого родителя.
- из генов первого родителя.
Такой вариант скрещивания называют одноточечным. Также применяются и другие виды скрещивания.
Возрастание числа точек скрещивания существенно усложняет алгоритм, но ведет к увеличению точности результата. Положительный эффект объясняется тем, что при большом числе точек степень "слияния" (взаимного проникновения) хромосом возрастает. Следовательно, полученные потомки лучшим образом отражают исходные характеристики родительских хромосом. В природе число точек разрыва выбирается случайно для любой из родительских пар. Очевидно, что реализация такого же механизма в случае конкурентного взаимодействия будет оказывать положительный эффект и приближать модель к реальному процессу. В связи с этим, предлагается следующая процедура:
- выполнить генерацию случайного числа точек разрыва J из диапазона [1, L-1], где L - число генов в хромосоме;
- выполнить J генераций точек скрещивания
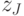 ;
; - указанная процедура выполняется для каждой пары родительского пула.
Следующим важным этапом генетического алгоритма является формирование новой популяции. Хромосомы, полученные в результате применения генетических операторов к хромосомам временной родительской популяции, включаются в состав новой популяции. Она становится новым поколением для данной итерации генетического алгоритма. На каждой очередной итерации рассчитываются значения функции приспособленности для всех хромосом этой популяции, реализуется выбор (естественный отбор) хромосом, после чего проверяется условие остановки алгоритма и либо фиксируется результат в виде хромосомы с наибольшим значением функции приспособленности, либо осуществляется переход к следующему шагу генетического алгоритма, то есть к селекции.
Этот выбор выполняется по принципу естественного отбора - наибольшие шансы в создании новых особей имеют хромосомы с наибольшими значениями приспособленности. Принцип естественного отбора имеет однозначную трактовку для биологических систем. Однако применительно к другим задачам его можно трактовать, как выбор наиболее характерных представителей того или иного класса. Так при рассмотрении совершенной конкуренции наиболее характерными представителями популяции производителей были хромосомы с наибольшими значениями приспособленности. Поэтому процесс селекции строился на основе исключения хромосом с минимальной приспособленностью как наименее характерных. Для популяции потребителей процесс был обратным. В условиях монополистической конкуренции получение конкурентных преимуществ возможно путем предложения рынку товаров с опережающими конкурентов параметрами. В связи с этим следует реализовывать механизм отбора хромосом с наибольшими значениями приспособленности, для чего на каждой итерации предлагается исключать одну хромосому с наименьшей функцией приспособленности.
В классическом генетическом алгоритме вся предшествующая популяция хромосом замещается новой популяцией потомков, имеющей ту же численность. Благодаря предложенной процедуре отбора на каждой итерации численность популяции нового поколения сокращается. Поэтому, ситуацию, когда в ней останется две хромосомы можно рассматривать, как естественную точку останова алгоритма. Лучшим решением считается хромосома с наибольшим значением функции приспособленности. Эта хромосома представляет искомое решение задачи, то есть вектор характеристик наиболее конкурентоспособного товара.
Предложенная адаптация базовых шагов генетического алгоритма позволяет сделать вывод о принципиальной возможности его применения к условиям конкуренции. Однако основная особенность монополистического рынка, то есть требование одновременного учёта ценовых и неценовых характеристик товара, не позволяют предложить универсальный алгоритм. Это связано с различной природой этих параметров товара.
С точки зрения конкурентных преимуществ большей конкурентоспособностью обладает товар с опережающими неценовыми характеристиками, так как именно они отражают качество товара с позиции его потребительской ценности. Следовательно, максимизация функции приспособленности позволит двигаться в направлении улучшения неценовых параметров. Применительно к ценовым характеристикам конкурентоспособность выражается в максимизации только тех параметров, увеличение значения которых повышает потребительскую ценность товара. Среди этого множества есть характеристики, возрастание которых, наоборот, негативно влияет на ценность товара. Примером такой характеристики является цена товара. Данное обстоятельство должно быть учтено при формировании модели именно ценовой конкуренции монополистического рынка.
