Программирование

3.5 Функции

В Octave файлы с расширением .m могут содержать не только тексты программ (группа операторов и функций Octave), но и могут быть оформлены как отдельные функции. В этом случае имя функции должно совпадать с именем файла, в котором она хранится (например, функция с именем primer должна храниться в файле primer.m).

Функция в Octave имеет следующую структуру.

Первая строка функции это заголовок:

function

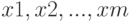Здесь — имя функции, — список входных параметров функции, 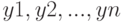— список выходных параметров функции. Функция заканчивается служебным словом 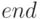. Таким образом, в простейшем случае структуру функции можно записать следующим образом:

	
function [ y1, y2, . . ., yn]= name_function ( x1, x2, . . .,xm)
	оператор 1;
	оператор 2;
	. . .
	операторk;
end

В файле с расширением .m, кроме основной функции, имя которой совпадает с именем файла, могут находиться так называемые подфункции. Эти функции доступны только внутри файла.

Таким образом, общую структуру функции можно представить так:

	
% Здесь начинается основная функция m-файла, имя которой должно
% совпадать с именем файла, в котором она хранится
function[y1, y2, . . ., yn]= name_function(x1, x2, . . .,xm)
% Среди операторов основной функции могут быть операторы
% вызова подфункций f1, f2, f3, . . .,fl
	оператор 1;
	оператор 2;
	. . .
	операторk;
end; % здесь заканчивается основная функция
function[y1, y2, . . ., yn]= f1(x1, x2, . . .,xm) % начало первой подфукции
	операторы
end % конец первой подфункции
function[y1, y2, . . ., yn]= f2(x1, x2, . . .,xm) % начало второй подфукции
	операторы
end % конец второй подфункции
. . .
function[y1, y2, . . ., yn]= fn(x1, x2, . . .,xm) % начало n-й подфукции
	операторы
end % конец n-й подфункции

Такая структура, близка к структуре программ на языке Си. Она не допускает вложенности функций друг в друга. Однако в Octave возможен и другой синтаксис, в котором разрешено использование вложенных функций, поэтому структура основной функции может быть и такой:

	
function[y1, y2, . . ., yn]= name_function(x1, x2, . . .,xm)
	function[y1, y2, . . ., yn]= f1(x1, x2, . . .,xm)% начало первой подфукции
		операторы
	end % конец первой подфункции
	function[y1, y2, . . ., yn]= f2(x1, x2, . . .,xm)% начало второй подфукции
		операторы
	end % конец второй подфункции
	. . .
	function[y1, y2, . . ., yn]= fn(x1, x2, . . .,xm) % начало n-й подфукции
		операторы
	end % конец n-й подфункции
	оператор1;
	оператор2;
	. . .
	операторk;
end % здесь заканчивается основная функция

Рассмотрим пример.

Пример 3.17. Написать функцию, предназначенную для удаления из массива 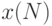простых чисел.

Функцию назовём 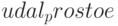. Её входными данными являются: числовой массив 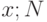— количество элементов в массиве. Выходными данными функции 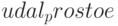будут: массив , из которого удалены простые числа; новый размер массива после удаления из него простых чисел.

В функции 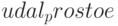будут использоваться две вспомогательные функции: функция , которая проверяет, является ли число простым; функция 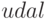удаления элемента из массива.

Заголовок основной функции имеет вид:

Заголовок подфункции запишем так:

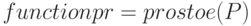
Функция prostoe проверяет, является ли число 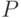простым, она возвращает 1, если 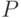— простое, 0 — в противном случае.

Заголовок подфункции 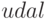имеет вид:

Функция 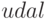удаляет из массива 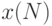элемент с номером 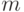, функция возвращает модифицированный массив и изменённое значение .

В листинге 3.21 приведено содержимое файла udal_prostoe.m с комментариями.

	
% Функция udal_prostoe удаляет из массива x(N) простые числа и возвращает
% модифицированный массив x и изменённое значение N в качестве результата.
function[x N]= udal_prostoe(x, N)
	i =1;
	while i<=N
			L=prostoe(x(i)); % Проверяем является ли число x(i) простым.
			if L==1 % если число простое (L=1),
				[x N]= udal(x, i,N); % то удаляем из массива i-ый элемент,
			else % иначе переходим к следующему элементу массива.
				i=i +1;
			end;
	end;
end % Окончание основной функции udal_prostoe.
% Функция prostoe проверяет является ли число P простым,
% она возвращает 1, если P — простое, 0 — если число P не является простым.
function pr=prostoe(P)
pr=1
for i =2:P/2
	if mod(P, i)==0
		pr =0;
		break;
	end
end
end % Окончание функции prostoe.
% Функция udal удаляет из массива x элемент с номером m.
function [ x N]= udal ( x,m,N)
% Удаление происходит путём смещения элементов, начиная с m-го на одну
% позицию влево. Выходными элементами функции будут массив x, из которого
% удалён один элемент и уменьшенное на 1 количество (N) элементов в массиве.
for i=m: N-1
	x(i)=x(i+1);
end
x(:,N) = [ ]; % После смещения элементов удаляем последний элемент и
N=N-1; % уменьшаем количество элементов в массиве на 1.
end % Окончание функции udal.

В листинге 3.21 был использован синтаксис не допускающий вложенность функций друг в друга. Листинг 3.22 содержит текст программы, структура которой допускает вложенность функций.

	
function[x N]= udal_prostoe1(x, N)
	function pr=prostoe(P)
		pr =1;
		for i =2:P/2
			if mod(P, i)==0
					pr =0;
					break;
			end
		end
	end
	function[x N]= udal(x,m,N)
			for i=m: N-1
					x(i)=x(i +1);
			end
			x(:,N) = [ ];
			N=N-1;
	end
	i =1;
	while i<=N
			L=prostoe(x(i));
			if L==1
				[x N]= udal(x, i,N);
			else
				i=i +1;
			end;
	end;
end

Нижне представлено обращение к функции для удаления простых чисел из массива z(8).

	
>>> z =[4 6 8 7 100 13 88 1 2 5];
>>> [y k]= udal_prostoe(z, 8);
y = 4 6 8 100 88 125
k= 6

Аналогичным образом можно составлять и более сложные функции, в состав которых входит множество вспомогательных функций.

В Octave есть возможность передавать имя функции как входной параметр, что существенно расширяет возможности программирования. Вообще говоря, имя функции передаётся как строка, а её вычисление осуществляется с помощью функции feval.

Функция предоставляет альтернативный способ вычисления значения функции.

Параметрами функции являются: строка с именем вызываемой функции, в качестве имени может быть встроенная функция или определённая пользователем функция; параметры этой функции, разделённые запятой.

В качестве параметра можно передать строку с именем функции, а затем с помощью функции обратиться к передаваемой функции. следующей задачи.

Пример 3.18. Вычислить значение функций и в точке .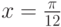

Вычисление можно осуществить обычным способом или с использованием функции :

	
>>> x=pi /12
x = 0.26180
>>> sin(pi /12)
ans = 0.25882
>>> feval(’sin’, x)
ans = 0.25882
>>> cos(pi/12)
ans = 0.96593
>>> feval(’cos’, x)
ans = 0.96593

Как известно, многие функции Octave допускают обращение к ним с различным числом параметров. При этом алгоритм функций анализирует количество входных параметров и осуществляет корректную работу при различном количестве входных параметров.

Рассмотрим, как создавать функции, в которых может использоваться разное количество входных параметров. В качестве входного параметра в этом случае будет использоваться массив ячеек, который позволяет хранить разнородные данные, то есть все входные параметры хранятся в виде единственного параметра массива ячеек varargin. С помощью функции length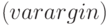 можно вычислить количество поступивших в функцию входных параметров, а с помощью конструкции — обратиться к -му входному параметру.

Рассмотрим простой пример функции с переменным числом параметров.

Пример 3.19. Найти сумму всех входных параметров функции.

Будем считать, что все входные параметры — скалярные величины.

Выходными параметрами функции будут найденная сумма 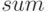и строка , в которой будет храниться аварийное сообщение, если строка не найдена.

В листинге 3.24 приведена программа решения задачи с комментариями.

	
% Функция вычисления суммы входных параметров, хранящихся в массиве.
% Функция возвращает значение суммы в переменной sum, а в переменной
% s формируется сообщение об ошибке, если невозможно найти сумму
% (если среди входных параметров были нечисловые значения).
function[sum s]=sum_var(varargin)
% числами.
	pr =1; % pr = 1, если все элементы массива ячеек являются числами.
	Sum=0; % До начала суммирования в переменную Sum запишем 0.
% length(varavgin) возвращает количество входных параметров sum_var
	for i =1: length(varargin) % цикл по i для перебора всех входных
							% параметров от 1 до length(varargin).
			if isnumeric(varargin{ i })==1 % проверяем, является ли
										% i-ый входной параметр числом,
					Sum=Sum+varargin{ i }; % да — добавляем varargini к Sum.
			else % если не является,
					pr =0; % записываем в pr = 0,
					Sum=0; % обнуляем сумму Sum
					break; % и прерываем цикл.
			end;
	end
	if pr==1 % Если pr=1, то все входные параметры были числами
				% и сумма их найдена
			s = [ ]; % очищаем переменную s, аварийного сообщения нет.
	else % иначе записываем в s аварийное сообщение.
			s=’Во входных параметрах были нечисловые данные’
	end
end
% Вызов функции
>>> Summa=sum_var(1, 2, 3, 4, 5)
Summa = 15
>>> Summa=sum_var(pi, 1.23, e)
Summa = 7.0899

Под рекурсией в программировании понимается вызов функции из её тела. Классическими рекурсивными алгоритмами являются возведение числа в целую положительную степень, вычисление факториала и т.д. В рекурсивных алгоритмах функция вызывает саму себя до выполнения какого-либо условия. Рассмотрим пример.

Пример 3.20. Вычислить -е число Фибоначчи.

Если нулевой элемент последовательности равен нулю, первый — единице, а каждый последующий представляет собой сумму двух предыдущих, то это последовательность Фибоначчи (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, . . . ).

Текст функции (листинг 3.25):

	
function F=fibonachi(N)
	if(N==0) | (N==1)
		F=N;
	else
		F=fibonachi(N-1)+fibonachi(N-2);
	end
end
% Вызов функции
>>> fibonachi(2)
ans = 1
>>> fibonachi(0)
ans = 0
>>> fibonachi(6)
ans = 8