Основы Maxima
2.8 Решение задач элементарной математики
2.8.1 Нахождение корней уравнений и систем алгебраических уравнений
Решение алгебраических уравнений и их систем осуществляется при помощи функции 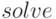 , в качестве параметров. В первых квадратных скобках указывается список уравнений через запятую, во вторых — список переменных, через запятую (либо несколько упрощённые формы записи):
, в качестве параметров. В первых квадратных скобках указывается список уравнений через запятую, во вторых — список переменных, через запятую (либо несколько упрощённые формы записи):
-
 — решение одного уравнения относительно переменной
— решение одного уравнения относительно переменной  ;
; -
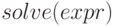 — решение уравнения с одной неизвестной и числовыми коэффициентами;
— решение уравнения с одной неизвестной и числовыми коэффициентами; -
![solve([eqn_1,... ,eqn_n], [x_1,... ,x_n])](/sites/default/files/tex_cache/da44e15909c2a6b650f6c2a289d5b4e3.png) — решение системы уравнений.
— решение системы уравнений.
Примеры:
Решение одного уравнения с одним неизвестным
(%i7) solve(x^2-5*x+4);
![[x=1,x=4]\leqno{(\%o7) }](/sites/default/files/tex_cache/07caa1ae56182e4e9bd13aae04e18eb4.png)
Решение одного уравнения в символьном виде:
(%i2) solve([x-a/x+b], [x]);
![[x=-\frac{\sqrt{{b}^{2}+4\,a}+b}{2},x=\frac{\sqrt{{b}^{2}+4\,a}-b}{2}]\leqno{(\%o2) }](/sites/default/files/tex_cache/e56defb642d806d3b82bb0ec31c24bcb.png)
Решение системы уравнений в символьном виде:
(%i10) solve([x*y/(x+y)=a,x*z/(x+z)=b,y*z/(y+z)=c], [x,y,z]);
![\begin{math}
(\%o10) [[x=0,y=0,z=0],
[x=\frac{2abc}{\left( b+a\right) c-ab}, y=\frac{2abc}{\left( b-a\right) c+ab},
z=-\frac{2abc}{\left( b-a\right) c-ab}]]
\end{math}](/sites/default/files/tex_cache/9a73883802c5bd028e2bc4d58fe8c851.png)
В последнем примере решений несколько, и Maxima выдаёт результат в виде списка.
Функция 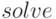 применима и для решения тригонометрических уравнений. При этом в случае множества решений у тригонометрических уравнений выдаётся соответствующее сообщение только и одно из решений.
применима и для решения тригонометрических уравнений. При этом в случае множества решений у тригонометрических уравнений выдаётся соответствующее сообщение только и одно из решений.
Пример:
(%i13) solve([sin(x)=0], [x]); solve: using arc-trig functions to get a solution. Some solutions will be lost.
![[x=0]\leqno{(\%o13) }](/sites/default/files/tex_cache/f21dfd6ecdfddfb34ddfa4dcb9ce16b0.png)
Также Maxima позволяет находить комплексные корни
(%i18) solve([x^2+x+1], [x]);
![[x=-\frac{\sqrt{3}\,i+1}{2},x=\frac{\sqrt{3}\,i-1}{2}]\leqno{(\%o18) }](/sites/default/files/tex_cache/81bdb1cb8e41d799e78511ad5b1f2686.png)
2.9 Построение графиков и поверхностей
Для вывода графиков на экран или на печать при помощи Maxima существуют несколько вариантов форматов и, соответственно, программ вывода графики, а именно:
-
 (Tcl/Tk программа с графическим интерфейсом пользователя; элемент xMaxima)
(Tcl/Tk программа с графическим интерфейсом пользователя; элемент xMaxima) -
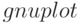 (мощная утилита для построения графиков, обмен с Maxima — через канал)
(мощная утилита для построения графиков, обмен с Maxima — через канал) -
 (Tk-интерфейс к
(Tk-интерфейс к  с рудиментарным графическим интерфейсом пользователя; включён в дистрибутив Maxima)
с рудиментарным графическим интерфейсом пользователя; включён в дистрибутив Maxima) -
 (встроенные возможности
(встроенные возможности  -а к Maxima)
-а к Maxima)
Все варианты интерфейса (кроме wxMaxima) для построения графиков используют две базовых функции: 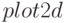 (построение двумерных графиков) и
(построение двумерных графиков) и 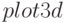 (построение трехмерных графиков).
(построение трехмерных графиков).
При использовании wxMaxima кроме них используются ещё две аналогичные команды: 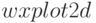 и
и 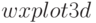 . Все команды позволяют либо вывести график на экран, либо (в зависимости от параметров функции) в файл.
. Все команды позволяют либо вывести график на экран, либо (в зависимости от параметров функции) в файл.
2.9.1 Построение графика явной функции y = f(x)
График функции 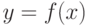 на отрезке
на отрезке ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) можно построить с помощью функции
можно построить с помощью функции ![plot2d(f(x), [x,a,b], опции](/sites/default/files/tex_cache/3b1ced57b38f6a72d6413177b1f55074.png) ) или
) или ![plot2d(f(x), [x,a,b], [y,c,d], опции](/sites/default/files/tex_cache/0bdeea50e610009664994a8c0e1dceee.png) ). Опции не обязательны, однако, для изменения свойств графика их нужно задавать. Параметр
). Опции не обязательны, однако, для изменения свойств графика их нужно задавать. Параметр ![[y,c,d]](/sites/default/files/tex_cache/a3ae239d770bdb93c0dc7346fd29e45c.png) можно не задавать, тогда высота графика выбирается по умолчанию. Построим график функции
можно не задавать, тогда высота графика выбирается по умолчанию. Построим график функции  на отрезке
на отрезке ![[-4\pi, 4\pi]](/sites/default/files/tex_cache/1fc65feb0147e6058a4da606148da3d6.png) .
.
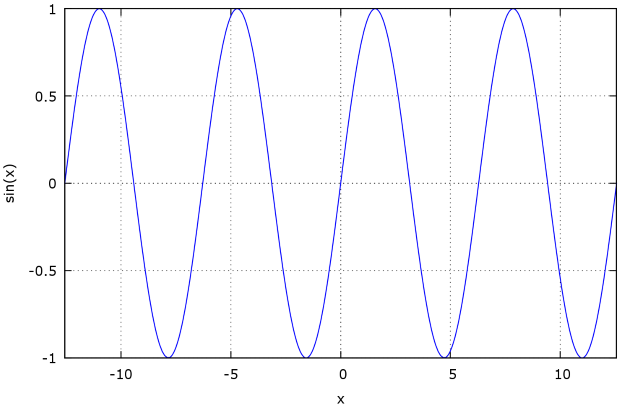
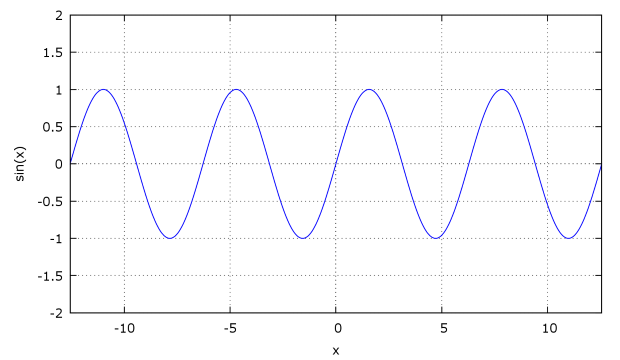
(%i2) plot2d(sin(x), [x, -4*%pi, 4*%pi]); (%i3) plot2d(sin(x), [x, -4*%pi, 4*%pi],[y,-2,2]);
Результаты приведены на рис. 2.1, рис. 2.2
2.9.2 Построение графиков функций, заданных параметрически
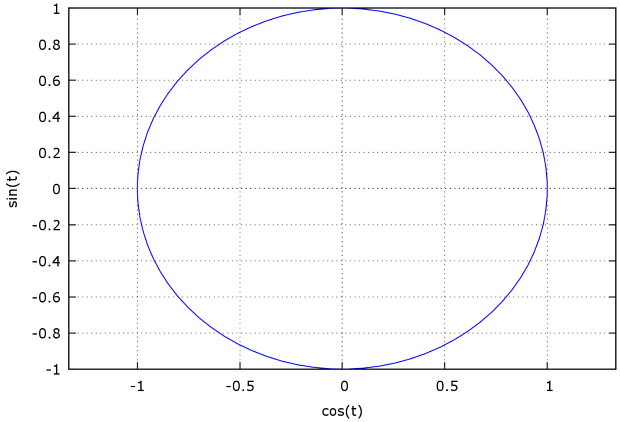
Для построения графиков функций, заданных параметрически, используется опция  . Для построения графика указывается область изменения параметра. Пример графика простейшей параметрической функции представлен на рис. 2.3.
. Для построения графика указывается область изменения параметра. Пример графика простейшей параметрической функции представлен на рис. 2.3.
Команда построения графика: plot2d ([parametric, cos(t), sin(t), [t,-%pi,%pi], [nticks,80]],[x, -4/3, 4/3])
увеличить изображение
Рис. 2.2. Простейшая команда построения графика с указанием интервала по оси Oy
увеличить изображение
Рис. 2.3. Простейшая команда построения графика функции, заданной параметрически
Опция 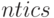 указывает число точек, по которым проводится кривая.
указывает число точек, по которым проводится кривая.
Рассмотрим некоторые опции.
Опции указываются в виде аргументов функции 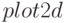 в квадратных скобках. Возможна установка легенды, меток на осях, цвета и стиля графика. Применение нескольких опций характеризует следующий пример:
в квадратных скобках. Возможна установка легенды, меток на осях, цвета и стиля графика. Применение нескольких опций характеризует следующий пример:
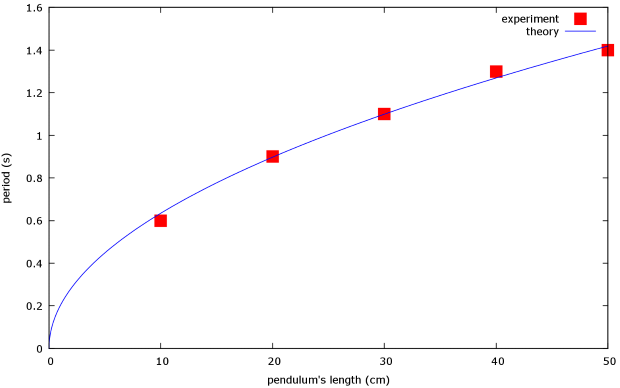
(%i17) plot2d([[discrete,xy], 2*%pi*sqrt(l/980)], [l,0,50], [style, [points,5,2,6], [lines,1,1]], [legend, experiment , theory ], [xlabel,"pendulum's length (cm)"], [ylabel,"period (s)"]);
В данном примере в одних осях строятся два графика. Первый ![([discrete,xy])](/sites/default/files/tex_cache/5b0bcfc0fa2c1b80431889d907eef7c3.png) строится в виде точек по массиву
строится в виде точек по массиву 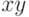 с указанием стиля
с указанием стиля  . Второй строится по уравнению функции
. Второй строится по уравнению функции 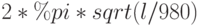 с указанием стиля
с указанием стиля  . Опция
. Опция  указывает подписи кривых, опции
указывает подписи кривых, опции 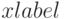 и
и 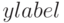 — подписи осей. Результат приведён на рис. 2.4.
— подписи осей. Результат приведён на рис. 2.4.
Формирование массивов для построения графика осуществляется следующим образом:
(%i12) xx:[10, 20, 30, 40, 50]; (%i13) yy:[.6, .9, 1.1, 1.3, 1.4]; (%i14) xy:[[10,.6], [20,.9], [30,1.1], [40,1.3], [50,1.4]];
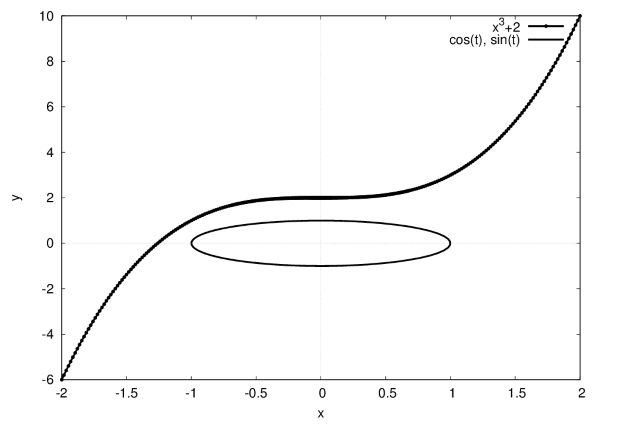
Можно комбинировать в одних осях графики кривых различного типа: функции 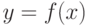 или параметрические
или параметрические
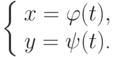
например (см.рис. 2.5):
plot2d ([x^3+2, [parametric, cos(t), sin(t), [t, -5, 5], [nticks,80]]], [x, -2, 2], [xlabel, "x"],[ylabel, "y"], [style, [linespoints,3,2], [lines,3,1]], [gnuplot_term, ps], [gnuplot_out_file, "test.eps"]);
Опции [gnuplot_term, ps], [gnuplot_out_file, "test.eps"] указывают, что графическая иллюстрация выводится в файл 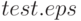 в формате
в формате 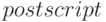 (бэкенд для вывода графиков —
(бэкенд для вывода графиков — 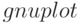 ).
).
Опции [style,[linespoints,3,2],lines,3,1]] позволяют указать стиль линий на графике (линия с точками или сплошная линия).
Для вывода результатов в формат  можно использовать опции (указание размеров 400,400 в общем случае необязательно): [gnuplot_term, png size 400,400],[gnuplot_out_file, max.png]
можно использовать опции (указание размеров 400,400 в общем случае необязательно): [gnuplot_term, png size 400,400],[gnuplot_out_file, max.png]
2.9.3 Построение кривых в полярной системе координат
Для построения графика в полярных координатах нужно задать изменение значений полярного радиуса и полярного угла. Пусть 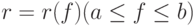 — зависимость полярного радиуса
— зависимость полярного радиуса  от полярного угла
от полярного угла  . Тогда график этой функции в полярных координатах можно построить, задав у функции
. Тогда график этой функции в полярных координатах можно построить, задав у функции 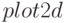 опцию [gnuplot_preamble, set polar; set zeroaxis ]. Данная опция будет действовать лишь при условии, что выбран формат графика
опцию [gnuplot_preamble, set polar; set zeroaxis ]. Данная опция будет действовать лишь при условии, что выбран формат графика 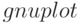 .
.
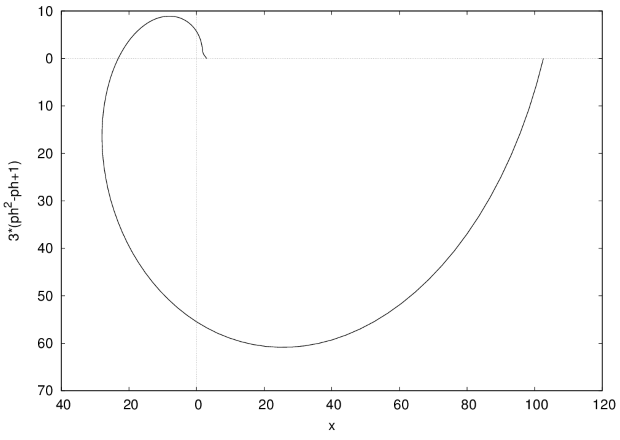
Пример: построить в полярных координатах график функции 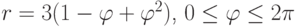 .
.
Для создания графика используем команду:
plot2d([3*(1-ph+ph^2)],[ph,0,2*%pi],[gnuplot_preamble,"set polar", "set zeroaxis","set encoding koi8r"],[xlabel,x],[gnuplot_term,ps], [gnuplot_out_file, "max.eps"],[plot_format,gnuplot]);
Результат приведён на рис. 2.6. Толщину и стиль линии можно регулировать, используя опцию 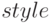 (например, опция [style, [lines,3,1]] устанавливает ширину линии 3 и синий цвет).
(например, опция [style, [lines,3,1]] устанавливает ширину линии 3 и синий цвет).
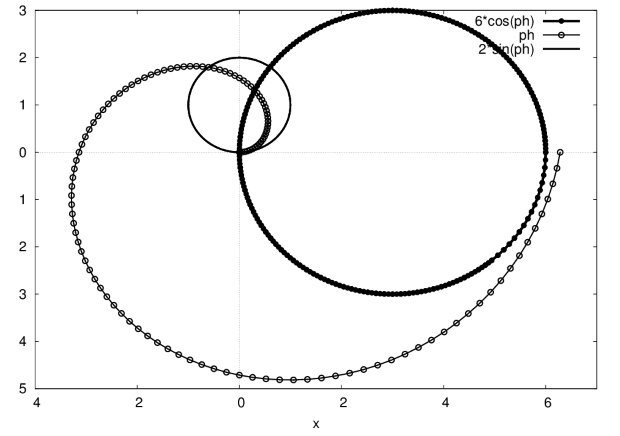
Пример: построить в полярных координатах графики трёх функций  .
.
Для создания графика используем команду:
plot2d([6*cos(ph),ph,2*sin(ph)],[ph,0,2*%pi],[gnuplot_preamble, "set polar","set zeroaxis","set encoding koi8r"],[xlabel, x], [gnuplot_term,ps],[gnuplot_out_file, "max3.eps"], [plot_format,gnuplot]);
Результат приведён на рис. 2.7.
2.9.4 Построение трёхмерных графиков
Основная команда для построения трёхмерных графиков — 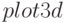 . Рассмотрим технологию построения графиков с использованием интерфейса
. Рассмотрим технологию построения графиков с использованием интерфейса 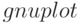 . Поверхность функции в цветном изображении строится с использованием опции
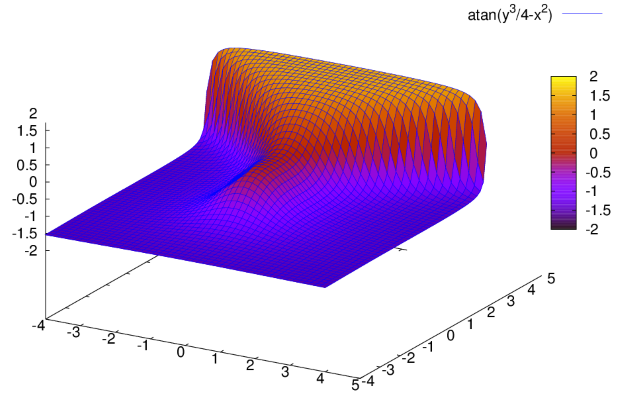
. Поверхность функции в цветном изображении строится с использованием опции  (рис. 2.8).
(рис. 2.8).
Пример:
(%i2) plot3d (atan (-x^2 + y^3/4), [x, -4, 4], [y, -4, 4], [grid, 50, 50], [gnuplot_pm3d,true],[gnuplot_term,ps], [gnuplot_out_file,"plot31.eps"]);
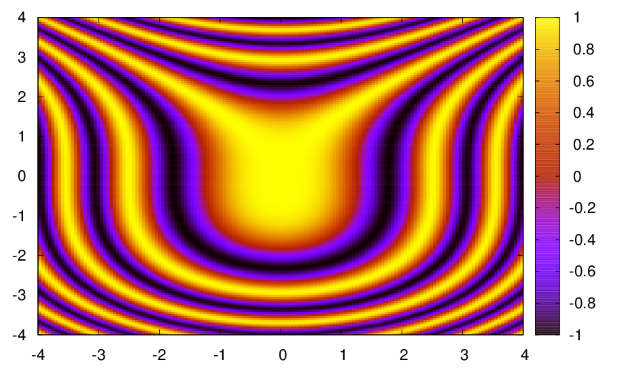
С использованием этой опции и особенностей программы  можно построить и изображение линий уровня функции. Пример (рис. 2.9 ):
можно построить и изображение линий уровня функции. Пример (рис. 2.9 ):
(%i3) plot3d (cos (-x^2 + y^3/4), [x, -4, 4], [y, -4, 4], [gnuplot_preamble,"set view map"], [gnuplot_pm3d, true], [grid, 150, 150],[gnuplot_term,ps], [gnuplot_out_file,"plot32.eps"]);
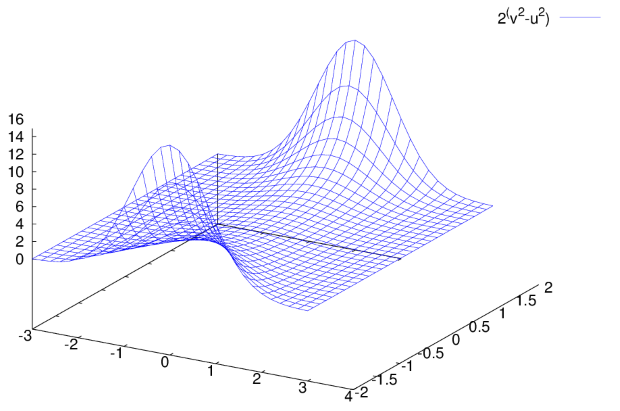
Более строгий результат можно получить, используя стандартный формат функции 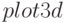 . Пример (рис. 2.10):
. Пример (рис. 2.10):
(%i4) plot3d (2^(-u^2 + v^2), [u, -3, 3], [v, -2, 2]);
Для вывода графика в файл всё равно необходимо использовать опции  (установить терминал
(установить терминал  и имя файла результата). Необходимая команда:
и имя файла результата). Необходимая команда:
(%i5) plot3d (2^(-u^2 + v^2), [u, -3, 3], [v, -2, 2], [gnuplot_term,ps],[gnuplot_out_file,"plot33.eps"]);
Смена формата графики также возможна за счёт использования опций 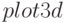 . Пример (вывод графики в формате
. Пример (вывод графики в формате  —
рис. 2.11):
—
рис. 2.11):
(%i6) plot3d (2^(-u^2 + v^2), [u, -3, 3], [v, -2, 2], [plot_format, openmath]);
Достоинством данного формата является встроенная возможность сохранения копии графического изображения в файл, редактирования и поворота построенного графика.
Функция, для которой строится трёхмерный график, может задаваться как Maxima или Lisp-функция, лямбда-функция либо выражение Maxima общего вида. При использовании формата 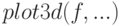 выражение
выражение  рассматривается как функция двух переменных. При использовании формата
рассматривается как функция двух переменных. При использовании формата ![plot3d([f_1,f_2,f_3],...)](/sites/default/files/tex_cache/231d6256424a05ee89ab6430685ccd00.png) , каждая функция
, каждая функция 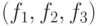 рассматривается как функция трёх переменных.
рассматривается как функция трёх переменных.
Пример использования формата ![plot3d([f_1,f_2,f_3],...)](/sites/default/files/tex_cache/231d6256424a05ee89ab6430685ccd00.png) (рис. 2.12):
(рис. 2.12):
Функция 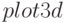 позволяет строить графики функций, заданных в цилиндрических или сферических координатах за счёт использования преобразования координат (опция [transform_xy, polar_to_xy] или функция make_transform (vars, fx, fy, fz)).
позволяет строить графики функций, заданных в цилиндрических или сферических координатах за счёт использования преобразования координат (опция [transform_xy, polar_to_xy] или функция make_transform (vars, fx, fy, fz)).
Определённые преимущества обеспечивает формат 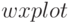 , имеющийся в графическом интерфейсе wxMaxima (
, имеющийся в графическом интерфейсе wxMaxima (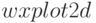 и
и 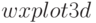 ). Команда построения графика в формате wxMaxima по синтаксису мало отличается от синтаксиса команд
). Команда построения графика в формате wxMaxima по синтаксису мало отличается от синтаксиса команд 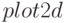 и
и 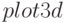 . Качество воспроизведения графиков на экране wxMaxima относительно невысокое, но легко, выделив график щелчком мыши, сохранить его в файл (по умолчанию
. Качество воспроизведения графиков на экране wxMaxima относительно невысокое, но легко, выделив график щелчком мыши, сохранить его в файл (по умолчанию 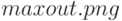 ). Качество копии в файле намного лучше, чем рисунка в окне wxMaxima.
). Качество копии в файле намного лучше, чем рисунка в окне wxMaxima.

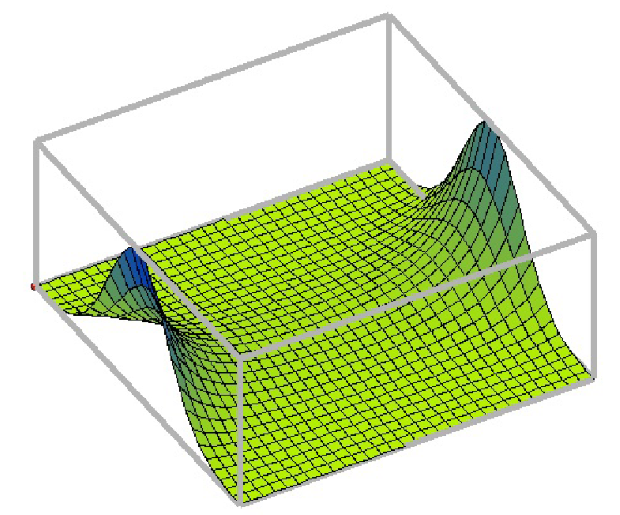
![График функции, определённой в формате [f1,f2,f3]](/EDI/13_11_16_1/1478989280-19722/tutorial/704/objects/2/files/2.12.png)