Системотехнические аспекты перспективных компьютерных технологий
7.3. Базовые модели квантовых компьютеров
В квантовых компьютерах ( КК ) основная ставка делается на предельный и недостижимый в субмикронной электронике режим распараллеливания вычислений на физико-техническом уровне их организации. Авторы идеи использования квантовых процессов при вычислениях [177, 178] исходили из того, что состояние квантовой системы из 
двухуровневых элементов (кубитов) можно описать некоторой когерентной суперпозицией из 
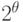булевых состояний, так как в отличие от классических физических систем состояние квантовой системы описывается вектором состояния в 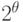-мерном гильбертовом пространстве. Это автоматически приводит к тому, что в КК коэффициент распараллеливания вычислений только на
физическом уровне равен 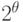. Однако для использования таких потенциальных возможностей КК необходимо [94, 193]:
- Выделить и зафиксировать в пространстве в кубитов (синтезировать "рабочее тело" КК ) и с помощью избирательных воздействий перевести его в конечное состояние , которое отвечает результату выполненного алгоритма.
- Обеспечить циклическую инициализацию или установку входного -кубитного регистра в исходное основное базисное состояние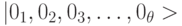
. Здесь
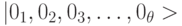- -мерный вектор состояния по Дираку, представляемый матрицей-столбцом в 0-мерном гильбертовом пространстве. - Обеспечить помехоустойчивость выполняемых преобразований и по максимуму подавить декогерентизацию квантовых состояний, которая обусловлена взаимодействиями квантового "рабочего тела" с внешней средой, в том числе и паразитными.
- Выбрать квантовое "рабочее тело" таким образом, чтобы между составляющими его кубитами имели место только определенные нелинейные взаимодействия, обеспечивающие выполнение одно- и двухкубитовых операций (купирование только функционально значимых нелинейных взаимодействий между кубитами).
- Обеспечить надежное измерение (идентификацию) конечного состояния квантового "рабочего тела".
При переходе в квантовую область сохраняются основные положения классической теории передачи, хранения и преобразования информации Винера - Шеннона [14, 15] с той разницей, что в КК энтропия служит мерой неопределенности измерения (идентификации) фактического состояния квантовой системы, которое характеризуется волновой функцией Шредингера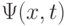 
, если квантовая система полностью изолирована от окружающей среды (замкнута). Здесь 
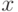- полный набор всех непрерывных и дискретных переменных, характеризующих состояние квантовой системы, которыми, в частности, могут быть координаты и спиновые моменты всех частиц, составляющих систему. Такие состояния принято называть чистыми (когерентными) [94], и в КК каждый составляющий кубит может находиться в одном из двух таких состояний: 
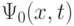или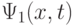 
, первое из которых условно считается "нулевым", а второе - "единичным".
Для описания чистых состояний квантовой системы можно использовать вектор состояния Дирака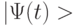 
, который представляет собой матрицу-столбец в гильбертовом пространстве и имеет размерность, равную числу чистых состояний квантовой системы (в случае кубита вектор состояния Дирака имеет размерность 2).
Любое взаимодействие квантовой системы с внешней средой (в том числе и через входные и выходные интерфейсы КК ) приводит к флуктуа-циям ее макроскопических характеристик, необратимым процессам диссипации энергии в ней и, как следствие, к разрушению квантовой когерентности, именуемой декогерентизацией [94]. При достижении квантовой системы термодинамического равновесия с внешней средой ее состояние считается смешанным (некогерентным) и описывается не волновой функцией, а положительно определенным оператором (матрицей) плотности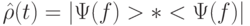 
который является результатом усреднения аналогичного оператора замкнутой системы по неконтролируемым состояниям внешней среды, которые в совокупности образуют более "общую" замкнутую систему Здесь 
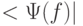- эрмитово-сопряженный вектор состояния системы.
Сохранение когерентности суперпозиции состояний кубитов составляет центральную физико-техническую проблему создания реальных КК. При этом требуется, чтобы время декогерентизации было больше, чем время реализации алгоритма, то есть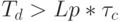 
. Как показывает опыт МКМД-бит-потоковых вычислительных технологий, для реализации слов- и поток-инструкций требуется 
бит-инструкций, откуда следует, что время декогерентизации должно превосходить время выполнения основных квантовых операций на четыре и более порядков.
Центральная системотехническая проблема создания КК состоит в том, что для описания поведения -кубитного регистра требуется задать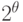 
комплексных чисел, что практически исключает возможность моделирования когерентных суперпозиций на основе традиционных ЭВМ уже при 
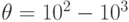. Объясняется это тем, что размерность пространства состояний квантового "рабочего тела" из 
кубитов составляет величины порядка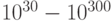 
. Отсюда следует, что схемотехническое моделирование квантового "рабочего тела" из сотен и более кубитов практически невозможно с использованием традиционных инструментальных ЭВМ. Для этого требуются компьютеры на основе квантовых логических вентилей, работа которых описывается в 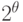- мерном гильбертовом пространстве, то есть инструментальная ЭВМ также должна быть квантовой и фактически идентичной создаваемой.
Перспективы использования КК в основном связывают [94] с решением так называемых NP- полных задач, где на основе квантовых вычислений можно достичь экспоненциального ускорения. Такие задачи принято считать не вычисляемыми на классических компьютерах из-за того, что в них время решения полиномиально зависит от размерности задачи . К классу NP- полных относятся задачи, для которых трудно найти решение, но очень просто его проверить. Отсюда следует, что программно-аппаратные инструментальные платформы для КК удобнее строить на базе нейрокомпьютерных технологий, где в процессе обучения материнской нейро-ЭВМ можно использовать методы проб и ошибок, основанные на направленном или случайном переборе возможных вариантов решения поставленной задачи.
В идеале центральную физико-техническую проблему декогеренти-зации КК можно решить[94, 194, 195] на основе логически и термодинамически обратимых вентилей, в которых энергия, затраченная на переключение из одного когерентного состояния в другое, рассеивается только за счет необратимых периферийных процессов ввода информации в КК и считывания (идентификации) результата на его выходе.
В теории информации в качестве термодинамического предела для энергии переключения классического вентиля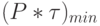 
принято считать предельное значение работы 
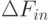, которую необходимо выполнить для того, чтобы перевести вентиль в состояние, отличное от исходного. Поэтому на 1 бит информационной энтропии [94] необходимо затратить 
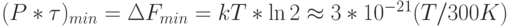Дж/бит, где 
Дж*К-1 - постоянная Больцмана, 
- мощность, расходуемая в процессе переключения, а 
- время переключения вентиля. Однако в этом случае высока вероятность ложного срабатывания вентиля за счет тепловых флуктуаций 
, то есть такие энергетические затраты приводят к максимальной неопределенности при оценке текущего состояния вентиля. Поэтому в качестве классического термодинамического предела для энергии переключения выбрана величина с более чем 6-кратным запасом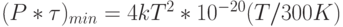 
Дж/бит, которой соответствует 
.
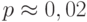В этом случае при увеличении количества информации внутри системы на 1 бит ее внутренняя энергия должна увеличиться на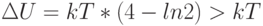 
, что приводит к ее накоплению в квантовой системе пропорционально росту числа вентилей, частоте и продолжительности их работы.
Отсюда встает задача преодоления квазиклассического термодинамического барьера и построения термодинамически и логически обратимого КК. Из приведенных соотношений видно, что стирание 1 бита информации увеличивает энтропию квантовой системы на величину 
, что приводит к рассеянию энергии и выделению тепла 
. В результате логически необратимая операция одновременно является и термодинамически необратимой [94]. Это говорит о том, что вентили реальных КК можно сделать только логически обратимыми, а их термодинамическую обратимость можно считать только условной и ее можно выдерживаться только при определенных условиях и на ограниченных интервалах времени. Для этого можно использовать адиабатическую динамическую логику [94, 196], в рамках которой частота переключательных процессов настолько мала, что обеспечивается релаксация всех составляющих вентилей в квазиравновесное состояние. Это позволяет считать вычислительный процесс адиабатическим, в котором энергия
не рассеивается, а минимальная работа переключения практически полностью расходуется на изменение внутренней энергии квантового "рабочего тела" 
, которую можно возвратить для полезного использования в последующих циклах его "возбуждения". Однако и в этом случае не удается полностью исключить диссипацию энергии [94, 197], что не является обязательным условием сохранения логической необратимости.
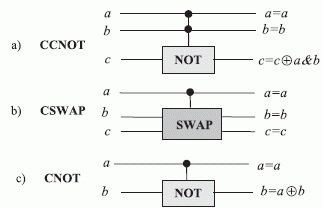
Компромиссное решение состоит в том, чтобы логически обратимым считать тот вентиль, в котором по сигналам на выходе можно однозначно восстановить значение сигналов на его входах. Такие логически, но не термодинамически обратимые вентили были предложены в рамках консервативной логики [94, 198], основу которой образуют (рис. 7.5) вентили дважды контролируемого "НЕ" ( CCNOT ) и контролируемого обмена ( SWAP ).
Эти вентили имеют по три входа и выхода, обладают базисным свойством в том смысле, что на их основе можно представить любую логическую функцию от большего числа переменных, а логически обратимый характер выполняемых ими преобразований задается правилами табл. 7.1. По аналогичной схеме можно выполнить и "ИСКЛЮЧАЮЩЕЕ ИЛИ" ( CNOT ), которое базисным свойством не обладает, но широко используется в вычислительной технике (см. рис. 7.5-с).
В основу квантовых вентилей (кубитов) можно положить достаточно широкий спектр реальных квантовых процессов [94]:
- захват ионов, лежащих на низкоэнергетических уровнях, ионными ловушками, сформированными в вакууме с помощью электромагнитных полей определенной конфигурации, с лазерным охлаждением самих ионов до микрокельвиновских температур;
- преобразования ядерных полуцелых спинов и эффекты ядерного магнитного резонанса (ЯМР);
- преобразования макроскопических квантовых состояний сверхпроводящих устройств;
- взаимодействия двух спиновых или двух орбитальных электронных состояний в квантовых точках;
- квантовые эффекты в электродинамических полостях и фотонных кристаллах и т. д.
| а | b | с | CCNOT | CSWAP | ||||
|---|---|---|---|---|---|---|---|---|
| а | b | с | а | b | с | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
Несмотря на такое разнообразие квантовых процессов, используемых в реальных и реалистичных КК, уже сейчас можно выделить достаточно узкий класс математических моделей (преобразований), описывающих эти процессы. Основное внимание уделяется двум типам квантовых операторов и соответствующих им квантовых вентилей (излагается по [94]). К первым относят различные операторы, которые выполняют одно-кубитовые повороты вектора состояния кубита в двухмерном гильбертовом пространстве:
-
оператор Паули, в соответствии с которым работают вентили типа NOT, выполняющие операции поворота спина
:
( 7.6) -
оператор Адамара
, который выполняет совпадающую с обратной (самообратимую) операцию формирования суперпозиции состояний: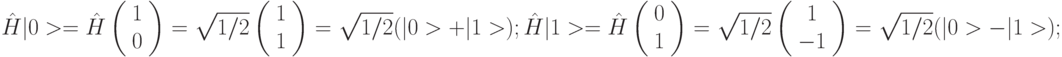
что соответствует
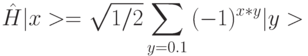
и описывается матрицей
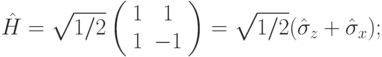
( 7.7)
Суперпозиция двузначных (булевых) состояний в регистре из 
кубитов описывается оператором Уолша - Адамара, который представляет собой прямое произведение однокубитовых операторов Адамара: 
и для него
 |
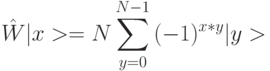( 7.8) |
Где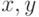 
- цепочки из состояний -кубитов, а 
- побитное скалярное произведение этих цепочек по модулю 2:
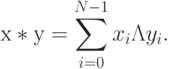
Двухкубитовые операторы и соответствующие им квантовые вентили выполняют повороты в гильбертовом пространстве двух кубитов, взаимодействие между которыми невозможно представить прямым произведением однокубитовых поворотов. Основным вентилем этого типа является CNOT рис. 7.5-с, который совместно с однокубтовыми операторами образует операционный базис для всех унитарных операций, выполняемых квантовой системой из более двух кубитов, и который можно представить матрицей 4*4:
В этом двухкубитовом вентиле кубит 
является контролирующим и описывается симметричной матрицей, так как его схема симметрична относительно входов-выходов. Квантовый вентиль 
является контролируемым и выполняет контролируемую инверсию ( 
) при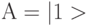 
, то есть, как и в МКМД-бит-потоковых вычислительных технологиях, операция 
используется как условная инверсия. Этот же вентиль можно использовать для копирования или неразрушающего измерения состояния контролирующего кубита , так как при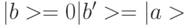 
.
Физический смысл преобразований, выполняемых квантовым вентилем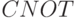 
, проще всего установить из эквивалентной схемы
где составляющие преобразования выполняются слева направо,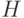 
- однокубитовый вентиль Адамара, а
двухкубитовый оператор контролируемого (избирательного) изменения фазы, который в данном случае осуществляет сдвиг фазы нал и только состояния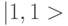 
: 
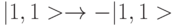, оставляя неизменными остальные состояния кубита.
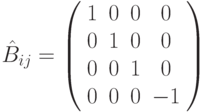
Тип двухкубитного квантового вентиля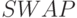 
выполняет обмен состояниями между составляющими кубитами, и его можно представить:
Таким образом, базовые квантовые вентили:
- реализуют операторы не над булевыми переменными, а над их суперпозицией;
- осуществляют либо фазовые сдвиги, либо обмен состояниями с использованием условной инверсии ( );
- выполняют преобразования над потоками данных и по специализированным для каждого оператора схемам соединения составляющих вентилей.
Существующие экспериментальные КК реализуют уже ряд квантовых алгоритмов и обладают всеми признаками традиционных компьютеров: загружают информацию, обрабатывают ее и выдают результаты. Но они еще обладают малой оперативной памятью (единицы и десятки кубит) и низким быстродействием. Так, операция выборки из четырех элементов осуществляется на двух кубитах за десятки миллисекунд, что пока не позволяет им конкурировать с классическими компьютерами.
Один из первых экспериментальных КК ориентирован на реализацию алгоритма Дойча - Джозса [94, 199], который используется при решении следующей задачи.