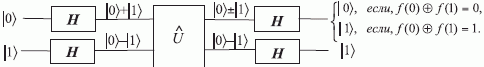Системотехнические аспекты перспективных компьютерных технологий
Имеется набор из четырех булевых функций одной переменной: 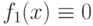 ;
; 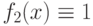 ;
; 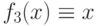 и
и  , из которых первые две принадлежат классу "константных" функций, а две последние - классу "сбалансированных". Требуется определить, к какому классу относится произвольная булева функция
, из которых первые две принадлежат классу "константных" функций, а две последние - классу "сбалансированных". Требуется определить, к какому классу относится произвольная булева функция 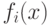 .
.
В классическом компьютере для ее решения необходимо вычислить  и
и 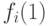 , то есть подать два входных операнда ("0" и "1") и выполнить над ними две операции. В КК Дойча - Джозса на решение той же задачи требуется всего одна, но более "сложная" операция. Ориентированный на решение этой задачи КК состоит из двух кубитов [94], первый из которых находится в состоянии
, то есть подать два входных операнда ("0" и "1") и выполнить над ними две операции. В КК Дойча - Джозса на решение той же задачи требуется всего одна, но более "сложная" операция. Ориентированный на решение этой задачи КК состоит из двух кубитов [94], первый из которых находится в состоянии 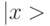 и реализует функции входного интерфейса, а второй - в состоянии
и реализует функции входного интерфейса, а второй - в состоянии 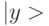 и используется как рабочий. Такой двухкуби-товый КК выполняет унитарную операцию
и используется как рабочий. Такой двухкуби-товый КК выполняет унитарную операцию 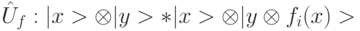 , которую можно представить четырьмя матрицами 4*4, соответствующими четырем возможным функциям
, которую можно представить четырьмя матрицами 4*4, соответствующими четырем возможным функциям  :
:
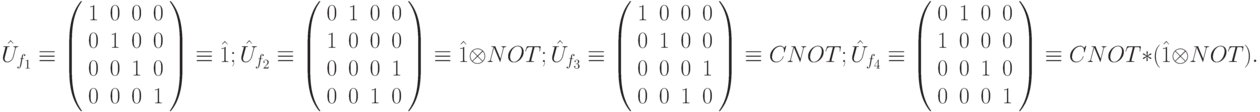
Отвечающая этому оператору квантовая схема имеет вид:
Алгоритмически ориентированный КК Дойча - Джозса работает следующим образом [94, 199]:
- С помощью оператора Адамара сформировать суперпозицию начальных состояний входного и рабочего кубитов, которая при
 имеет вид:
имеет вид: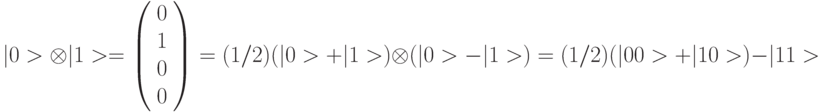
и в которой отдельные составляющие имеют одинаковую амплитуду, но их фазы могут отличаться на
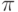 .
. - Выполнить над суперпозицией начальных состояний преобразование:
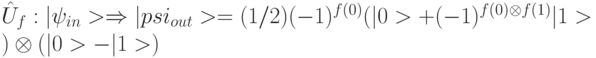 .
.Оно переводит двухкубитный КК в конечное состояние, зависящее от значения относительной фазы
 суперпозиции двух начальных состояний. Здесь использованы следующие эквивалентные преобразования:
суперпозиции двух начальных состояний. Здесь использованы следующие эквивалентные преобразования: 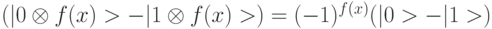 и
и  .
. - С помощью оператора Адамара обратить суперпозицию конечных состояний кубитов и перевести их в начальное состояние. В результате интерфейсный кубит перейдет в состояние
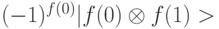 , а рабочий кубит вернется в исходное состояние
, а рабочий кубит вернется в исходное состояние 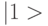 .
.
Таким образом, структурно-функциональная схема алгоритмически ориентированного КК Дойча - Джозса (без учета нормировочных множителей 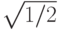 в операторе Адамара (7.7)) имеет вид:
в операторе Адамара (7.7)) имеет вид:
где принадлежность 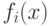 к классу "константных" или "сбалансированных" булевых функций одной переменной определяется не по отдельным значениям
к классу "константных" или "сбалансированных" булевых функций одной переменной определяется не по отдельным значениям 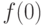 и
и 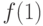 , а по их суперпозиции
, а по их суперпозиции  , задающей фазу результирующего состояния интерфейсного кубита.
, задающей фазу результирующего состояния интерфейсного кубита.
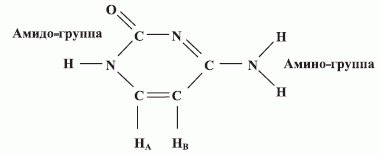
Алгоритмически ориентированный КК Дойча - Джозса был реализован [94, 200] с помощью кубитов на ядерных спинах протонов молекулы цитозина в 50 мМ растворе D2O. Цитозин является компонентой ДНК и имеет два изолированных протона 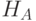 и
и 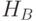 :
:
Это правило вытекает из структуры спектра ядерного магнитного резонанса такой квантовой системы при 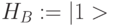 :
:
где поглощению сигнала соответствуют положительные линии спектра 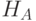 , а излучению сигнала - отрицательные линии
, а излучению сигнала - отрицательные линии 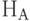 .
.
На основе такой же двухспиновой системы показана возможность построения алгоритмически ориентированного КК Гровера [94, 201, 202]. Такой КК предназначен для поиска объекта 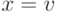 в неупорядоченной базе данных, которая содержит
в неупорядоченной базе данных, которая содержит  объектов
объектов 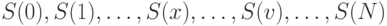 , закодированных
, закодированных 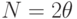 состояниями квантового регистра из
состояниями квантового регистра из  кубитов. Известно условие поиска
кубитов. Известно условие поиска 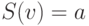 . В обычной ЭВМ на проверку этого условия необходимо израсходовать в худшем случае N операций сравнения (полный перебор базы данных), а при равновероятной гипотезе размещения искомого объекта в базе данных на это уходит в "среднем"
. В обычной ЭВМ на проверку этого условия необходимо израсходовать в худшем случае N операций сравнения (полный перебор базы данных), а при равновероятной гипотезе размещения искомого объекта в базе данных на это уходит в "среднем" 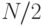 операций сравнения. Быстрый квантовый алгоритм Гровера [94, 203] по оценке ее автора способен решить эту задачу за
операций сравнения. Быстрый квантовый алгоритм Гровера [94, 203] по оценке ее автора способен решить эту задачу за 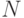 шагов, и для его реализации требуется три типа элементарных унитарных операций.
шагов, и для его реализации требуется три типа элементарных унитарных операций.
Первая унитарная операция представляет собой  -мерное преобразование Уолша - Адамара (7.8). Оно переводит квантовый регистр из
-мерное преобразование Уолша - Адамара (7.8). Оно переводит квантовый регистр из  кубитов в исходное состояние
кубитов в исходное состояние  , которому отвечает суперпозиция
, которому отвечает суперпозиция
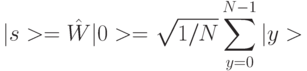
булевых состояний 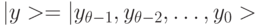 с равными амплитудами
с равными амплитудами 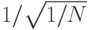 для всех суперпонируемых состояний, включая и искомое
для всех суперпонируемых состояний, включая и искомое 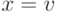 .
.
Вторая унитарная операция также является 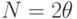 -мерным преобразованием Уолша-Адамара, которое переводит квантовый регистр из произвольного начального состояния
-мерным преобразованием Уолша-Адамара, которое переводит квантовый регистр из произвольного начального состояния  , кодируемого цепочкой
, кодируемого цепочкой 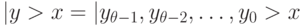 c "нулевыми" (
c "нулевыми" ( 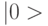 ) и "единичными" (
) и "единичными" ( 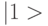 ) состояниями кубитов, в результирующее состояние
) состояниями кубитов, в результирующее состояние 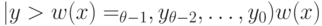 .
.
Знак амплитуды результирующего состояния квантового регистра определяется четностью (parity) побитного скалярного произведения начального и конечного состояний:
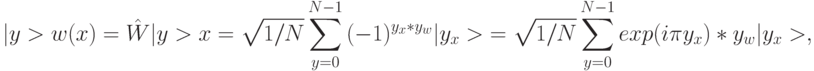
где  .
.
Третья унитарная операция является оператором инверсии (относительно состояния 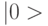 )
)  , который сохраняет вектор состояния
, который сохраняет вектор состояния 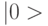 , но изменяет знак всех векторов состояний, ортогональных
, но изменяет знак всех векторов состояний, ортогональных 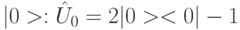 .
.
В общем случае оператор инверсии представляет собой оператор диффузии, который действует на произвольный вектор состояния, сохраняя известный вектор  и изменяя знак у всех векторов в гильбертовой гиперплоскости, ортогональной
и изменяя знак у всех векторов в гильбертовой гиперплоскости, ортогональной 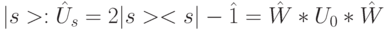 . Это оператор инвертирует знаки всех амплитуд произвольного состояния квантового регистра
. Это оператор инвертирует знаки всех амплитуд произвольного состояния квантового регистра  относительно всех амплитуд известного начального состояния
относительно всех амплитуд известного начального состояния  по правилу
по правилу 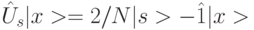 , где
, где  и
и 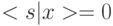 при
при 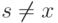 .
.
В алгоритме Гровера итеративно используется оператор 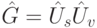 . В нем оператор
. В нем оператор 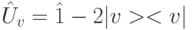 инвертирует амплитуды только состояния
инвертирует амплитуды только состояния 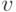 , кодирующего искомый объект. Оператор диффузии
, кодирующего искомый объект. Оператор диффузии 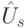 действует на все состояния, кроме искомого, амплитуда которого стала отрицательной после действия оператора
действует на все состояния, кроме искомого, амплитуда которого стала отрицательной после действия оператора 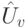 .
.
В результате итеративного выполнения 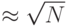 раз оператора
раз оператора  амплитуды всех
амплитуды всех 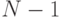 состояний, кроме искомого, сохранят свое начальное значение
состояний, кроме искомого, сохранят свое начальное значение 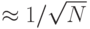 , а отрицательная амплитуда искомого состояния должна возрасти до величины, достаточной для ее идентификации на выходе КК, так как после каждой итерации она увеличивается на величину
, а отрицательная амплитуда искомого состояния должна возрасти до величины, достаточной для ее идентификации на выходе КК, так как после каждой итерации она увеличивается на величину 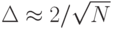 .
.
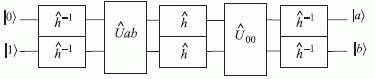
Алгоритмически ориентированный КК Гровера был апробирован [94, 201, 202] на таком же двухкубитовом физико-техническом субстрате, что и КК Дойча - Джозса, но при поиске объекта в базе данных малой размерности  . В таких условиях требуется выполнить только одну итерацию оператора Гровера, который для двухкубитовой квантовой системы имеет вид
. В таких условиях требуется выполнить только одну итерацию оператора Гровера, который для двухкубитовой квантовой системы имеет вид  , где
, где 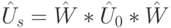 - оператор диффузии,
- оператор диффузии,  , a
, a 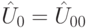 - двухкубитовый оператор инверсии амплитуд всех состояний, кроме состояния
- двухкубитовый оператор инверсии амплитуд всех состояний, кроме состояния  . Схема КК Гровера в этом случае имеет вид:
. Схема КК Гровера в этом случае имеет вид:
и в ней использован модифицированный оператор Адамара
\hat{h}, вращающий фазу не на 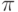 , а на
, а на  .
.
Идентификация результирующего состояния двухкубитового КК Гровера выполняется после одной итерации по правилу, определяемому структурой спектральных линий:
Исследователи математических основ КК на начальном этапе стремились доказать преимущества квантовых алгоритмов перед классическими, чему способствовал успех алгоритмов Гровера и Шора, породивших иллюзию, что КК выполняет анализ функции  переменных за
переменных за  шагов. Однако специалисты Массачусетского технологического института показали [204], что КК способен определить четность функции за
шагов. Однако специалисты Массачусетского технологического института показали [204], что КК способен определить четность функции за 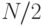 шагов, а алгоритм Гровера является всего лишь частным случаем этой задачи, которая формулируется так: имеется некоторая функция
шагов, а алгоритм Гровера является всего лишь частным случаем этой задачи, которая формулируется так: имеется некоторая функция 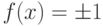 для
для 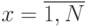 ; требуется определить
; требуется определить  равно
равно 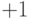 или
или 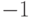 .
.
Классический компьютер решает эту задачу на потоке за  шагов, то есть алгоритмическое ускорение КК составляет всего лишь 2 раза, а не
шагов, то есть алгоритмическое ускорение КК составляет всего лишь 2 раза, а не  раз. Объясняется это тем, что алгоритм Гровера имеет дело с функциями
раз. Объясняется это тем, что алгоритм Гровера имеет дело с функциями  , которые принимают противоположные значения только на одном
, которые принимают противоположные значения только на одном 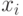 . В результате сейчас идет более объективный анализ преимуществ КК перед классическими, что уже привело к постановкам задач (Ю. Ожигов [205]), где КК проигрывают классическим.
. В результате сейчас идет более объективный анализ преимуществ КК перед классическими, что уже привело к постановкам задач (Ю. Ожигов [205]), где КК проигрывают классическим.
С этих позиций можно считать признанным тот факт, что КК не смогут полностью вытеснить классические компьютеры, то есть идеология одноатомных, кластерных или супрамолекулярных булевых вентилей сохранит свою актуальность и в дальней перспективе. Поэтому ближайшая область практического использования КК - это проблемно- и алгоритмически ориентированные и, в частности, криптографические системы, для которых уже имеется квантовый криптографический протокол ВВ84С (США [206]).
Уникальность квантовых криптографических систем вытекает из возможности нахождения таких систем в запутанных состояниях [94, 207]. Пусть имеется два двухуровневых кубита А и В, например, молекула цитозина с двумя ядерными спинами  . Такая квантовая система может находиться в 4 четырехкомпонентных базисных состояниях, образуемых прямым произведением состояний отдельных кубитов:
. Такая квантовая система может находиться в 4 четырехкомпонентных базисных состояниях, образуемых прямым произведением состояний отдельных кубитов:
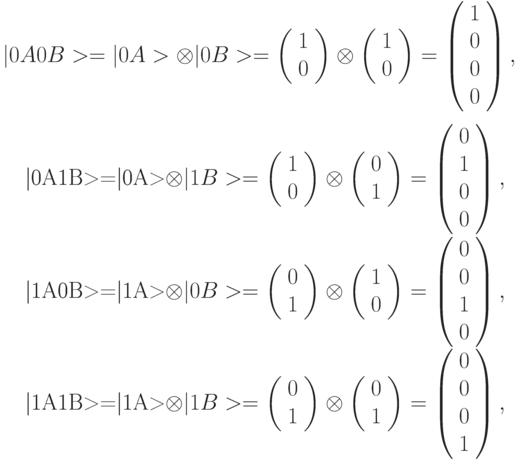
В общем случае чистое состояние такой квантовой системы описывается суперпозицией вида:
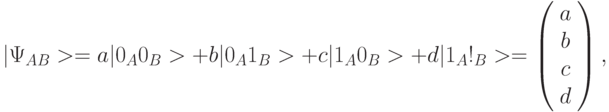
где  - скалярное произведение векторов состояний.
- скалярное произведение векторов состояний.
При  состояние квантовой системы несепарабельно и (7.9) невозможно представить в виде прямого произведения независимых состояний кубитов
состояние квантовой системы несепарабельно и (7.9) невозможно представить в виде прямого произведения независимых состояний кубитов 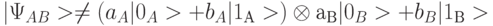 . Это значит, что в системе из 2 кубитов возникает нелокальная корреляция, свойственная только квантовой системе и невоспроизводимая в классических физических системах. Для такой квантовой системы оператор плотности
. Это значит, что в системе из 2 кубитов возникает нелокальная корреляция, свойственная только квантовой системе и невоспроизводимая в классических физических системах. Для такой квантовой системы оператор плотности 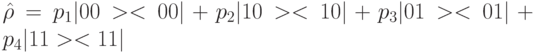 , где
, где 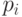 - вероятность
- вероятность  -го состояния в рассматриваемом представлении
-го состояния в рассматриваемом представлении 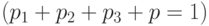 .
.
Такое несепарабельное состояние квантовой системы считается запутанным и при 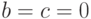 ,
,  его называют состоянием "шре-дингеровского кота", а при
его называют состоянием "шре-дингеровского кота", а при 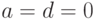 ,
, 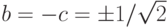 - синглетной EPR (Einstein - Podolsky - Rosen)-парой:
- синглетной EPR (Einstein - Podolsky - Rosen)-парой:  .
.
Как и в случае чистых состояний, матрица плотности запутанного  -состояния
-состояния
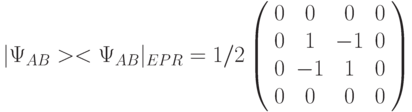
имеет одно отличное от нуля собственное значение, равное единице, и создать запутанные состояния можно с помощью нелокальных унитарных преобразований, которые одновременно действуют на два кубита.
В криптографических системах запутывание состояний используется для передачи (без перемещения кубитов - телепортации) от кубита-отправителя  неизвестного для него состояния кубита-сообщения
неизвестного для него состояния кубита-сообщения  кубиту-получателю
кубиту-получателю  . Это значит, что кубиту-отправителю неизвестны параметры
. Это значит, что кубиту-отправителю неизвестны параметры  и
и  состояния кубита-сообщения
состояния кубита-сообщения 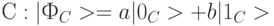 .
.
Чтобы осуществить телепортацию, необходимо с помощью оператора Адамара и 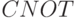 сформировать из состояний кубитов
сформировать из состояний кубитов  и
и 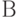 запутанное состояние типа
запутанное состояние типа  , которое известно отправителю и получателю и играет роль квантового канала передачи информации.
, которое известно отправителю и получателю и играет роль квантового канала передачи информации.
Общее состояние квантовой системы, которая включает само сообщение и канал его передачи, можно представить: 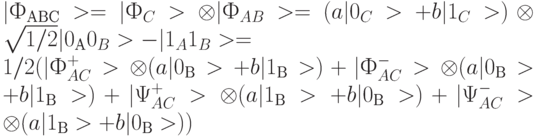 ,
Где
,
Где  и
и  -компоненты ортонормированного базиса Белла, построенного на состояниях кубитов
-компоненты ортонормированного базиса Белла, построенного на состояниях кубитов  и
и  , относящихся только к отправителю
, относящихся только к отправителю  . На приемном конце каждому из этих составляющих соответствует определенное состояние кубита
. На приемном конце каждому из этих составляющих соответствует определенное состояние кубита 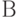 , которое по-своему зависит от параметров
, которое по-своему зависит от параметров  и
и  , но тем не менее позволяет восстановить исходное сообщение
, но тем не менее позволяет восстановить исходное сообщение 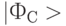 .
.
Поэтому, чтобы создать такой канал передачи информации, отправитель, получив неизвестное ему сообщение 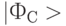 , измеряет запутанное состояние двух своих кубитов в базисе Белла, то есть проецирует
, измеряет запутанное состояние двух своих кубитов в базисе Белла, то есть проецирует 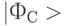 на состояние в этом базисе, и после этого сообщает получателю результаты измерения. Получатель на основе принятого сообщения и известного ему состояния кубита
на состояние в этом базисе, и после этого сообщает получателю результаты измерения. Получатель на основе принятого сообщения и известного ему состояния кубита 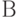 имеет возможность восстановить неизвестное отправителю сообщение
имеет возможность восстановить неизвестное отправителю сообщение 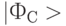 .
.
Пусть отправитель получил проекцию 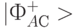 и сообщил об этом получателю по открытому каналу связи. Это значит, что отправитель в результате такого белловского измерения редуцировал исходное состояние двух кубитов отправителя
и сообщил об этом получателю по открытому каналу связи. Это значит, что отправитель в результате такого белловского измерения редуцировал исходное состояние двух кубитов отправителя  и
и  и одного кубита получателя
и одного кубита получателя 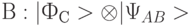 в состояние
в состояние 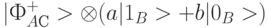 . Тем самым отправитель сообщил получателю, чем полученное состояние кубита
. Тем самым отправитель сообщил получателю, чем полученное состояние кубита 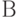 отличается от отправленного состояния кубита
отличается от отправленного состояния кубита  и какую операцию необходимо выполнить над кубитом
и какую операцию необходимо выполнить над кубитом 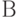 , чтобы идентифицировать отправленное состояние кубита
, чтобы идентифицировать отправленное состояние кубита  . Для этого достаточно выполнить локальную унитарную операцию
. Для этого достаточно выполнить локальную унитарную операцию 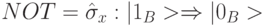 или
или  . В нашем случае отправитель получил запутанное состояние
. В нашем случае отправитель получил запутанное состояние 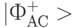 , поэтому полученное состояние будет совпадать с отправленным.
, поэтому полученное состояние будет совпадать с отправленным.
Если отправитель получил запутанное состояние 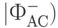 , то это значит, что нужно выполнить преобразование Паули вида
, то это значит, что нужно выполнить преобразование Паули вида  или
или 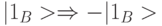 . Аналогично можно определить тип операции, которую необходимо выполнить на приемном конце для остальных вариантов идентификации запутанного состояния на приемном конце. В результате квантовая схема телепортации принимает вид
. Аналогично можно определить тип операции, которую необходимо выполнить на приемном конце для остальных вариантов идентификации запутанного состояния на приемном конце. В результате квантовая схема телепортации принимает вид
где ВL - белловское измерение, а двойная линия соответствует передаче сообщений по открытому каналу связи.
Кроме рассмотренных экспериментальных КК уже существуют достаточно реалистические проекты твердотельных КК, которые не обладают перечисленными выше принципиальными физико-техническими ограничениями, но их воплощение требует прогресса в нанотехнологии.
Один из проектов КК [186] на основе эффекта Холла использует двумерный электронный газ (2DEG) в магнитном поле H, который при целом заполнении уровней Ландау является недиссипативным, так как его магнитное сопротивление приближается к нулю. Это позволяет рассчитывать на то, что когерентность 2DEG будет высокой (необходимое условие существования КК ). В этом проекте кубитами являются полуцелые спины ядер, помещенных в 2DEG, а управление их состоянием осуществляется подачей радиочастотных импульсов, обеспечивающих прямой (селективный) доступ к каждому кубиту за счет различных частот полуцелых спинов ядер. В результате каждый кубит имеет свой ядерный магнитный резонанс, а система кубитов является гетерогенной. Удовлетворяющих перечисленным требованиям веществ в таблице Менделеева - десятки. Взаимодействие кубитов (ядерных спинов) между собой предлагается осуществлять с помощью сверхтонкого взаимодействия электронов с магнитными моментами ядер.
При этом электроны должны двигаться по лармо-ровским орбитам. Основная проблема - экспоненциальное ослабление такого взаимодействия для расстояний, превышающих квантовый ларморовский радиус 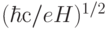 , который обычно равен
, который обычно равен  Одна из проблем создания такого КК - это управление (включение и выключение) такими взаимодействиями, которая пока решается за счет включения примесей между ядрами. Ионизация этих примесей импульсами света приводит к временной локальной некогерентности в электронной системе, которая и блокирует взаимодействие.
Одна из проблем создания такого КК - это управление (включение и выключение) такими взаимодействиями, которая пока решается за счет включения примесей между ядрами. Ионизация этих примесей импульсами света приводит к временной локальной некогерентности в электронной системе, которая и блокирует взаимодействие.
Схема другого реалистичного КК (Австрия [186]) использует кубиты на основе изотопа фосфора 31P с полуцелым ядерным спином. Атомы фосфора размещаются на поверхности кремния по СТМ-технологии.