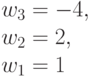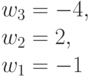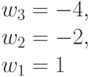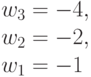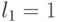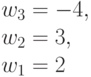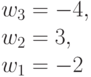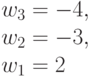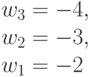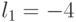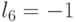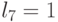Нейрофизиологический и формально-логический базис нейроподобных вычислений
4.7. Теоретико-групповая модель формального нейрона как операционное ядро компиляции на квантовый уровень организации вычислений
За всю историю развития вычислительной техники интерес к нейро-компьютерным технологиям возрастал каждый раз, когда наступал либо застой в архитектурных решениях ЭВМ, либо прогресс в элементной базе. Современный повышенный интерес к нейрокомпьютерным технологиям [84, 87-89] фактически совпал по времени с наметившимся прорывом в области нанотехнологий, где в качестве "рабочего тела" выступают квантовые системы различной степени сложности: от одноэлектронных транзисторов [92, 93] и до квантовых компьютеров [94]. Схемотехнический парадокс традиционной нейроподобной элементной базы [68] вызван тем, что в этом случае логические функции реализуются через арифметические. Это предопределяет повышенные затраты традиционных логических вентилей, которые сначала расходуются на реализацию арифметических преобразований формальных нейронов и только после этого на реализацию логических преобразований блоков и устройств вычислительной техники, построенных на формальных нейронах. Объединение возможностей нейрокомпью-терных программных [88] и нанотехнологических [95] инструментальных платформ позволяет преодолеть или хотя бы ослабить последствия этого парадокса за счет прямого отображения функций пользователя на квантовые системы, фундаментальные свойства которых определяются и описываются
различными группами симметрий [96]. Так, правила отбора [97] задают возможные квантовые переходы для атомов, молекул, взаимодействующих элементарных частиц и т. д. Эти правила напрямую связаны с симметрией квантовых систем, с помощью которой определяют неизменные (инвариантные) свойства этих систем при определенных преобразованиях координат и времени. В частности, в квантовой механике допустимы только те переходы из одного состояния в другое, которые не нарушают законы сохранения энергии, импульса, электрического заряда и т. д.
Переход к теоретико-групповым моделям формальных нейронов позволяет сохранить традиционную схему кремниевой компиляции [98, 99] на основе библиотек "стандартных элементов", которые в данном случае должны реализовать не булевы функции, а "элементарные группы симметрий". Поэтому нейрокомпилятор должен представить задание пользователя в фиксированном теоретико-групповом операционном базисе, реализуемом на технологическом уровне производства и эксплуатации компьютеров с нано- или супрамолекулярной элементной базой. Отсюда и встает задача доказательства не только возможности, но и эффективности использования теоретико-групповых моделей классических (много)поро-говых элементов в задачах оптимального синтеза нейроподобных ЭВМ. При этом совершенно безразлично, в каком операционном базисе будет работать ЭВМ с нано- или супрамолекулярной элементной базой, так как нейроподобный операционный базис фактически используется и на уровне "элементарных действий" ЭВМ классических архитектур (см. "Теория вычислений и машины Тьюринга" ).
Учитывая быстрое нарастание размерности задач оптимального синтеза (много)пороговых моделей до гиперкомбинаторной, ограничим конкретные примеры и характеристики теоретико-групповой модели классом булевых функций от  переменных [100].
переменных [100].
Для булевых функций параметры (М)ПМ (4.4) принимают значения 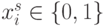 ;
; 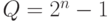 ;
; 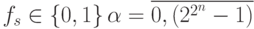 , и поэтому оператор линейной свертки можно записать:
, и поэтому оператор линейной свертки можно записать:
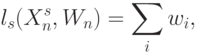 |
( 4.27) |
где суммирование ведется по тем  , для которых
, для которых 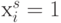 , то есть в случае булевых функций входной вектор
, то есть в случае булевых функций входной вектор 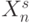 используется как "маска", определяющая правило "ассоциативного" суммирования компонент весового вектора
используется как "маска", определяющая правило "ассоциативного" суммирования компонент весового вектора  .
.
Не изменяя значений конечного множества весовых коэффициентов  , их можно расположить в произвольном порядке (по
, их можно расположить в произвольном порядке (по  ) над компонентами входного вектора
) над компонентами входного вектора 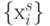 , что соответствует группе подстановок
, что соответствует группе подстановок 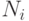 (порядок группы
(порядок группы  !). В результате изменятся правила суммирования весовых коэффициентов в (4.27), что индуцирует изоморфную группу подстановок
!). В результате изменятся правила суммирования весовых коэффициентов в (4.27), что индуцирует изоморфную группу подстановок 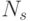 значений свертки
значений свертки 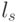 , а вместе с ними и индексов
, а вместе с ними и индексов  на скалярной оси
на скалярной оси 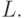 Например, при
Например, при  (табл. 4.8) получим 6 подстановок индексов s в упорядоченной по возрастанию последовательности значений свертки
(табл. 4.8) получим 6 подстановок индексов s в упорядоченной по возрастанию последовательности значений свертки 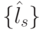 , из которых одна соответствует лексикографическому порядку
, из которых одна соответствует лексикографическому порядку 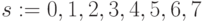 .
.
 |
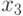 |
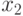 |
 |
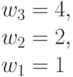 |
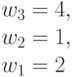 |
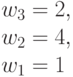 |
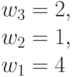 |
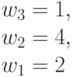 |
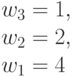 |
|||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
 |
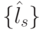 |
 |
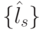 |
 |
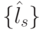 |
 |
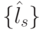 |
 |
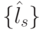 |
||||
| 0 | 0 | 0 | 0 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 1 | 0 | 0 | 1 | 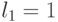 |
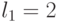 |
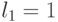 |
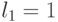 |
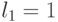 |
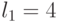 |
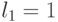 |
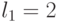 |
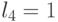 |
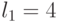 |
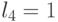 |
| 2 | 0 | 1 | 0 |  |
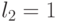 |
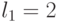 |
 |
 |
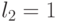 |
 |
 |
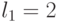 |
 |
 |
| 3 | 0 | 1 | 1 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 4 | 1 | 0 | 0 | 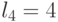 |
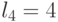 |
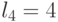 |
 |
 |
 |
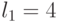 |
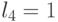 |
 |
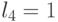 |
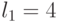 |
| 5 | 1 | 0 | 1 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 6 | 1 | 1 | 0 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 7 | 1 | 1 | 1 | 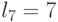 |
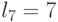 |
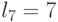 |
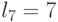 |
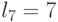 |
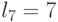 |
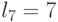 |
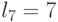 |
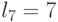 |
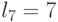 |
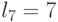 |
Группа инверсии знаков  при неизменных абсолютных значениях компонент весового вектора
при неизменных абсолютных значениях компонент весового вектора  индуцирует изоморфную группу подстановок
индуцирует изоморфную группу подстановок 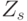 (табл. 4.9) значений свертки
(табл. 4.9) значений свертки 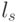 , а с ними и индексов s на скалярной оси
, а с ними и индексов s на скалярной оси  .
.
 |
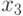 |
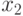 |
 |
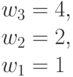 |
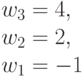 |
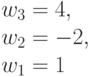 |
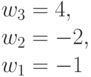 |
|||
|---|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
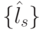 |
 |
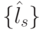 |
||||
| 0 | 0 | 0 | 0 |  |
 |
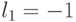 |
 |
 |
 |
 |
| 1 | 0 | 0 | 1 | 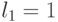 |
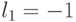 |
 |
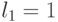 |
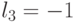 |
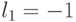 |
 |
| 2 | 0 | 1 | 0 |  |
 |
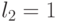 |
 |
 |
 |
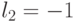 |
| 3 | 0 | 1 | 1 |  |
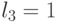 |
 |
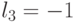 |
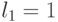 |
 |
 |
| 4 | 1 | 0 | 0 | 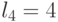 |
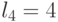 |
 |
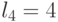 |
 |
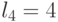 |
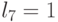 |
| 5 | 1 | 0 | 1 |  |
 |
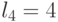 |
 |
 |
 |
 |
| 6 | 1 | 1 | 0 |  |
 |
 |
 |
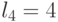 |
 |
 |
| 7 | 1 | 1 | 1 | 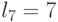 |
 |
 |
 |
 |
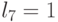 |
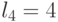 |
На основе данных таблиц 4.8 и 4.9 можно сформировать подстановки индексов  , которые отвечают прямому произведению групп
, которые отвечают прямому произведению групп 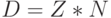 . Элементы групп D_{s} индуцируются элементами группы переименования переменных
. Элементы групп D_{s} индуцируются элементами группы переименования переменных 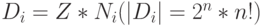 .
.
Как показано в разделе 4.7, в непрерывной группе вращений весового вектора 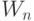 имеется еще один источник подстановок значений свертки
имеется еще один источник подстановок значений свертки 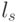 , а вместе с ними и индексов
, а вместе с ними и индексов  на скалярной оси
на скалярной оси 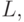 который связан с инверсией отношения "больше-меньше" между различными комбинациями значений компонент весового вектора
который связан с инверсией отношения "больше-меньше" между различными комбинациями значений компонент весового вектора  . Чтобы получить множество подстановок этого типа, достаточно наложить ограничение
. Чтобы получить множество подстановок этого типа, достаточно наложить ограничение 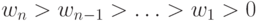 . Тогда при
. Тогда при  между значениями компонент весового вектора могут установиться отношения
между значениями компонент весового вектора могут установиться отношения 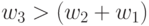 и
и 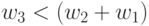 .
.
В результате преобразование (4.27) компонент весового вектора 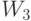 порождает группу подстановок
порождает группу подстановок 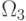 из двух элементов: тождественная подстановка с лексикографическим порядком следования индексов
из двух элементов: тождественная подстановка с лексикографическим порядком следования индексов 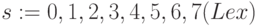 и подстановка вида
и подстановка вида 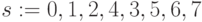 . Прямое произведение групп
. Прямое произведение групп  также является группой подстановок порядка
также является группой подстановок порядка  (совокупность подстановок таблиц 4.9 и 4.10).
(совокупность подстановок таблиц 4.9 и 4.10).
Продолжение табл. 4.9
Таким образом, для достоверной оценки функций качества (4.6) и (4.7) в случае  необходимо иметь всего два образующих весовых вектора
необходимо иметь всего два образующих весовых вектора 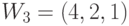 и
и 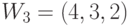 . Остальные весовые вектора являются производными и их можно получить перестановками и инверсиями знаков целочисленных компонент, которые и порождают все многообразие подстановок индексов
. Остальные весовые вектора являются производными и их можно получить перестановками и инверсиями знаков целочисленных компонент, которые и порождают все многообразие подстановок индексов  , напрямую влияющих на размерность вектора порогов, а значит, и на численные значения функций качества (4.6) и (4.7).
, напрямую влияющих на размерность вектора порогов, а значит, и на численные значения функций качества (4.6) и (4.7).
 |
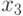 |
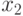 |
 |
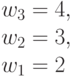 |
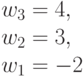 |
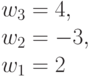 |
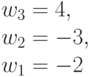 |
||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
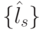 |
 |
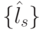 |
 |
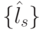 |
||||
| 0 | 0 | 0 | 0 |  |
 |
 |
 |
 |
 |
 |
 |
| 1 | 0 | 0 | 1 | 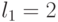 |
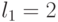 |
 |
 |
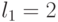 |
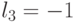 |
 |
 |
| 2 | 0 | 1 | 0 |  |
 |
 |
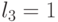 |
 |
 |
 |
 |
| 3 | 0 | 1 | 1 |  |
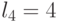 |
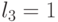 |
 |
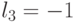 |
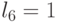 |
 |
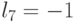 |
| 4 | 1 | 0 | 0 | 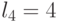 |
 |
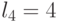 |
 |
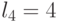 |
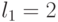 |
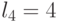 |
 |
| 5 | 1 | 0 | 1 |  |
 |
 |
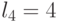 |
 |
 |
 |
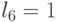 |
| 6 | 1 | 1 | 0 |  |
 |
 |
 |
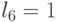 |
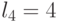 |
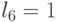 |
 |
| 7 | 1 | 1 | 1 |  |
 |
 |
 |
 |
 |
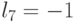 |
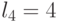 |
Поэтому на этапе абстрактного синтеза (много)пороговых моделей оператор линейной свертки с непрерывными значениями весовых коэффициентов можно заменить конечной группой преобразований  , которая представляет собой прямое произведение следующих групп: подстановок индексов
, которая представляет собой прямое произведение следующих групп: подстановок индексов  , индуцированных оператором (4.27), ассоциативного суммирования компонент весового вектора
, индуцированных оператором (4.27), ассоциативного суммирования компонент весового вектора  с отношением "больше-меньше", группой инверсий знака и группой подстановок (по индексу
с отношением "больше-меньше", группой инверсий знака и группой подстановок (по индексу  ) множества компонент весового вектора.
) множества компонент весового вектора.
Продолжение табл. 4.10
Для 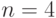 множество
множество 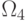 трансформируется в дистрибутивную структуру, которая представляет собой теоретико-множественное объединение 13 двухэлементных групп подстановок, каждая из которых содержит тождественную и обратную по отношению к себе подстановки. Теоретико-множественное пересечение всех двухэлементных групп дистрибутивной структуры
трансформируется в дистрибутивную структуру, которая представляет собой теоретико-множественное объединение 13 двухэлементных групп подстановок, каждая из которых содержит тождественную и обратную по отношению к себе подстановки. Теоретико-множественное пересечение всех двухэлементных групп дистрибутивной структуры 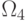 содержит единственную тождественную подстановку
содержит единственную тождественную подстановку