Нейрофизиологический и формально-логический базис нейроподобных вычислений
Графически перцептрон можно представить тремя типами схем: функциональной, структурной и символической (рис. 4.19).
Функциональная схема детализирует связи между элементами различных слоев перцептро-на: сенсорного, ассоциативного и реагирующего. В структурной схеме весь сенсорный слой представлен одним элементом, элементы ассоциативного слоя детализируются до диаграмм Венна и связей с элементами реагирующего слоя. Символьная диаграмма идентифицирует только типы связей, существующих между элементами перцептрона: от  -типа к
-типа к  -типу, от
-типу, от  -типа к
-типа к 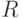 -типу и связи элементов
-типу и связи элементов  -типа между собой.
-типа между собой.
Проведенная Ф. Розенблаттом "формализация" нервного субстрата и правил его функционирования носит скорее инженерный, чем строгий математический характер и, как модель Мак-Каллока - Питтса, включает два уровня:
- уровень "элементов", в качестве которых выступают функционально ориентированные формальные нейроны
 -,
-,  - и
- и 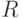 -типа, порождаемые ими реакции и связи, обеспечивающие взаимодействие между элементами;
-типа, порождаемые ими реакции и связи, обеспечивающие взаимодействие между элементами; - уровень "системы", функционирование которой регламентируется правилами взаимодействия с внешней средой и правилами "выживания", заложенными в систему управления подкреплением, в том числе и в условиях прямого взаимодействия с внешней средой в процессе обучения, которое в таких условиях становится неотъемлемой фазой жизненного цикла.
Но в отличие от моделей Мак-Каллока - Питтса в перцептроне:
- структурно-параметрическую адаптацию сети формальных нейронов можно свести к чисто параметрической адаптации, обнулив весовые коэффициенты незадействованных, но реально существующих связей как между элементами различных слоев, так и принадлежащими одному слою;
- стохастический характер распространения сигналов через синапти-ческую щель отражен флуктуациями весовых коэффициентов
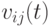 , участвующих в формировании взвешенных сумм входных возбуждений (см. определения 16 и 23);
, участвующих в формировании взвешенных сумм входных возбуждений (см. определения 16 и 23); - фактор временной задержки как на распространение по нервной соединительной ткани, так и в синапсе стал функционально значимым (см. определение 12).
Закладывая основы нейродинамики, Ф. Розенблатт стремился создать аналог статистической физикой для эффективного анализа реальных психофизиологических процессов. Но в итоге ему удалось распространить апробированные в термодинамике статистические методы на качественно новую область "нефизических" исследований, связанных с моделированием процессов обучения вообще и распознавания образов в частности [71]. Главная специфика задач обучения и распознавания - это неэффективность алгоритмических методов из-за постоянно изменяющегося комплекса внешних условий и неоднозначности возможных, но эквивалентных в некотором смысле реакций, что противоречит базовым положениям математики, в том числе и вычислительной [45]. Скрытый парадокс задач обучения "машин" состоит в необходимости применения формальных методов и средств к самому процессу формализации, что требует включения этого процесса в полный "жизненный цикл" ра боты "машины". В результате система обучения с подкреплением типа рис. 4.18 является практически единственным средством установления и постоянной модификации условных причинно-следственных связей, действительных только для фиксированного на некотором интервале времени комплекса внешних условий.
Несмотря на большие достижения в области построения (само)обу-чающихся машин и систем [2, 16, 17, 33, 34], особенно решающих задачи распознавания образов, классификации и идентификации [72-76], включить в их полный жизненный цикл все задачи формализации так и не удалось. В частности, открытым всегда остается вопрос перехода от реальных объектов и процессов к их математическим представителям - множествам и числам, то есть вопрос о том, что и чем измерять, лежит вне контура обучения и является прерогативой разработчика машины или системы распознавания, классификации и идентификации.
Поэтому типичной является следующая постановка задачи [72]. Пусть имеется набор 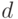 данных (образов), подлежащих классификации (распознаванию, идентификации) и представленных действительными (комплексными, целыми) числами
данных (образов), подлежащих классификации (распознаванию, идентификации) и представленных действительными (комплексными, целыми) числами 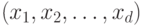 . Требуется найти разделяющую поверхность (рис. 4.20) для
. Требуется найти разделяющую поверхность (рис. 4.20) для 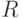 классов объектов
классов объектов 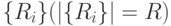 в
в 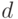 -мерном евклидовом пространстве
-мерном евклидовом пространстве 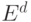 , точки которого представлены числами
, точки которого представлены числами 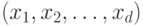 или векторами
или векторами 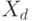 . Считается, что разделяющую поверхность можно полностью определить скалярными функциями
. Считается, что разделяющую поверхность можно полностью определить скалярными функциями 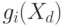 (дискриминантными функциями), такими, что
(дискриминантными функциями), такими, что 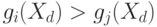 , если
, если 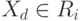 , где
, где 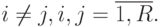 В нашем случае:
В нашем случае:  ,если
,если 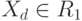 ;
;  , если
, если 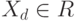 ; и
; и  , если
, если 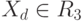 , где
, где 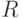 - внешняя часть незаштрихованной области.
- внешняя часть незаштрихованной области.
Отвечающая такой постановке задачи структурная схема системы классификации имеет вид
рис. 4.21-а [72], которая трансформируется в схему простейшего классификатора, разбивающего множество объектов на два класса (рис. 4.21-б -  ). В последнем случае блок выбора максимума вырождается в пороговый элемент, работающий по правилу:
). В последнем случае блок выбора максимума вырождается в пороговый элемент, работающий по правилу: 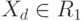 , если
, если 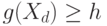 , и
, и 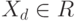 , если
, если 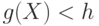 , где
, где  - значение порога. Отсюда, настроить (адаптировать) классификаторы
рис. 4.18 на конкретное множество классифицируемых (разделяемых, различаемых и т. п.) объектов - это найти множество дискриминантных функций
- значение порога. Отсюда, настроить (адаптировать) классификаторы
рис. 4.18 на конкретное множество классифицируемых (разделяемых, различаемых и т. п.) объектов - это найти множество дискриминантных функций 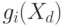 с однозначно определенными максимумами для всей совокупности объектов
с однозначно определенными максимумами для всей совокупности объектов 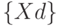 и классов
и классов  .
.
Выбор дискриминантных функций обычно представляет центральную задачу обучения системы классификации (идентификации, распознавания образов), что предполагает отсутствие полной априорной информации о классифицируемых объектах и/или вариабельных условиях, при которых будет протекать классификация.
Отличают [72] параметрические и непараметрические методы обучения, к первым из которых прибегают, если априори известны "почти все" параметры, характеризующие принадлежность каждого объекта 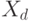 к соответствующему классу
к соответствующему классу 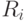 . Поэтому в данном случае обучающая выборка используется для нахождения значений этих параметров, по которым в дальнейшем строятся дискриминантные функции. Например, априори известно, что объекты первого класса группируются около точки
. Поэтому в данном случае обучающая выборка используется для нахождения значений этих параметров, по которым в дальнейшем строятся дискриминантные функции. Например, априори известно, что объекты первого класса группируются около точки  или, что одно и то же, вектора
или, что одно и то же, вектора 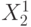 , а объекты второго класса - вокруг точки
, а объекты второго класса - вокруг точки  или вектора
или вектора  соответственно (рис. 4.22).
соответственно (рис. 4.22).
Точные численные значения типичных (эталонных и т. п.) представителей соответствующего класса  и
и  считаются неизвестными и рассматриваются как параметры, вариация которых позволяет получить оценки для
считаются неизвестными и рассматриваются как параметры, вариация которых позволяет получить оценки для 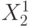 и
и  , которые и находятся во время обучения. В качестве таких оценок обычно используются всевозможные "средние", определяемые как центры "масс", "тяжести" и т. п. классифицируемых подмножеств (см.
рис. 4.20). Зная оценки
, которые и находятся во время обучения. В качестве таких оценок обычно используются всевозможные "средние", определяемые как центры "масс", "тяжести" и т. п. классифицируемых подмножеств (см.
рис. 4.20). Зная оценки  и
и  , можно построить дискриминантную поверхность. В данном случае она представляет собой перпендикулярную линию, проходящую через середину отрезка между центральными точками классов
, можно построить дискриминантную поверхность. В данном случае она представляет собой перпендикулярную линию, проходящую через середину отрезка между центральными точками классов 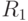 и
и 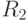 , которой соответствует дискриминантная функция
, которой соответствует дискриминантная функция
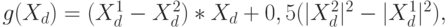
где 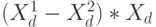 - скалярное произведение векторов (
- скалярное произведение векторов ( 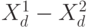 ) и
) и 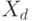 ,
а
,
а 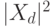 - квадрат модуля соответствующего вектора.
- квадрат модуля соответствующего вектора.
Таким образом, чем выше репрезентативность обучающей выборки, тем достоверней определяются центры подмножеств классифицируемых объектов и тем точнее и достоверней работает система классификации. Отсюда, перцептронные модели и основанные на них системы распознавания образов не отменяют знаний о предметной области (свойствах классифицируемых объектов и их подмножеств), а только изменяют форму представления этих знаний,которые тем достоверней, чем более представительна обучающая выборка.
Описанный подход к построению систем распознавания образов послужил толчком к развитию теории распознавания образов [73-76], в рамках которой классификация по критерию минимума расстояния уже предстала как частный случай теории статистических решений и синтаксического анализа последовательностей символов. Успехи в теории и практике распознавания образов в какой-то мере отодвинули на второй план главную задачу нейродинамики, которая должна была дать ответ на вопрос о механизмах установления причинно-следственных связей в живых системах. Для этого необходимо формализовать процессы преобразования информации, что требует построения информационных эквивалентов традиционных для физики скалярных и особенно векторных понятий, таких как масса, энергия, импульс, сила, потоки массы, обобщенные силы и т. п. В частности, "векторизация" информационных процессов требует объективной оценки направления приложения "информационных усилий", что сопряжено с прагматической и/или семантической оценкой преобразований входной информации в выходную, которую, по П.К. Анохину, невозможно получить без формализации цели поведения системы и достигнутого ею полезного приспособительного эффекта.

![Общая схема экспериментальной системы [71]](/EDI/14_06_16_2/1465856498-31733/tutorial/593/objects/4/files/04_18.gif)
![Схемы представления перцептрона [71]](/EDI/14_06_16_2/1465856498-31733/tutorial/593/objects/4/files/04_19.gif)
![Пример разделяющей поверхности для R = 3 и d = 2 [72]](/EDI/14_06_16_2/1465856498-31733/tutorial/593/objects/4/files/04_20.gif)
![Модели классификаторов [72]](/EDI/14_06_16_2/1465856498-31733/tutorial/593/objects/4/files/04_21.gif)
![Линейная разделяющая поверхность, зависящая от параметров множеств объектов [72]](/EDI/14_06_16_2/1465856498-31733/tutorial/593/objects/4/files/04_22.gif)