Рекуррентные сети: Ассоциативная память

Версии прототипа

Итак, структура аттракторов в модели Хопфилда может допускать различные содержательные интерпретации. В том случае, когда она совпадает со структурой запоминаемых образов мы говорим об ассоциативной памяти (пассивной). Если, напротив, в сети формируется единственный аттрактор, в каком-то смысле являющийся прототипом этих образов, то проявляется способность сети к обобщению (generalization). В общем же случае структура аттракторов сети настолько сложна, что на первый взгляд не допускает какой-либо наглядной трактовки. Действительно, такая трактовка должна быть настолько универсальной, чтобы включать режимы запоминания и обобщения в качестве предельных случаев. Тем не менее она возможна и опирается на рассуждения, которые приводятся в данном разделе.

Начнем с рассмотрения сети Хопфилда, в память которой, согласно правилу Хебба, записан только один образ 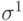. В этом случае синаптические связи определяются выражением

У такой сети есть только два зеркально симметричных стационарных состояния 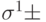. Если она перейдет в одно из них, то величина энергии в минимуме составит

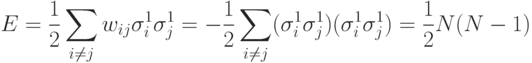
Заметим, что все связи в сети дают в энергию одинаковый отрицательный вклад и поэтому являются не фрустрированными. Напомним, что условием фрустрации связи в состоянии сети является неравенство .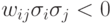

Именно это условие не выполняется ни для одной связи в сети с записанным единственным образом. Мы можем трактовать подобную ситуацию так, что сеть с одним записанным в нее образом точно воспроизводит его в виде своего аттрактора (с точностью до зеркального отражения), и если мы выберем в этой сети случайную связь, то вероятность ее фрустрации будет равна нулю.

Таким образом, сеть Хопфилда идеально приспособлена для хранения единственного образа.

Рассмотрим теперь следующую систему (см. рисунок 5.6). Пусть в Хопфилдовской сети-передатчике (слева) записан единственный образ 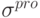, который нам неизвестен. Этот образ многократно передается в Хопфилдовскую сеть-приемник (справа) в виде сообщения через канал с шумом. При его прохождении образ 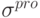искажается так, что некоторые компоненты кодирующего его вектора меняют свой знак на противоположный.

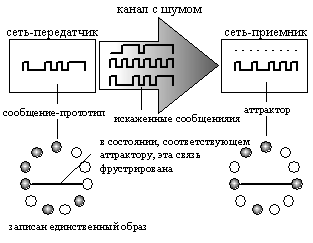
Рис. 5.6. Вверху: интерпретация стационарных состояний в сети Хопфилда как локально наиболее правдоподобных версий сообщения, многократно переданного сетью-передатчиком в сеть-приемник через канал с шумом. Внизу: сети с записанным единственным сообщением прототипом (слева) и со всеми искаженными версиями этого сообщения (справа)

Задача сети-премника состоит в том, чтобы имея P полученных сообщений 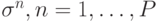восстановить исходное сообщение 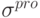. Исходя из полученных сообщений, оценим вероятность того, что в исходном сообщении компоненты 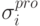и 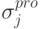имеют одинаковое или противоположные значения. Для этого нужно просто подсчитать, в скольких из P сообщений произведения положительны или отрицательны и отнести это число к полному числу сообщений. Формально эти вероятности можно записать как

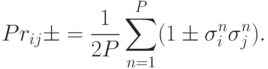
Вспоминая выражение для правила Хебба, убеждаемся что если сообщения 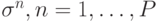, полученные сетью-приемником, сформируют свои связи в соответствие с ним, то тогда

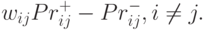
Используя последнее соотношение, преобразуем выражение для энергии состояния в сети-приемнике к виду

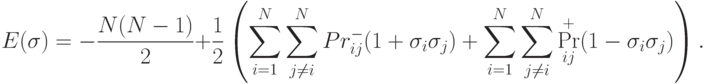
Поскольку мы не знаем точного вида сообщения 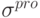, записанного в связях сети-передатчика, то мы не знаем и величин этих связей. Однако, мы можем задаться следующим вопросом: если состояние сети-передатчика совпадает с состоянием сети-приемника 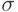, то какова вероятность, что случайно выбранная связь в сети-передатчике окажется фрустрированной. Легко увидеть, что эта вероятность равна

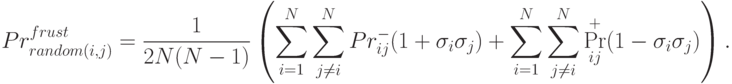
Таким образом, энергия состояния сети-приемника с точностью до постоянных множителя и слагаемого совпадает с вероятностью фрустрации случайно выбранной связи в сети-передатчике, оцененной по полученным от нее сообщениям.

Однако в сети-передатчике записано лишь одно сообщение, и вероятность фрустрации связей в ней равна нулю. Но поскольку ни сообщение, ни соответствующие ему связи сети-передатчика нам не известны, мы можем лишь пытаться найти такое состояние сети-приемника, которое хотя бы локально минимизирует эту вероятность. Подобные состояния были бы локально наилучшими версиями сообщения, посылаемого сетью-передатчиком. А так как вероятность нахождения фрустрированной связи в передатчике связана с энергией состояния в приемнике, то такими наилучшими версиями как раз и окажутся состояния, соответствующие энергетическим минимумам сети-приемника. Таким образом все аттракторы сети Хопфилда, связи которой сформированы согласно правилу Хебба, исходя из набора обучающих векторов , могут трактоваться как наиболее вероятные версии некоторого сообщения, переданного P раз через канал с шумом и представленных заучиваемыми векторами.

Подобный подход устраняет деление состояний памяти на истинные и ложные, давая им единую интерпретацию. В такой трактовке функционирование сети Хопфилда в качестве пассивной памяти соответствует случаю, когда шум в канале очень велик, т.е. все принимаемые сетью сообщения некоррелированы. Это не дает ей возможности выделить из них сообщения и, рассматривая их как равноправные его версии, сеть генерирует аттрактор в каждой точке N-мерного пространства . Если же, напротив, шум в канале невелик, т.е. все запоминаемые векторы мало отличаются от передаваемого сообщения, в сети вырабатывается его единственная версия.

Хотя первоначально сеть Хопфилда привлекалась для объяснения свойств ассоциативной памяти, можно привести множество различных примеров ее применения и для выделения зашумленного сигнала-прототипа. В качестве одного из таких примеров мы рассмотрим один - поиск промоторов в ДНК

Пример: поиск промоторов в ДНК

Промоторами называются области четырехбуквенной последовательности ДНК (построенной из нуклеотидов A,T,G,C), которые предшествуют генам. Эти области состоят из 50-70 нуклеотидов и распознаются специальным белком РНК-полимеразой. Полимераза связывается с промотором и транскрибирует ее (расплетает на две нити). У кишечной палочки, например, обнаружено около трехсот различных промоторов. Несмотря на различие, эти области имеют некоторые похожие участки, которые представляют собой как бы искажения некоторых коротких последовательностей нуклеотидов (например, бокс Гильберта - TTGACA и бокс Прибноу - TATAAT). Поэтому основные методы распознавания промоторов основываются на представлении о консенсус-последовательности: некотором идеальном промоторе, искажениями которого являются реальные промоторы. Близость некоторой последовательности к консенсус-последовательности оценивается по значению некоторого индекса гомологичности. Очевидно, что представление о версии-прототипа в теории минимизирующих энергию нейронных

сетей прямо соответствует представлению о консенсус-последовательности.

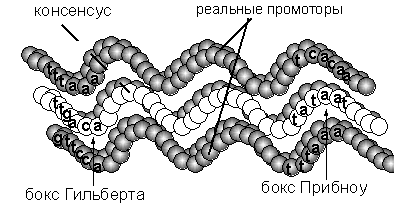
Рис. 5.7. Идеальный промотор - консенсус-последовательность (в середине) является аналогом единственной версии прототипа - аттрактора в сети Хопфилда, выработанной в ней при записи зашумленных сообщений (аналогов реальных промоторов: сверху и снизу). Аналогом гомологического индекса, определяющего близость реальных промоторов к консенсус-последовательности, является энергия состояния сети

Поэтому сеть Хопфилда, например, может непосредственно использоваться для ее поиска. Более того, оказывается, что энергия состояния сети может использоваться в качестве аналога гомологического индекса при оценке близости последовательности промотора к консенсус-последовательности. Такой подход позволил создать новый, весьма эффективный нейросетевой метод поиска промоторов. Аналогичный подход может использоваться для поиска скрытых повторов в ДНК и реконструкции эволюционных изменений в них.

Хотя молекулярная генетика представляет собой достаточно специфическую область применения методов обработки информации, она часто рассматривается как показательный пример приложений такой информационной технологии, как Извлечение Знаний из Данных (Data Mining). Применение для этих целей нейросетевых методов мы рассмотрим более подробно в отдельной лекции.