Рекуррентные сети: Ассоциативная память
Пустые классы
Активная кластеризация
Итак, мы установили, что преобразование информации рекуррентными нейронными сетями минимизирующими энергию может приводить к появлению в их пространстве состояний аттракторов, далеких по форме от образов внешнего для сети окружения. Таким образом, в отличие от рассмотренной в прошлой лекции кластеризации, осуществляемой сетями без обратных связей, появляется возможность использовать рекуррентные сети для активной кластеризации, при которой сеть "творчески" относится к входным векторам, осуществляя нетривиальные обобщения поступающих на ее вход сигналов.
Теоретическим основанием такой активной кластеризации является отмеченное выше наблюдение, что все устойчивые состояния сети Хопфилда могут быть проинтерпретированы единым образом, как локально наилучшие версии одного сообщения, переданного через канал с шумом. Если предъявить сети эти сообщения, использованные для формирования ее связей, в качестве начальных состояний, она расклассифицирует их, отнеся к той или иной версии прототипа. (Такая классификация при асинхронной динамике будет в общем случае нечеткой - одно и то же начальное состояние в разных попытках может эволюционировать к разным аттракторам).
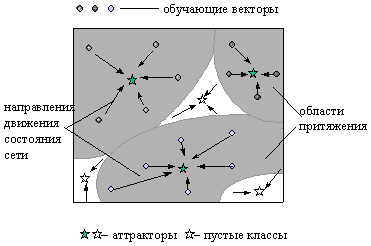
Однако, если исследовать все пространство состояний сети, предъявляя ей не ранее заучиваемые, а случайно сгенерированные векторы, то в нем могут обнаружиться такие аттракторы, которые не притягивают ни одного вектора из заучиваемого набора. Подобные аттракторы можно назвать пустыми классами, сформированными сетью. Понятие пустого класса не совпадает с понятием ложного состояний памяти. Последние не всегда описывает пустой класс. Например, когда в сети на основе слегка искаженных сообщений генерируется единственная версия сообщения, не совпадающая ни с одним из них (ложное состояние), но притягивающее все полученные сообщения (не пустой класс).
Аттракторы, являющиеся центрами притяжения состояний, относящихся к пустым классам, предоставляют нам совершенно новую информацию. Действительно, они предсказывают существование новых классов объектов, которые не имеют своих представителей в полученных сетью сообщениях.
Известным примером такой предсказательной категоризации является периодическая система элементов Менделеева, в которой изначально были определены три пустые клетки для впоследствии обнаруженных новых химических элементов. Итак, минимизирующие энергию нейронные сети типа сети Хопфилда могут использоваться для предсказания существования новых классов объектов.
Анализ голосований
В качестве иллюстрации приведем результаты кластеризации данных по голосованиям в ООН в 1969-1970гг. В данном примере анализировались голосования по 14 резолюциям для 19 стран. Сеть, производившая кластеризацию стран по степени схожести их голосований, состоит из нейронов, состояния которых представляют картину голосования одного из участников по отобранным 14 резолюциям (да и нет соотносились с бинарными состояниями нейронов). Этой сети предъявлялись результаты голосований 19 стран - членов ООН, которые сформировали матрицу связей сети по правилу Хебба. Результаты категоризации входных векторов (а тем самым - и соответствующих стран), этой нейронной приведены в таблице:
| Группа 1 | ранг | Группа 2 | ранг | Группа 3 | ранг | Группа 4 | ранг |
|---|---|---|---|---|---|---|---|
| США | 0 | Югославия | 2 | Болгария | 4 | ??? | 0 |
| Новая Зеландия | 2 | Кения | 2 | СССР | 5 | ||
| Великобритания | 3 | ОАР | 2 | Сирия | 6 | ||
| Албания | 4 | Дагомея | 9 | Танзания | 7 | ||
| Бразилия | 5 | Сенегал | 9 | ||||
| Норвегия | 5 | ||||||
| Мексика | 6 | ||||||
| Швеция | 7 | ||||||
| Венесуэла | 8 | ||||||
| Франция | 9 |
Все используемые при обучении страны разделились на три легко интерпретируемых класса (условно: "капиталистические", "неприсоединившиеся" и "социалистические"), то есть кодирующие их голосования векторы-состояния эволюционируют к одному из трех стационарных состояний (локально наилучших версий прототипа "страна - член ООН"). Хэммингово расстояние от соответствующих состояний до притягивающих их аттракторов приведено в колонках "ранг".
У сети, однако, имеется и четвертое стационарное состояние, не притягивающее ни один из 19 образов, используемых при построении матрицы связей сети. Это состояние может рассматриваться как описывающее совершенно новую группу стран, в которую не входят ни одна из рассматриваемых. Мы можем описать эту группу, изучив вид соответствующего аттрактора - центра пустого четвертого класса. Действительно, такое изучение легко выявляет тот факт, что представители этого нового класса должны были бы иметь по сравнению с учтенными странами совершенно особое мнение при голосовании по корейскому вопросу. Учитывая то, что ни Южная, ни Северная Корея до сих пор не представлены в ООН, интерпретация этого класса является прозрачной. Очевидно, что подобный подход может использоваться при анализе экономических, социологических, демографических и других данных. В частности он может использоваться для поиска новых потенциальных и свободных мест на рынках, в политическом спектре и пр.