|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Проверка простой гипотезы относительно простой альтернативы
Значимость и мощность критерия
Рассмотрим некоторый критерий 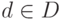 , заданный критической
областью
, заданный критической
областью 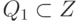 . Ошибки первого рода, порождаемые этим
критерием, соответствуют отвержению правильной нуль-гипотезы.
Следовательно, такие ошибки происходят при попадании выборочной
точки z, являющейся реализацией случайной величины
с распределением p2(z), в критическую область Q1
(см. табл. 4.3).
Вероятность таких ошибок
. Ошибки первого рода, порождаемые этим
критерием, соответствуют отвержению правильной нуль-гипотезы.
Следовательно, такие ошибки происходят при попадании выборочной
точки z, являющейся реализацией случайной величины
с распределением p2(z), в критическую область Q1
(см. табл. 4.3).
Вероятность таких ошибок
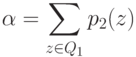 |
( 18.6) |
Ошибка второго рода соответствует выборочным точкам z, порожденным случайной величиной с распределением p1(z) и попадающим в дополнение критической области, т.е. во множество Q2 из (18.5). Поэтому вероятность таких ошибок есть
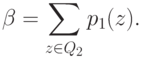 |
( 18.7) |
 |
( 18.8) |
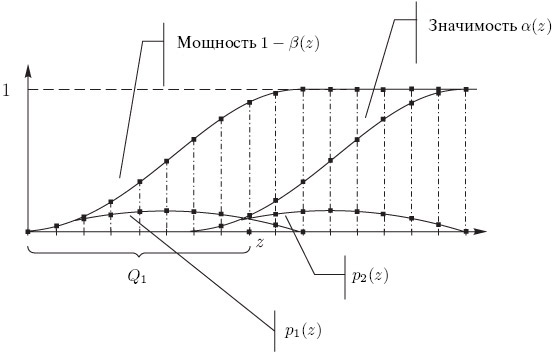
Отметим, что величины (18.06) и (18.8), характеризующие (соответственно) значимость и мощность критерия, определяются суммированием распределений p2(z) и p1(z) по одной и той же критической области Q1. Это обстоятельство ограничивает возможность формирования критической области, обеспечивающей одновременно высокую (т.е. близкую к нулевому значению) значимость критерия и высокую (т.е. близкую к единичному значению) мощность критерия.
В качестве иллюстрации на рис. 4.3 приведены функции правдоподобия p1(z), p2(z) и соответствующие им кривые мощности  и значимости
и значимости  для случая
для случая  .
Параметр z задает критическую область
.
Параметр z задает критическую область
 |
( 18.9) |