|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Интегрирование полиномов и рациональных функций. Некоторые сведения из дифференциальной алгебры. Структурная теорема
Предположим, что существует элементарная функция 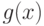 , такая,
что
, такая,
что  . По теореме Лиувилля функция
. По теореме Лиувилля функция 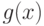 имеет
вид
имеет
вид  , где
, где 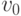 -рациональная функция от
-рациональная функция от  , коэффициенты которой
принадлежат полю
, коэффициенты которой
принадлежат полю  ,
, 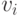 -полиномы от
-полиномы от  , которые можно считать неприводимыми, коэффициенты которых
являются
рациональными функциями от
, которые можно считать неприводимыми, коэффициенты которых
являются
рациональными функциями от  с алгебраическими (комплексными)
коэффициентами. Пользуясь свойствами логарифмов, мы можем разбить
сумму логарифмов на две части:
с алгебраическими (комплексными)
коэффициентами. Пользуясь свойствами логарифмов, мы можем разбить
сумму логарифмов на две части:
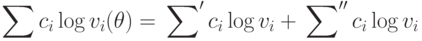
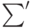 полиномы
полиномы 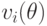 являются неприводимыми
полиномами от
являются неприводимыми
полиномами от  со старшим коэффициентом 1, а в
со старшим коэффициентом 1, а в 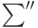 полиномы
полиномы 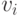 не зависят от
не зависят от  .
.Пусть  , где
, где  -полином от
-полином от  , а
, а  - правильная рациональная функция от
- правильная рациональная функция от  . При
дифференцировании по
. При
дифференцировании по  функции
функции  первое слагаемое дает регулярную часть
(полином), второе и
третье -правильные дроби от
первое слагаемое дает регулярную часть
(полином), второе и
третье -правильные дроби от  , а производная четвертого
слагаемого не зависит от
, а производная четвертого
слагаемого не зависит от  (является рациональной
функцией от
(является рациональной
функцией от  ).
Поскольку в правой части равенства
).
Поскольку в правой части равенства  стоит полином от
стоит полином от  , этот полином (с точностью до свободного
члена) должен сокращаться с
, этот полином (с точностью до свободного
члена) должен сокращаться с  .
.
Пусть  , где
, где 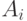 - функции,
зависящие от
- функции,
зависящие от  . Дифференцируя по
. Дифференцируя по  , получаем
, получаем
 |
( 23.3) |
Для  должны выполняться равенства
должны выполняться равенства  , откуда
, откуда  . Мы предполагали, что
. Мы предполагали, что  , а это
возможно только при
, а это
возможно только при  , поскольку функция
, поскольку функция  трансцендентна над
трансцендентна над  .
.
Для 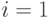 получаем уравнение
получаем уравнение
 |
( 23.4) |
 .
Предположим,
что
.
Предположим,
что  , где
, где 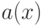 - полином, а
- полином, а 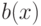 - правильная
рациональная дробь.
- правильная
рациональная дробь.Подставляя в (23.4), получаем для полиномиальной части уравнение  , которое не имеет решений в кольце полиномов
, которое не имеет решений в кольце полиномов ![\mathbb C[x]](/sites/default/files/tex_cache/ad69761f9cc540c0b26512c26db28809.png) ,
поскольку при
,
поскольку при  степень полинома в левой части равна
степень полинома в левой части равна  .
.
Таким образом, уравнение (23.3) не имеет рациональных решений, а
уравнение (23.2)
-элементарных, т. е. функция вероятности ошибки  не является элементарной.
не является элементарной.
23.16. ПРИМЕР.  .
.
Введем обозначение  . Тогда
. Тогда  . Легко видеть,
что элемент
. Легко видеть,
что элемент  трансцендентен над
трансцендентен над ![\mathbb C[x]](/sites/default/files/tex_cache/ad69761f9cc540c0b26512c26db28809.png) .
.
Предположим, что 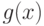 -элементарная функция. По теореме
Лиувилля она
имеет вид
-элементарная функция. По теореме
Лиувилля она
имеет вид  . Без
ограничения общности можно считать, что
. Без
ограничения общности можно считать, что ![v_i(\theta )\in \mathbb C(x)[\theta
]](/sites/default/files/tex_cache/6a614a70db707e45b8bcd81a4c506288.png) -
неприводимые полиномы от
-
неприводимые полиномы от  со старшим коэффициентом 1
или
(для одного значения
со старшим коэффициентом 1
или
(для одного значения  ) рациональная функция от
) рациональная функция от  ,
не зависящая от
,
не зависящая от  . При дифференцировании
по
. При дифференцировании
по  слагаемые вида
слагаемые вида  дают
либо правильную дробь
дают
либо правильную дробь  от
от  со
знаменателем
со
знаменателем  , либо рациональную функцию от
, либо рациональную функцию от  , если
, если 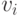 не зависит от
не зависит от  .
.
Пусть  -неприводимый делитель полинома
-неприводимый делитель полинома  . После
дифференцирования выражения
. После
дифференцирования выражения  в
знаменателе
появится полином
в
знаменателе
появится полином  , если
, если  делится на
делится на  , а числитель останется взаимно простым с
, а числитель останется взаимно простым с  .
Поскольку знаменатель правой части свободен от квадратов, отсюда вытекает,
что
.
Поскольку знаменатель правой части свободен от квадратов, отсюда вытекает,
что  .
.
Из того, что разложение правой части исходного уравнения в сумму
простейших
дробей содержит единственное слагаемое  , и предположения,
что
различные полиномы
, и предположения,
что
различные полиномы 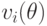 взаимно просты, следует, что от
взаимно просты, следует, что от  зависит единственное слагаемое
зависит единственное слагаемое  , т. е.
, т. е.  , где
, где  - полином. Следовательно,
- полином. Следовательно,
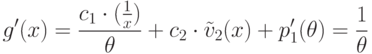
Поскольку элемент  трансцендентен над
трансцендентен над  , должно выполняться
равенство
, должно выполняться
равенство  , где
, где 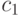 - константа,
что невозможно.
Следовательно, исходное уравнение не имеет решений в элементарных функциях.
- константа,
что невозможно.
Следовательно, исходное уравнение не имеет решений в элементарных функциях.
Алгоритм интегрирования трансцендентных функций известен как алгоритм Риша. В
его основе лежит метод неопределенных коэффициентов. Искомая функция 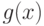 выражается в виде функции от
выражается в виде функции от 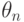 с коэффициентами из поля
с коэффициентами из поля  , и
после дифференцирования
, и
после дифференцирования 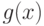 приравниваются коэффициенты при
одинаковых
степенях в левой и правой частях равенства (22.1). Найденное таким
образом
решение будет решением исходного уравнения и в том случае, если функции
приравниваются коэффициенты при
одинаковых
степенях в левой и правой частях равенства (22.1). Найденное таким
образом
решение будет решением исходного уравнения и в том случае, если функции  не являются трансцендентными, но отсутствие решения
означает
неинтегрируемость только при трансцендентных функциях
не являются трансцендентными, но отсутствие решения
означает
неинтегрируемость только при трансцендентных функциях  .
Проверка
трансцендентности элементов
.
Проверка
трансцендентности элементов  осуществляется на основе
структурной
теоремы.
осуществляется на основе
структурной
теоремы.
