НОУ ИНТУИТ | Метрология и электрорадиоизмерения. Лекция 12: Измерение фазового сдвига

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 19.01.2015 | Уровень: для всех | Доступ: платный | ВУЗ: Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики

|

Вам нравится? Нравится 78 студентам

| Поделиться |

Поддержать программу

Ключевые слова: модуль, разность, определение

Фазовый сдвиг

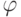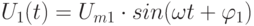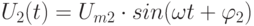Фазовым сдвигом $\varphi$ называется модуль разности начальных фаз двух гармонических сигналов одной частоты $U_{1}(t)=U_{m1}\cdot sin(\omega t+\varphi_{1})$ и $U_{2}(t)=U_{m2}\cdot sin(\omega t+\varphi_{2})$ . Таким образом фазовый сдвиг равен 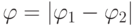$\varphi=|\varphi_{1}-\varphi_{2}|$ . Он является постоянной величиной и не зависит от момента отсчёта.

Фазовый сдвиг можно выразить через разность моментов времени 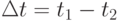$\Delta t=t_{1}-t_{2}$ , в которых эти колебания имеют одинаковые фазы (рис. 11.1 а) рис. 11.1

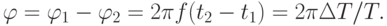$\varphi=\varphi_{1}-\varphi_{2}=2\pi f(t_{2}-t_{1})=2\pi \Delta T/T.$

( 11.1)

Это определение распространяется на два периодических сигнала несинусоидальной формы (рис.11.1 б), если в момент перехода через ноль их напряжения изменяются в одну сторону (например, от положительных значений к отрицательным).

Рис. 11.1.

Необходимость измерения фазового сдвига возникает при исследованиях фазочастотных характеристик радиотехнических устройств, измерениях реактивной мощности, оценке свойств веществ.

Приборы для измерения разности фаз называют фазометрами или измерителями фазового сдвига и согласно ГОСТ15094 подразделяются на:

Ф1 – установки и приборы для поверки измерителей фаз;
Ф2 – измерители фаз;
Ф3 – фазовращатели измерительные;
Ф4 – измерители группового времени запаздывания.

Методы измерения фазового сдвига весьма разнообразны и зависят от диапазона частот, требуемой точности и от формы исследуемых сигналов. На практике нашли применение следующие методы:

осциллографический;
компенсационный;
дискретного счета.

Осциллографический метод

Этот метод реализуется с помощью линейной, синусоидальной и круговой разверток.

Метод линейной развертки

Для этого используется двухлучевой или двухканальный осциллограф. На входы Y₁ и Y₂ подаются исследуемые сигналы. Частота развертки подбирается так, чтобы на экране наблюдалось 1-2 периода сигналов (рис.11.1 а). Измерив Т и 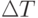$\Delta T$ по формуле 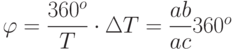$\varphi=\dfrac{360^{o}}{T}\cdot \Delta T=\dfrac{ab}{ac}360^{o}$ определяют фазовый сдвиг, где ab и ac – измеренные на экране ЭЛТ длины отрезков.

Метод синусоидальной развертки

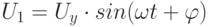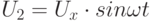Метод может быть реализован с помощью однолучевого осциллографа. Один сигнал $U_{1}=U_{y}\cdot sin(\omega t+\varphi)$ подается в канал Y, а второй $U_{2}=U_{x}\cdot sin\omega t$ – на канал Х (генератор развертки отключен). На экране осциллографа получается эллипс (рис. 11.2 рис. 11.2.), уравнение которого

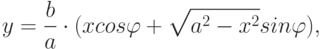$y=\dfrac{b}{a}\cdot(xcos\varphi +\sqrt{a^{2}-x^{2}}sin\varphi),$

( 11.2)

где a, b – максимальные отклонения по горизонтали и вертикали соответственно.

Рис. 11.2.

Существует ряд методов определения фазового сдвига по полученной фигуре.

Метод 1. Положив x=0 получим вертикальный отрезок 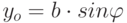$y_{o}=b\cdot sin\varphi$ . Если y=0, то горизонтальный отрезок 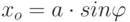$x_{o}=a\cdot sin\varphi$ . Следовательно $sin\varphi=\pm\frac{y_{o}}{b}=\pm\frac{x_{o}}{a}$ , откуда можно определить

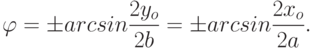$\varphi=\pm arcsin\dfrac{2y_{o}}{2b}=\pm arcsin\dfrac{2x_{o}}{2a}.$

( 11.13)

Метод неточен из-за трудности определения центра эллипса, но зато полученные формулы не зависят от соотношений U_x и U_y.

Метод 2. Реализуется при условии a=b. В этом случае $tg\varphi=l_{1}/l_{2}$ , где l₁ - малая ось эллипса, l₂ - его большая ось.

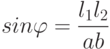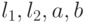Метод 3. При любых значениях a и b $sin\varphi=\dfrac{l_{1}l_{2}}{ab}$ , где $l_{1}, l_{2}, a, b$ определяются по экрану ЭЛТ осциллографа.

Осциллографический метод прост, не требует дополнительных приборов, но не даёт однозначности (знак угла) и обладает большой субъективной погрешностью. Погрешность определения фазового сдвига составляет 5-10% из-за неточностей определения длин отрезков, искажений эллипса.

Метод круговой развертки

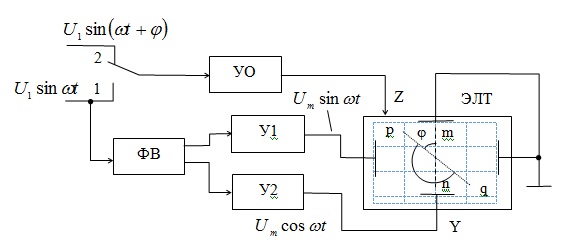
При использовании этого метода опорное напряжение с помощью фазовращателя ФВ расщепляется по фазе и в виде двух сдвинутых на 90^o напряжений подается на вход усилителей У1 и У2 каналов X и Y (рис.11.3). Регулировкой коэффициентов усиления и установлением фазовой симметрии в обоих каналах добиваются получения круговой развертки.

Рис. 11.3. Метод круговой развертки

Напряжение исследуемого сигнала подается на модулирующий электрод ЭЛТ (канал Z). На время отрицательного полупериода ЭЛТ запирается и на экране становится видимой только половина окружности. Для обеспечения необходимой точности измерений необходимо, чтобы трубка запиралась в моменты перехода сигнала через ноль, что обеспечивается применением усилителя-ограничителя УО.

В процессе измерения фазового сдвига на вход УО сначала подается опорное напряжение (положение 1) и по полуокружности на экране ЭЛТ отмечается положение диаметра mn, являющегося началом отсчета. Затем на УО подается измеряемый сигнал (положение 2) и отмечается положение pq. Измеряемый фазовый угол равен 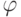$\varphi$ углу между прямыми mn и pq.

Источниками погрешности являются: непостоянство частоты круговой развертки, погрешность измерения угла между диаметрами, погрешность УО.

Дальше >>

Метрология и электрорадиоизмерения

Метрология и электрорадиоизмерения