Метрология и электрорадиоизмерения

:

Метрология и электрорадиоизмерения
[+]
Опубликован: 19.01.2015 | Уровень: для всех | Доступ: платный | ВУЗ: Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики
Лекция 4:

Нормирование погрешностей средств измерений
A
|
версия для печати
< Лекция 3 || Лекция 4 || Лекция 5 >
Аннотация: Рассмотрим подробный порядок операций, выполняемых при обработке результатов измерений. Содержание всех описываемых действий рассмотрено в предыдущих разделах. Проводимые расчеты основываются на предположении о нормальном распределении погрешностей, когда систематические погрешности уже учтены на предыдущих этапах работы с экспериментальными данными.
Ключевые слова: значение, предел, погрешность, класс, Си, точность, интервал, шкала, числитель, отношение

Нормирование погрешностей средств измерений

Нормирование метрологических характеристик средств измерений и заключается в установлении границ для отклонений реальных значений параметров средств измерений от их номинальных значений.

Каждому средству измерений приписываются некоторые номинальные характеристики. Действительные же характеристики средств измерений не совпадают с номинальными, что и определяет их погрешности.

Обычно нормирующее значение принимают равным:

  1. большему из пределов измерений, если нулевая отметка расположена на краю или вне диапазона измерения;
  2. сумме модулей пределов измерения, если нулевая отметка расположена внутри диапазона измерения;
  3. длине шкалы или её части, соответствующей диапазону измерения, если шкала существенно неравномерна (например, у омметра);
  4. номинальному значению измеряемой величины, если таковое установлено (например, у частотомера с номинальным значением 50 Гц);
  5. модулю разности пределов измерений, если принята шкала с условным нулём (например, для температуры), и т.д.

Чаще всего за нормирующее значение принимают верхний предел измерений данного средства измерений.

Отклонения параметров средств измерений от их номинальных значений, вызывающие погрешность измерений, не могут быть указаны однозначно, поэтому для них должны быть установлены предельно допускаемые значения.

Указанное нормирование является гарантией взаимозаменяемости средств измерений.

Нормирование погрешностей средств измерений заключается в установлении предела допускаемой погрешности.

Под этим пределом понимается наибольшая (без учёта знака) погрешность средства измерения, при которой оно может быть признано годным и допущено к применению.

Подход к нормированию погрешностей средств измерений заключается в следующем:

  1. в качестве норм указывают пределы допускаемых погрешностей, включающие в себя и систематические, и случайные составляющие;
  2. порознь нормируют все свойства средств измерений, влияющие на их точность.

Стандарт устанавливает ряды пределов допускаемых погрешностей. Этой же цели служит установление классов точности средств измерений.

Классы точности средств измерений

Класс точности – это обобщенная характеристика СИ, выражаемая пределами допускаемых значений его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности не является непосредственной оценкой точности измерений, выполняемых этим СИ, поскольку погрешность зависит еще от ряда факторов: метода измерений, условий измерений и т.д. Класс точности лишь позволяет судить о том, в каких пределах находится погрешность СИ данного типа. Общие положения деления средств измерений по классу точности устанавливает ГОСТ 8.401–80.

Пределы допускаемой основной погрешности, определяемые классом точности, – это интервал, в котором находится значение основной погрешности СИ.

Классы точности СИ устанавливаются в стандартах или технических условиях. Средство измерения может иметь два и более класса точности. Например, при наличии у него двух или более диапазонов измерений одной и той же физической величины ему можно присваивать два или более класса точности. Приборы, предназначенные для измерения нескольких физических величин, также могут иметь различные классы точности для каждой измеряемой величины.

Пределы допускаемых основной и дополнительной погрешностей выражают в форме приведенных, относительных или абсолютных погрешностей. Выбор формы представления зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения СИ.

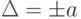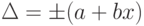Пределы допускаемой абсолютной основной погрешности устанавливаются по одной из формул: $\Delta=\pm a$ или $\Delta=\pm (a+bx)$, где x – значение измеряемой величины или число делений, отсчитанное по шкале; a, b – положительные числа, не зависящие от х. Первая формула описывает чисто аддитивную погрешность, а вторая – сумму аддитивной и мультипликативной погрешностей.

В технической документации классы точности, установленные в виде абсолютных погрешностей, обозначают, например, "Класс точности М", а на приборе – буквой "М". Для обозначения используются прописные буквы латинского алфавита или римские цифры, причём меньшие пределы погрешностей должны соответствовать буквам, находящимся ближе к началу алфавита, или меньшим цифрам. Пределы допускаемой приведенной основной погрешности определяются по формуле 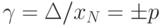$\gamma=\Delta/x_{N}=\pm p$, где xN – нормирующее значение, выраженное в тех же единицах, что и $\Delta$; p – отвлеченное положительное число, выбираемое из ряда значений:

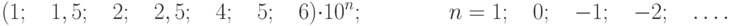
(1;\quad 1,5;\quad 2;\quad 2,5;\quad 4;\quad 5;\quad 6)\cdot10^{n};\qquad\qquad n =1;\quad 0;\quad -1;\quad - 2;\quad\ldots.

Нормирующее значение xN устанавливается равным большему из пределов измерений (или модулей) для СИ с равномерной, практически равномерной или степенной шкалой и для измерительных преобразователей, для которых нулевое значение выходного сигнала находится на краю или вне диапазона измерений. Для СИ, шкала которых имеет условный нуль, равно модулю разности пределов измерений.

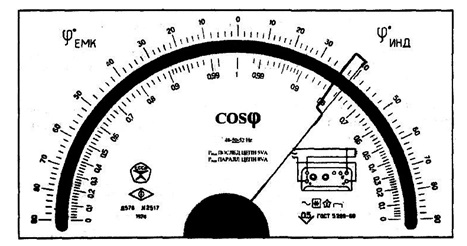
Для приборов с существенно неравномерной шкалой xN принимают равным всей длине шкалы или ее части, соответствующей диапазону измерении. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины, а на средстве измерений класс точности условно обозначают, например, в виде значка , где 0,5 – значение числа р (рис. 3.1).

Лицевая панель фазометра класса точности 0,5 с существенно неравномерной нижней шкалой

Рис. 3.1. Лицевая панель фазометра класса точности 0,5 с существенно неравномерной нижней шкалой

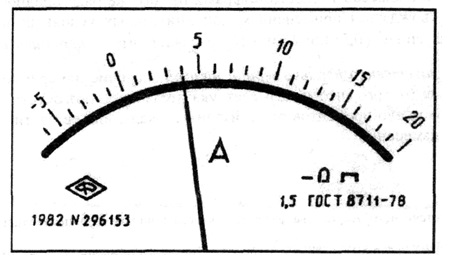
В остальных рассмотренных случаях класс точности обозначают конкретным числом р, например 1,5. Обозначение наносится на циферблат, щиток или корпус прибора (рис. 3.2).

Лицевая панель амперметра класса точности 1,5 с равномерной шкалой

Рис. 3.2. Лицевая панель амперметра класса точности 1,5 с равномерной шкалой

В том случае если абсолютная погрешность задается формулой 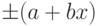$\pm (a+bx)$, пределы допускаемой относительной основной погрешности

\delta=\Delta/x=\pm[c+d(|x_{k}/x|-1)] ( 3.1)

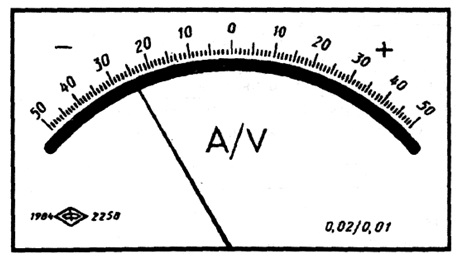
где с, d – отвлеченные положительные числа, выбираемые из ряда: 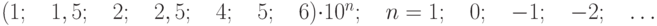$(1;\quad 1,5;\quad 2;\quad 2,5;\quad 4;\quad 5;\quad 6)\cdot10^{n};\quad n=1;\quad 0;\quad -1;\quad - 2;\quad\ldots$; – больший (по модулю) из пределов измерений. При использовании формулы 3.1 класс точности обозначается в виде "0,02/0,01", где числитель – конкретное значение числа с, знаменатель – числа d (рис. 3.3).

Лицевая панель ампервольтметра класса точности 0,02/0,01с равномерной шкалой

Рис. 3.3. Лицевая панель ампервольтметра класса точности 0,02/0,01с равномерной шкалой

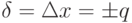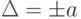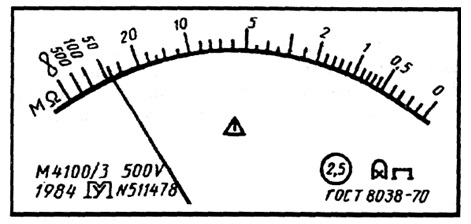
Пределы допускаемой относительной основной погрешности определяются по формуле $\delta=\Delta x=\pm q$, если $\Delta=\pm a$. Значение постоянного числа q устанавливается так же, как и значение числа p. Класс точности на прибор обозначается в виде , где 0,5 – конкретное значение q (рис. 3.4).

Лицевая панель мегаомметра класса точности 2,5 с неравномерной шкалой

Рис. 3.4. Лицевая панель мегаомметра класса точности 2,5 с неравномерной шкалой

В стандартах и технических условиях на СИ указывается минимальное значение x0, начиная с которого применим принятый способ выражения пределов допускаемой относительной погрешности. Отношение xk/x0 называется динамическим диапазоном измерения.

Правила построения и примеры обозначения классов точности в документации и на средствах измерений приведены в таблице 3.1.

Таблица 3.1. Обозначение классов точности средств измерений
Формула для определения пределов допускаемой погрешности Примеры пределов допускаемой основной погрешности Обозначение класса точности
В документах На средствах
Абсолютная погрешность
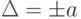$\Delta=\pm a$ $\Delta=\pm 2Гц$ Класс точности М М
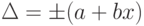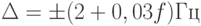$\Delta=\pm (a+bx)$ $\Delta=\pm (2+0,03f)Гц$ Класс точности С С
Приведенная погрешность
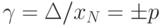$\gamma=\Delta/x_{N}=\pm p$ $\gamma=\pm 1,5\%$ Класс точности 1,5 1,5
$\gamma=\pm 0,5\%$ Класс точности 0,5 (для СИ с неравномерной шкалой)
Относительная погрешность
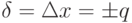$\delta=\Delta x=\pm q$ $\delta=\pm 0,5\%$ Класс точности 0,5
$\delta=\Delta/x=\pm[c+d(|x_{k}/x|-1)]$ $\delta=\Delta/x=\pm[0,02+0,01(|x_{k}/x|-1)]\%$ Класс точности 0,02/0,01 0,02/0,01

Контрольные вопросы

  1. Поясните, что такое класс точности СИ.
  2. Является ли класс точности СИ непосредственной оценкой точности измерений, выполняемых этим СИ?
  3. Перечислите основные принципы, лежащие в основе выбора нормируемых метрологических характеристик средств измерений.
  4. Как нормируются приборы по классам точности?
  5. Какие метрологические характеристики описывают погрешность средств измерений?
  6. Как осуществляется нормирование метрологических характеристик средств измерений?
Дальше >>
< Лекция 3 || Лекция 4 || Лекция 5 >

Вопросы и ответы

вопросов: 7
Александр Мантей
Александр Мантей
Входит ли данный курс в перечень программы по переподготовки ФСТЭК?
ответить
Егор Панькин
Егор Панькин

Когда планируется закончить наполнение третьего модуля прогрумы?

ответить

Студенты

всего: 215
Эльвира Белкина
Эльвира Белкина
Россия, Соликамск, Соликамский педагогический институт, 2008
предложить дружбу
Константин Алманцев
Константин Алманцев
Россия, Йошкар-ола, Поволжский государственный технологический университет, 2014
предложить дружбу