|
Непонятно почему в примере - отношение t НЕ транзитивно, ведь пары (2,4) и (4, 6) влекут (2, 6) и эта пара имеет общий делитель 2. |
Свойства отношений
Отношения эквивалентности и порядка
Определение. Бинарное отношение на множестве называют отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно .
Пример 1. На множестве всех треугольников отношение, определяемое как  , является тривиальным отношением эквивалентности.
, является тривиальным отношением эквивалентности.
Пример 2. Отношение, определяемое на множестве всех программ
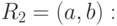
 и
и  вычисляют одну и ту же функцию на определенной машине, это является отношением эквивалентности.
вычисляют одну и ту же функцию на определенной машине, это является отношением эквивалентности.Поскольку из понятия равенства (скажем, между числами) возникает математическое понятие эквивалентности, некоторые неравенства могут также использоваться как модели для более широкого класса отношений.
Частичным порядком на множестве  назовем отношение, которое рефлексивно, антисимметрично и транзитивно. Порядок (называемый также отношением порядка) - это обобщение отношения
назовем отношение, которое рефлексивно, антисимметрично и транзитивно. Порядок (называемый также отношением порядка) - это обобщение отношения 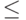 на
на  . Поэтому можно легко проверить требуемые три свойства. Заметим, что мы могли бы в качестве определения взять отношение
. Поэтому можно легко проверить требуемые три свойства. Заметим, что мы могли бы в качестве определения взять отношение  . Тогда отношение порядка было бы только транзитивно.
Следовательно, свойство транзитивности является наиболее важным для отношения порядка.
. Тогда отношение порядка было бы только транзитивно.
Следовательно, свойство транзитивности является наиболее важным для отношения порядка.
Определив отношение  можно определить отношение
можно определить отношение  следующим образом:
следующим образом: 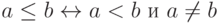 .
.
Аналогично, если задано  , то
, то  . Пример 1. Порядок чисел на действительной оси
. Пример 1. Порядок чисел на действительной оси 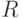 является полным.
является полным.
Пример 2 (
рис.
4.5). Отношение 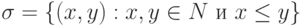 рефлексивно, антисимметрично, транзитивно.
рефлексивно, антисимметрично, транзитивно.
Функции
Подмножество 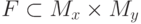 называется функцией, если для каждого элемента
называется функцией, если для каждого элемента 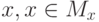 , найдется не более одного элемента
, найдется не более одного элемента  вида
вида 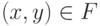 ;
;
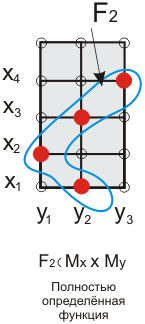
При этом если для каждого элемента  имеется один элемент
имеется один элемент  вида
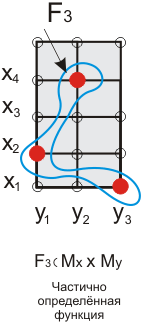
вида 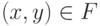 , то функция называется всюду (полностью) определенной, в противном случае - частично определенной (недоопределенной).
, то функция называется всюду (полностью) определенной, в противном случае - частично определенной (недоопределенной).
Множество 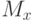 образует область определения функции
образует область определения функции  , множество
, множество 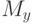 - область значения функции
- область значения функции  . Часто вместо записи
. Часто вместо записи 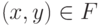 используют запись
используют запись 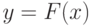 ; при этом
; при этом  называют аргументом или переменной, а
называют аргументом или переменной, а  - значением функции.
- значением функции.
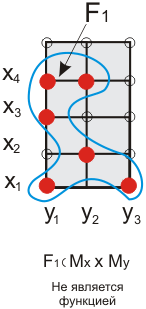
Пример. 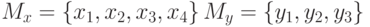 (
рис.
4.6).
(
рис.
4.6).
Функция 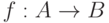 является отображением, если область ее определения совпадает с
является отображением, если область ее определения совпадает с  , т. е.
, т. е. 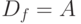 . Отображение на множество называют трансформацией (преобразованием).
. Отображение на множество называют трансформацией (преобразованием).