|
Непонятно почему в примере - отношение t НЕ транзитивно, ведь пары (2,4) и (4, 6) влекут (2, 6) и эта пара имеет общий делитель 2. |
Отношения
Графические представления отношений
Записанные в виде множества упорядоченных пар отношения иногда нелегко расшифровываются.
Отношения - это множества, обладающие определенной структурой; их элементы имеют несколько компонентов, и поэтому, в принципе, мы можем использовать диаграммы Венна для их изображения, но существуют более эффективные методы, особенно для бинарных отношений.
Координатный метод
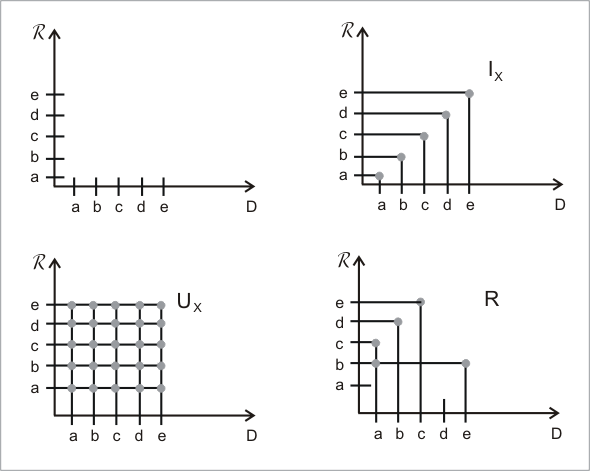
Пусть дано множество 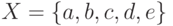 и отношения:
и отношения:
тождественное 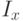 , универсальное
, универсальное 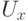 и некоторое отношение
и некоторое отношение 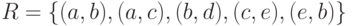 .
.
Координатный метод относится к традиционной аналитической геометрии ( рис. 3.3).
Основной недостаток этого метода заключается в том, что при увеличении мощности 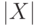 трудно увидеть элементы в области и установить соответствие с точками, обозначающими отношения.
трудно увидеть элементы в области и установить соответствие с точками, обозначающими отношения.
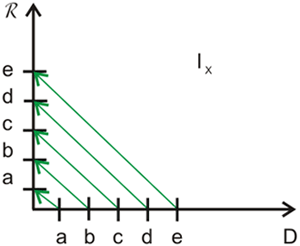
Линейно-координатный метод
Для преодоления недостатка предыдущего метода можно опустить точки и соединить стрелкой 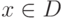 и
и 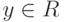 , когда
, когда 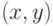 принадлежат отношению. Иллюстрация предыдущего примера линейно-координатным методом показана на
рис.
3.4.
принадлежат отношению. Иллюстрация предыдущего примера линейно-координатным методом показана на
рис.
3.4.
Диаграмма 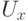 получилась довольно запутанной, зато отношения
получилась довольно запутанной, зато отношения 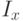 и
и 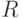 получились наглядными.
получились наглядными.
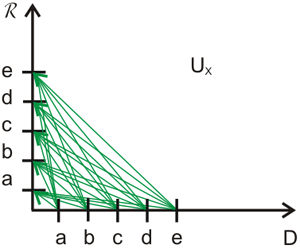
Линейный метод
Используя параллельные вертикальные линии для 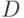 и
и 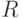 получаем диаграммы, в которых стрелки не требуются в принципе, так как мы двигаемся слева направо (
рис.
3.5).
получаем диаграммы, в которых стрелки не требуются в принципе, так как мы двигаемся слева направо (
рис.
3.5).
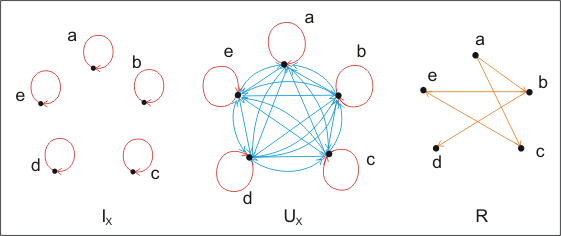
Графовый метод
Элементы множества, на котором строится отношение, представлены вершинами графа, а сами отношения - дугами графа (
рис.
3.6). Так как точки 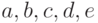 в областях
в областях 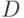 и
и 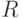 одни и те же, их можно объединить.
одни и те же, их можно объединить.