|
Непонятно почему в примере - отношение t НЕ транзитивно, ведь пары (2,4) и (4, 6) влекут (2, 6) и эта пара имеет общий делитель 2. |
Алгебра множеств
Нахождение мощности объединения множеств
-
Мощность объединения двух множеств:
 (
рис.
2.4).
(
рис.
2.4). -
Мощность объединения трех множеств:
 (
рис.
2.5).
(
рис.
2.5).Доказательство:

-
Мощность объединения
 множеств:
множеств:Теорема.
 - некоторые множества, тогда мощность объединения
- некоторые множества, тогда мощность объединения  множеств определяется по формуле
множеств определяется по формуле![\begin{array}
\left| А_1 \cup А_2 \cup .... \cup A_n | = \left| A_1 \right| + \left| A_2 \right| +...+\\
+ \left| A_n \right| - \left[ \left| А_1 \cap А_2 \right| + \left| А_1 \cap А_3 \right| + ...+ \left| A_{n-1} \cap A_n \right| \right] + \\
\left[ \left| А_1 \cap А_2 \cap А_3 \right| + \left| А_1 \cap А_2 \cap А_4 \right| + ... + \left| A_{n-2} \cap А_{n-1} \cap А_n \right| \right] -...\\
+ (-1)^{n-1} \left| А_1 \cap А_2 \cap....A_n \right| .\\
\end{array}](/sites/default/files/tex_cache/bac8852a09e893409db8a79ded1a28ca.png)
Правая часть этой формулы является суммой
 слагаемых,
слагаемых,  -е по порядку слагаемое имеет вид
-е по порядку слагаемое имеет вид  , где
, где  есть сумма чисел мощностей
есть сумма чисел мощностей  по всем возможным пересечениям k разных множеств из множеств
по всем возможным пересечениям k разных множеств из множеств 
Пример. На потоке из 100 студентов 28 человек изучают английский язык, 30 человек - немецкий язык, 42 человека - французский язык. Причем 8 человек изучают два языка - английский и немецкий, 10 человек изучает английский и французский языки, 5 человек - немецкий и французский языки. 3 человека изучают все 3 языка. Сколько студентов не изучает ни один из перечисленных языков?
Пусть
 - множество студентов,
- множество студентов,  (студентов).
(студентов).  - множество студентов, изучающих английский язык,
- множество студентов, изучающих английский язык,  ;
;  - множество студентов, изучающих немецкий язык
- множество студентов, изучающих немецкий язык  ,
,  - множество студентов, изучающих французский язык,
- множество студентов, изучающих французский язык,  .
.Соответственно множества студентов, изучающих по 2 или 3 иностранных языка заданы следующим образом:
 .
. - множество студентов, изучающих иностранные языки.
- множество студентов, изучающих иностранные языки.
 - множество студентов, не изучающих иностранный язык.
- множество студентов, не изучающих иностранный язык.
Векторы и прямые произведения
Векторы. Проекция вектора
Вектор (или кортеж) - это упорядоченный набор элементов. Например,  . Элементы вектора называются координатами или компонентами. Число координат - длина вектора (размерность).
. Элементы вектора называются координатами или компонентами. Число координат - длина вектора (размерность).
Координаты вектора могут совпадать  .
.
Два вектора равны, если они имеют одинаковую длину и равны соответствующие координаты:  и
и 

Проекцией вектора 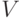 на ось
на ось  (
(  ) называется его i-я компонента.
) называется его i-я компонента. 
Проекцией вектора  на оси с номерами
на оси с номерами  называется вектор
называется вектор  длины
длины  .
.
Пример:  ,
,



Прямое произведение
Прямым (декартовым) произведением множеств  и
и  (
(  ) называется множество всех векторов
) называется множество всех векторов  , таких, что
, таких, что  :
:

Если  , то
, то  . Аналогично для нескольких множеств. Прямым произведением множества
. Аналогично для нескольких множеств. Прямым произведением множества  называется множество всех векторов длины
называется множество всех векторов длины  , таких, что
, таких, что  .
.

Примеры.
-
Множество
 - множество точек плоскости, точнее пар вида
- множество точек плоскости, точнее пар вида  , где
, где  и являются координатами.
и являются координатами. -
 .
.
-
 - множество букв, символов, знаков препинания и т. д. Тогда элементы множества
- множество букв, символов, знаков препинания и т. д. Тогда элементы множества  - слова длины
- слова длины  . Множество всех слов
. Множество всех слов  составляет язык.
составляет язык. -
 .
.Следовательно,
 .
.
Теорема о мощности прямого произведения
Пусть  - конечные множества. Соответственно мощности этих множеств равны:
- конечные множества. Соответственно мощности этих множеств равны:  .
.
Тогда мощность прямого произведения  множеств равна произведению мощностей соответствующих множеств, т.е.
множеств равна произведению мощностей соответствующих множеств, т.е.  .
.
Доказательство методом математической индукции.
Для 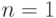 теорема тривиально верна. Предположим, что она верна и для
теорема тривиально верна. Предположим, что она верна и для 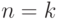 и докажем ее справедливость для
и докажем ее справедливость для  .
.
По предположению  . Возьмем любой вектор
. Возьмем любой вектор  из
из  и припишем справа элемент
и припишем справа элемент  . Это можно сделать
. Это можно сделать  способом, т. е. получим
способом, т. е. получим  различных векторов из
различных векторов из  .
.
Таким образом, из всех  векторов приписыванием справа элемента из
векторов приписыванием справа элемента из  можно получить
можно получить  векторов, причем все они различны. Поэтому для
векторов, причем все они различны. Поэтому для  теорема верна и, следовательно, верна для любых
теорема верна и, следовательно, верна для любых  .
.
Следствие: 




 -
- 