| Казахстан |
Дискретизация. Антиалиасинг. Геометрические преобразования растровых изображений
Разложение преобразований в композицию более простых
В некоторых случаях имеет смысл раскладывать сложное преобразование в последовательность более простых, для которых существуют эффективные алгоритмы.
Самый простой и полезный пример - представление общего преобразования T в виде композиции преобразований по столбцам и по строкам. Преобразования, сохраняющие столбцы или строки, можно эффективно распараллелить (по столбцам и строкам соответственно).
Пусть  , где C сохраняет столбцы, а R - строки. Пусть
, где C сохраняет столбцы, а R - строки. Пусть 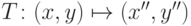 , а промежуточный результат -
, а промежуточный результат -  . Тогда
. Тогда

Отсюда получаем, что
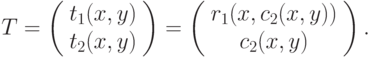
Таким образом, c2(x, y) = t2(x, y) и r1(x, t2(x, y)) = t1(x, y). Для того, чтобы найти r1, надо в выражении t1 вычленить все подвыражения, содержащие y, и привести их к виду t2(x, y). После этого, заменив эти подвыражения на y, получим выражение для r1.
Рассмотрим эту процедуру на примере поворота на угол  :
:
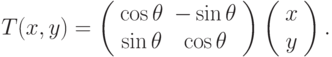
Тогда
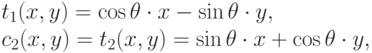
тогда  (это, конечно, возможно, когда
(это, конечно, возможно, когда  . Отсюда
. Отсюда

Получаем, что 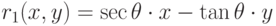 . Итак, получено следующее разложение (наглядно на рис. 7.20):
. Итак, получено следующее разложение (наглядно на рис. 7.20):
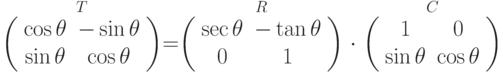
В вырожденном случае ( 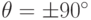 ) такое разложение не получится, но в этом случае всё T сведется к замене x на y и возможному отражению (когда
) такое разложение не получится, но в этом случае всё T сведется к замене x на y и возможному отражению (когда  ). Следует также отметить, что вращений на углы
). Следует также отметить, что вращений на углы  , близких к
, близких к  , следует избегать, т.к. при их применении произойдут слишком большие искажения по вертикали (слишком сильное сжатие). В этом случае корректнее произвести поворот сначала на
, следует избегать, т.к. при их применении произойдут слишком большие искажения по вертикали (слишком сильное сжатие). В этом случае корректнее произвести поворот сначала на  , а затем
уже на
, а затем
уже на 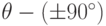 (знак соответствует близкому к
(знак соответствует близкому к  углу). Преобразования C и R представляют собой композицию сжатия и скоса по вертикали и горизонтали соответственно. Поэтому данная декомпозиция позволяет реализовать поворот с помощью нескольких последовательных применений алгоритма Веймана для скосов и масштабирования.
углу). Преобразования C и R представляют собой композицию сжатия и скоса по вертикали и горизонтали соответственно. Поэтому данная декомпозиция позволяет реализовать поворот с помощью нескольких последовательных применений алгоритма Веймана для скосов и масштабирования.
Существует альтернативное разложение на 3 скоса для матрицы поворота (наглядно на рис. 7.21), которое позволяет избавиться от существенных искажений при 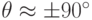 , присущих вышеизложенному алгоритму:
, присущих вышеизложенному алгоритму:

Алгоритм Веймана рекомендуется применять именно вместе с таким разложением.
7.4. Заключение
Тема дискретизации, представления и обработки изображений (англ. image processing) является самостоятельной научной дисциплиной. Более подробно с ней можно ознакомиться по книгам [44], [32], [9]. Тема геометрических преобразований подробно раскрыта в книге [52].



