Дискретизация. Антиалиасинг. Геометрические преобразования растровых изображений

Алгоритм Ву

Ву разработал альтернативный алгоритм для растеризации кривых со встроенным антиалиасингом [54]. В нем он предложил несколько другой критерий для выбора значений интенсивности пикселей.

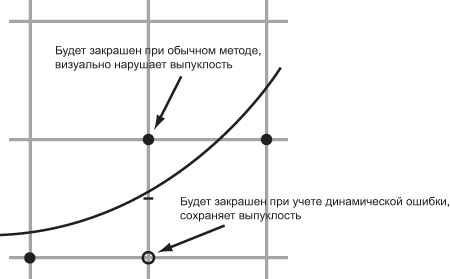
Пусть мы хотим растеризовать некоторую кривую. Без ограничения общности будем считать, что она локально наклонена горизонтально, т.е. ее можно представить как функцию y = f(x) и f'(x) < 1. При классической растеризации без антиалиасинга для каждого столбца пикселей с абсциссой i просто закрашивается ближайший к f(i) пиксель с ординатой , т.е. минимизируется ошибка |Y_i - f(i)|. В то же время Ву замечает, что при такой растеризации возможны неприятные визуальные эффекты (см. рис. 7.13), и предлагает минимизировать динамическую ошибку, возникающую при растеризации E_ij = |(f(i) - f(j)) - (Y_i - Y_j)| и показывающую насколько искажается наклон кривой. Если часть кривой соответствует абсциссам в отрезке [0, a], то предлагается минимизировать норму матрицы 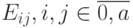, что в общем случае является вычислительно сложной задачей комбинаторной оптимизации.

Если же рассматривать возможность закрашивать пиксели с несколькими уровнями интенсивности, то можно в каждом столбце распределять исходную интенсивность в точке (i, f(i)) по двум соседним пикселям так, чтобы центр тяжести (если интенсивность рассматривать как массу) приходился на точку (i, f(i)) ; таким образом с учетом усреднения получаем E = 0. Пусть исходная интенсивность кривой равна I₀, тогда

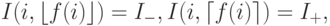
так что

Рис. 7.13. Погрешность при аппроксимации кривой.

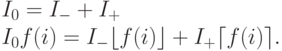
Из этой системы легко получается решение:

( 7.9)

( 7.10)

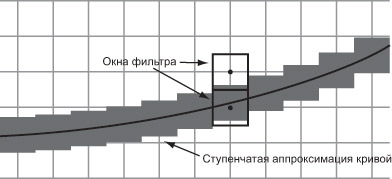
Если рассмотреть данный подход с точки зрения фильтрации, то сигнал здесь представлен объединением квадратов

и используется фильтр-параллелепипед радиуса 1/2 (см. рис. 7.14).

Рассмотрим применение данного подхода к растеризации отрезка с целочисленными координатами концов. Пусть строится отрезок . Тогда прямая определяется формулой y = kx, где k = b/a. Для максимального быстродействия будем проводить все вычисления приближенно, используя лишь целочисленную арифметику. Пусть D отвечает за дробную часть y. , где n - число разрядов в машинном представлении целых чисел. На каждом шаге будем прибавлять к D аппроксимацию k (обозначим ее d ):

Рис. 7.14. Аппроксимация кривой по Ву.

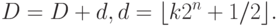
Ошибка аппроксимации e = k - d2^-n не превосходит по модулю 2^-n. D естественным образом будет содержать дробную часть f(i), умноженную на 2ⁿ, т.к. машинная арифметика автоматически осуществляет сложение по модулю 2ⁿ. Единственное, что нужно в тех случаях, когда происходит переполнение^{2Обычно процессор содержит специальный флаг, который указывает на то, произошло ли переполнение при предыдущей арифметической операции.}, увеличивать текущее значение y (которое отвечает за целую часть kx ) на 1 (т.е. диагональный сдвиг).

Пусть значения интенсивности пикселя определяются m -разрядным числом, тогда максимальное значение I₀ = 2^m-1. m, как правило, много меньше n (обычно, m = 8, n = 32 ). В соответствии с уравнениями 7.9 для столбца с абсциссой x,

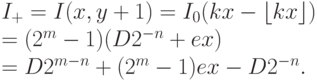
Учитывая, что I₊ должна быть целочисленной, пренебрежем последними двумя членами (в статье [54] подробно обосновывается почему ошибка будет пренебрежимо малой): I₊ = D2^n-m. Фактически это целое, полученное из m старших двоичных разрядов D. Отсюда довольно легко получить и 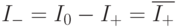( здесь означает двоичное дополнение). Это следует из того, что битовое представление 2^m - 1 - D2^m-n является двоичным дополнением D2^m-n.

Также используя оптимизацию, заключающуюся в одновременной закраске с двух концов ( "Алгоритмы растеризации отрезков, окружностей и эллипсов" ), получаем следующий алгоритм.

// Координаты концов отрезка - (0,0) и (a,b)
// plot(x,y,I) закрашивает пиксель (x,y) с интенсивностью I
// I0 - максимальная интенсивность (2^m-1)

x0 = 0; x1 = a; y0 = 0; y1 = b;
plot(x0,y0,I0);
plot(x1,y1,I0);

D = 0;
d = floor( (b/a)*2^n + 0.5 );

while( x0 < x1 )
{
      D = D + d;
      if( произошло переполнение D )
      {
            y0++; y1--;
      }

      I1 = D / 2^(n-m); // битовый сдвиг вправо на n-m
      I2 = двоичное_доп( I1 );
      plot(x0,y0,I1);
      plot(x1,y1,I1);
      plot(x0,y0+1,I2);
      plot(x1,y1-1,I2);
}

Хотя алгоритм Ву теоретически не очень качественный, т.к. использует грубую аппроксимацию кривой и грубый фильтр-параллелепипед, но на практике он успешно справляется с задачей антиалиасинга, обладая при этом большей простотой реализации (в частности, аппаратно) и скоростью, чем алгоритм Гупты-Спрулла.