| Россия, Москва, МЭИ, 2006 |
Базовые положения теории многофункциональных логических модулей
5.4. Нейроподобная модель универсальных дискретных модулей с ассоциативным управлением по "сходству" и по "отличию"
Введем и исследуем избыточную по управлению формальную модель универсальных дискретных модулей и на ее основе покажем как совместимость перечислительных схем, использующих ассоциации по "сходству" и "отличию", так и гиперкомбинаторную размерность задачи управления одним реальным нейроном.
Каноническая тройка (5.13) обобщает классическую многопороговую модель формального нейрона и исходит из условия (5.15) точной настройки на заданный класс функций (5.2), то есть предполагает фиксированными структурные параметры класса функций  .
.
Функционирование реальных нейронов предполагает не только выбор структурных параметров, но и возможность неточной настройки, как на сам класс, так и на отдельные его функции. В частности, экспериментально показано [112], что установление нового отношения "стимул - реакция" происходит только в том случае, если старое отношение того же типа обеспечивает полезный приспособительный эффект всего в 50 % инструментальных действий животного.
Условие неточной настройки на конкретную 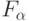 реализуемо как при точной (5.15) настройке УДМ на класс
реализуемо как при точной (5.15) настройке УДМ на класс 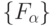 , так и при неточной (5.16) его настройке. Но в последнем, отвечающем условиям функционирования реального нейрона случае его адаптивные возможности резко возрастают.
, так и при неточной (5.16) его настройке. Но в последнем, отвечающем условиям функционирования реального нейрона случае его адаптивные возможности резко возрастают.
Определение 5.2. Произвольная функция 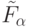 , случайно выбранная из множества функций
, случайно выбранная из множества функций 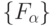 типа (5.2), аппроксимирует некоторую функцию
типа (5.2), аппроксимирует некоторую функцию  с абсолютной ошибкой
с абсолютной ошибкой  , если
, если 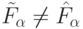 ровно на
ровно на  (любых) наборах значений ее аргументов
(
(любых) наборах значений ее аргументов
(  ).
).
Из определения 5.2 следует, что по отношению к заданной функции  все множество
все множество 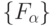 можно разбить на непересекающиеся классы (
можно разбить на непересекающиеся классы (  -эквивалентности, которое не исключает, а дополняет рассмотренное ранее отношение
-эквивалентности, которое не исключает, а дополняет рассмотренное ранее отношение 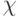 -эквивалентности.
-эквивалентности.
Аналитическую оценку мощности классов  -эквивалентности получим исходя из того, что любая
-эквивалентности получим исходя из того, что любая 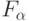 из (5.2) представляет собой упорядоченную последовательность
из (5.2) представляет собой упорядоченную последовательность 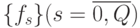 .
.
Тогда количество всех последовательностей вида (5.2), отличающихся ровно  -значениями (в любых
-значениями (в любых  -позициях) от некоторой фиксированной последовательности того же вида, будет [124]:
-позициях) от некоторой фиксированной последовательности того же вида, будет [124]:
![R[k,<q_{i} >,n,\delta] = (k-1)^{\delta}С^{\delta}_{Q+1},](/sites/default/files/tex_cache/e6b439e7e548803bd8b096c3d8612681.png) |
( 5.20) |
где  - число сочетаний из
- число сочетаний из 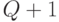 элементов по
элементов по  .
.
Из (5.20) и определения 5.2 следует, что количество классов (  -эквивалентности зависит только от мощности множества наборов значений входных аргументов, а количество функций в каждом классе определяется еще и мощностью множества допустимых значений
-эквивалентности зависит только от мощности множества наборов значений входных аргументов, а количество функций в каждом классе определяется еще и мощностью множества допустимых значений 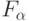 типа (5.2). Исключение составляет только ("вырожденный") класс булевых функций
(
типа (5.2). Исключение составляет только ("вырожденный") класс булевых функций
( 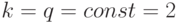 ), для которого
), для которого ![R[2,n, \delta]=C_2^{\delta}*n](/sites/default/files/tex_cache/12231aa1bd5b363386f99fecc1aa7dd5.png) , то есть количество функций каждого класса определяется биномиальным рядом, который нарушается уже при
, то есть количество функций каждого класса определяется биномиальным рядом, который нарушается уже при  (табл. 5.5).
(табл. 5.5).
 |
 |
 |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 1 | 1 | 2 | 1 | ||||||||
| 2 | 1 | 4 | 6 | 4 | 1 | |||||||
| 3 | 1 | 1 | 6 | 12 | 8 | |||||||
| 2 | 1 | 18 | 144 | 672 | 2016 | 4032 | 5376 | 4608 | 2304 | 512 |
Нетрудно увидеть, что мощность всего класса функций (5.2) выражается через (5.20)
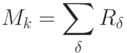 |
( 5.21) |
Перечислительный характер (5.20) и (5.21) следует из необходимости получения всех  -разбиений множества наборов значений аргументов.
-разбиений множества наборов значений аргументов.
Если в (5.9-5.11) зафиксирован только способ перечисления  , но не порядок задания
, но не порядок задания  -разбиений, то в (5.20, 5.21) не оговаривается ни первое, ни второе.
-разбиений, то в (5.20, 5.21) не оговаривается ни первое, ни второе.
Как и в случае МДМ со смешанными информационными и управляющими входами, в (5.21) за основу берется некоторая  , из которой тем или иным способом получаются подклассы
, из которой тем или иным способом получаются подклассы 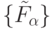 , объединение которых и дает весь класс функций типа (5.2). Отличие состоит в том, что ни на выбор "первообразной", ни на множество допустимых преобразований над ней в данном случае не накладывается никаких ограничений.
, объединение которых и дает весь класс функций типа (5.2). Отличие состоит в том, что ни на выбор "первообразной", ни на множество допустимых преобразований над ней в данном случае не накладывается никаких ограничений.
Рассматривая  типа (5.2) как упорядоченную последовательность значений
типа (5.2) как упорядоченную последовательность значений 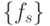 , для реализации (5.21) можно использовать алгоритм:
, для реализации (5.21) можно использовать алгоритм:
- Выполнить все подстановки
 значения
значения 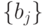 , отличного от заданного
, отличного от заданного 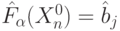 , зафиксировав значения
, зафиксировав значения  над остальными значениями
над остальными значениями  .
. - Восстановить
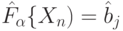 и повторить последовательно шаг 1 для остальных
и повторить последовательно шаг 1 для остальных 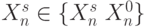 .
. - Выполнить шаги 1 и 2 над неупорядоченными двойками, тройками и так далее векторов
 до
до 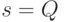 .
.
Этого алгоритма достаточно, чтобы увидеть сходство (5.21) с синтаксическими методами распознавания образов [73, 74, 125, 126], где для классификации используют минимум расстояния между эталонными  и классифицируемыми
и классифицируемыми 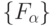 объектами. Разница состоит в том, что при распознавании образов минимизируют количество вставок, удалений и замещений
объектами. Разница состоит в том, что при распознавании образов минимизируют количество вставок, удалений и замещений 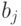 в
в  при переходе от классифицируемой
при переходе от классифицируемой 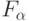 к одному из эталонов
к одному из эталонов 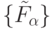 или наоборот.
или наоборот.
Таким образом, если каноническая система (5.13) обобщает перцеп-тронную модель распознавания образов [72], в которой классификация выполняется по минимуму "аналитического" или "статистического" расстояния, то при распознавании образов на основе (5.21) используется минимум "синтаксического" расстояния, измеряемого количеством подстановок символов 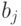 в упорядоченную последовательность
в упорядоченную последовательность 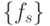 [126].
[126].
Система (5.13) использует ассоциацию по сходству управляющих воздействий, приводящих к фиксированному  -разбиению
-разбиению  на эквизначные подмножества, в то время как (5.21) базируется на ассоциации по отличию (контрасту)
на эквизначные подмножества, в то время как (5.21) базируется на ассоциации по отличию (контрасту)  -разбиений
-разбиений  , а при использовании этих преобразований в системах распознавания образов к ним добавляется третья Аристотелева ассоциация - по близости [115].
, а при использовании этих преобразований в системах распознавания образов к ним добавляется третья Аристотелева ассоциация - по близости [115].
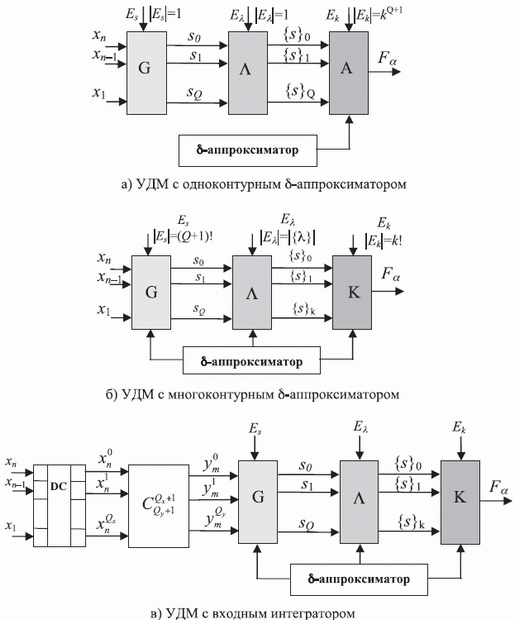
Для реализации приведенного алгоритма отображения 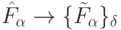 достаточно минимально избыточной модели УДМ (5.19), где вся адаптация сосредоточена в выходном контуре (рис. 5.7), реализующем размещения
достаточно минимально избыточной модели УДМ (5.19), где вся адаптация сосредоточена в выходном контуре (рис. 5.7), реализующем размещения 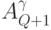 с повторениями
с повторениями 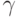 значений
значений  над одноэлементными подмножествами
над одноэлементными подмножествами 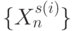 с фиксированным по
с фиксированным по 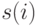 порядком их перечисления (рис. 5.9-а).
порядком их перечисления (рис. 5.9-а).
В более общем случае (рис. 5.9-б)  -аппроксиматор реализует (5.21) за счет флуктуации правил перестановки, разбиения и подстановки в канонической тройке (5.13).
-аппроксиматор реализует (5.21) за счет флуктуации правил перестановки, разбиения и подстановки в канонической тройке (5.13).
В этом случае настройка (5.13) на заданную  выполняется векторами
выполняется векторами 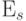 ,
, 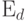 ,
, 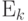 , а отображение
, а отображение 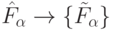 -
модификацией правила
-
модификацией правила  -аппроксимации.
-аппроксимации.
Таким образом, в схеме УДМ рис. 5.9-а и 5.9-б используется и основанный на 1-разбиениях механизм структурно-функциональной адаптации типа (5.13), и основанный на  -разбиениях флуктуационный механизм адаптации типа (5.21).
-разбиениях флуктуационный механизм адаптации типа (5.21).
Минимальная абсолютная избыточность по управлению УДМ рис. 5.9-б по отношению к УДМ рис. 5.7
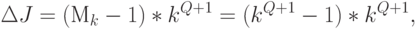 |
( 5.22) |
что для технических систем является непозволительной роскошью, которую устраняют еще на этапе синтеза средств управления.
В реальных нейронах схемы адаптации (5.13) и (5.21) по объективным причинам сосуществуют [127], и поэтому УДМ рис. 5.9-б можно рассматривать как абстрактный нейрон, для которого выражения (5.11) и (5.13) имеют вид:
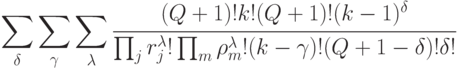 |
( 5.23) |
![[(K*G^2):( \Lambda*G_{\delta}*\Omega)]*P_{k-1}^{\delta}](/sites/default/files/tex_cache/8f85fdfda4bfcc18e6e90b29edc95142.png) |
( 5.24) |
где  - прямое произведение групп
- прямое произведение групп 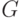 мощности
мощности 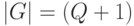 !;
!;
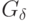 - группа перестановок мощности
- группа перестановок мощности 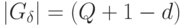 !;
!;
 - группа перестановок мощности
- группа перестановок мощности 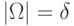 !;
!;
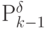 - декартово
- декартово  -произведение, заданное на входном алфавите
-произведение, заданное на входном алфавите  (с исключением
(с исключением 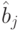 );
);
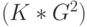 и
и 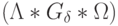 - прямое произведение соответствующих групп.
- прямое произведение соответствующих групп.
Соотношения (5.23) и (5.24) следуют из независимого использования и полноты каждого из механизмов (5.13) и (5.21).
В реальных нейронах могут сосуществовать не только разнотипные схемы адаптации, но и разные по биофизической и биохимической природе механизмы реализации одних и тех же формально-логических преобразований, что создает еще один невоспроизводимый в микроэлектронике тип функциональной избыточности.
В частности, на постсинаптической мембране реальных нейронов благодаря наличию "индифферентных" наборов значений входных переменных (мощности  !) имеется принципиальная возможность произвольного размещения "активных" наборов значений входных переменных
!) имеется принципиальная возможность произвольного размещения "активных" наборов значений входных переменных  на допустимом (морфологическом) множестве наборов
на допустимом (морфологическом) множестве наборов 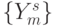 , где
, где 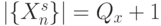 ;
;  ;
; 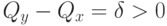 .
.
Тогда постсинаптический интерпретатор наборов значений входных переменных (рис. 5.9-в) дублирует одно из преобразований  -аппроксиматора, так как
-аппроксиматора, так как
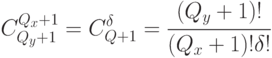 |
( 5.25) |
С учетом (5.25) для УДМ рис. 5.9-в выражения (5.23) и (5.24) принимают вид:
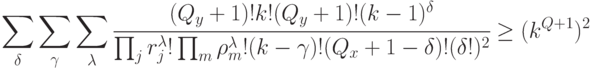 |
( 5.26) |
![[(K*G^2_y):( \Lambda*G_{x}*\Omega^2)]*P_{k-1}^{\delta}](/sites/default/files/tex_cache/464b0d3fa4249974fc053a637a10af16.png) |
( 5.27) |
Если функционирование реальных нейронов ограничить булевым алфавитом
( 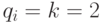 ), то и в этом случае из-за большого количества его входов (
), то и в этом случае из-за большого количества его входов ( 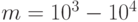 ) в левой части (5.26) получаются гиперкомбинаторные цифры. Они подтверждают хорошо известные нейрофизиологические данные [25, 128] о роли и месте механизмов эволюции, роста и развития организмов, "управляющего" влияния мотивации, обстановки, опыта и внутреннего состояния организма, влияние которых приводит к более или менее однозначному поведению нейрона (в смысле отображения состояния его входов в выходную реакцию).
) в левой части (5.26) получаются гиперкомбинаторные цифры. Они подтверждают хорошо известные нейрофизиологические данные [25, 128] о роли и месте механизмов эволюции, роста и развития организмов, "управляющего" влияния мотивации, обстановки, опыта и внутреннего состояния организма, влияние которых приводит к более или менее однозначному поведению нейрона (в смысле отображения состояния его входов в выходную реакцию).
Таким образом, введя в каноническую систему (5.13) преобразований УДМ только два типа нейроизбыточности (по управлению и по реализации преобразований), удалось показать:
- Функционирование и адаптация реальных нейронов, а тем более нейронных ансамблей, осуществляется на основе колоссальной избыточности по управлению, которая не достижима методами и средствами одной микроэлектроники даже с учетом перспектив ее развития.
- В реальных нейронах зафиксировать
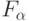 или полностью устранить неоднозначность в отображении "вход-выход", задав вектор управления в (5.24), гораздо "сложнее", чем реализовать это отображение, так как здесь мощность пространства состояний управляющих (перечисляющих) векторов гораздо больше мощности множества реализуемых (вычисляемых) функций.
или полностью устранить неоднозначность в отображении "вход-выход", задав вектор управления в (5.24), гораздо "сложнее", чем реализовать это отображение, так как здесь мощность пространства состояний управляющих (перечисляющих) векторов гораздо больше мощности множества реализуемых (вычисляемых) функций. - Функционирование систем распознавания образов синтаксического типа базируется на флуктуационных механизмах "перечисления" реали-зуемых ими отображений "вход-выход", а систем распознавания классического (статистического типа) - на структурно-функциональных механизмах, причем в первых фактически используется ассоциация по "отличию", а во вторых - "по сходству", но само распознавание выполняется по "близости", определяемой минимумом некоторого расстояния.
- Флуктуационные и структурно-функциональные механизмы адаптации МДМ совместны по используемым преобразованиям, изменяя в них только тип ассоциативного перечисления отображений "вход-выход".