| Россия, Москва, МЭИ, 2006 |
Базовые положения теории многофункциональных логических модулей
5.2. Каноническая система преобразований универсальных дискретных модулей
Из приведенных выше данных видно: для полного описания работы МПЭ требуется формальная модель, которая включает некоторую процедуру перечисления либо всех функций из фиксированного класса  - универсальный дискретный модуль (УДМ)), либо только из некоторого подкласса (
- универсальный дискретный модуль (УДМ)), либо только из некоторого подкласса ( 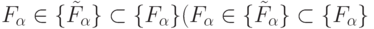 - многофункциональный дискретный модуль (МДМ)). В любом случае исходным для такого перечисления является класс или множество функций и задаваемые ими отношения эквивалентности. Поэтому раскроем роль и место преобразований, сохраняющих отношение в классах произвольнозначных логических и дискретных функций, заданных (5.2).
- многофункциональный дискретный модуль (МДМ)). В любом случае исходным для такого перечисления является класс или множество функций и задаваемые ими отношения эквивалентности. Поэтому раскроем роль и место преобразований, сохраняющих отношение в классах произвольнозначных логических и дискретных функций, заданных (5.2).
Определение 5.1. Подмножество 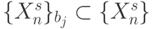 наборов значений аргументов функции
наборов значений аргументов функции 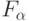 называется эквизначным, если функция принимает на нем одно и то же значение
называется эквизначным, если функция принимает на нем одно и то же значение 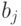 :
: 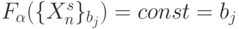
Например, двузначная ЛФ двух переменных 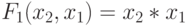 принимает значение "ноль" на наборах
принимает значение "ноль" на наборах 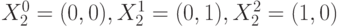 и значение "единица" на наборе
и значение "единица" на наборе 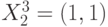 , то есть ЛФ "И" разбивает все векторное пространство
, то есть ЛФ "И" разбивает все векторное пространство 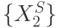 на два подмножества
на два подмножества 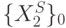 и
и 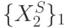 мощности
мощности 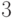 и
и  соответственно.
соответственно.
Для произвольных 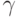 -значных функций (
-значных функций ( 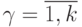 ) число эквизначных подмножеств равно
) число эквизначных подмножеств равно 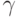 .
.
Обозначим через 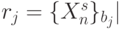 мощность
мощность 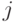 -го эквизначного подмножества
(
-го эквизначного подмножества
( 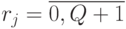 ;
; 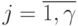 ;
; 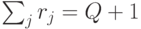 ).
).
Из определения 5.1 и (5.2) следует, что каждый вектор 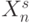 принадлежит только одному "эквизначному" подмножеству и поэтому отношение эквизначности является отношением эквивалентности, так как оно разбивает все множество
принадлежит только одному "эквизначному" подмножеству и поэтому отношение эквизначности является отношением эквивалентности, так как оно разбивает все множество  на непересекающиеся подмножества
на непересекающиеся подмножества 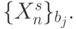
Справедливо утверждение 5.2: функция 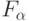 и задаваемое ею отношение
и задаваемое ею отношение 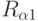 эквизначности на множестве входных векторов
эквизначности на множестве входных векторов  инвариантны перестановкам
инвариантны перестановкам 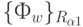 элементов внутри эквизначных подмножеств.
элементов внутри эквизначных подмножеств.
Следствие 5.1. Функция 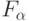 инвариантна множеству перестановок мощности:
инвариантна множеству перестановок мощности:
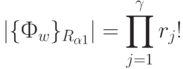 |
( 5.5) |
Для простоты будем считать, что преобразования 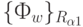 определены на множестве индексов
определены на множестве индексов 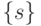 , а
, а  -разбиения на эквизначные подмножества формируются вектором порогов
-разбиения на эквизначные подмножества формируются вектором порогов 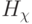 с целочисленными компонентами
с целочисленными компонентами 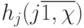 заданными на
заданными на 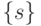 .
.
Из определения 5.1 и (5.2) следует утверждение 5.3: отношение эквизначности, задаваемое фиксированным разбиением  , инвариантно подмножеству функций
, инвариантно подмножеству функций 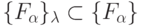 , отличающихся только порядком размещения своих у значений над эквизначными подмножествами этого разбиения.
, отличающихся только порядком размещения своих у значений над эквизначными подмножествами этого разбиения.
Следствие 5.2.1-разбиение заданной функции 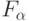 инвариантно множеству функций
инвариантно множеству функций 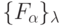 мощности:
мощности:
 |
( 5.6) |
где 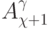 - размещения (возможно с повторениями)
- размещения (возможно с повторениями) 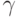 значений
значений 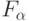 над
над  эквизначным множеством.
эквизначным множеством.
Утверждения 5.2 и 5.3 говорят о том, что эквизначные подмножества  в одном и том же разбиении
в одном и том же разбиении  можно рассматривать как неупорядоченное множество неупорядоченных подмножеств, отличающихся только количеством
можно рассматривать как неупорядоченное множество неупорядоченных подмножеств, отличающихся только количеством 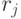 элементов в каждом.
элементов в каждом.
Отсюда следует утверждение 5.4: фиксированное отношение эквизначности инвариантно перестановкам собственных равномощных подмножеств.
Обозначим через 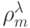 мощность множества эквизначных подмножеств, имеющих в фиксированном
мощность множества эквизначных подмножеств, имеющих в фиксированном  -разбиении одну и ту же мощность
-разбиении одну и ту же мощность
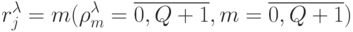
Следствие 5.3. Отношение эквизначности инвариантно множеству перестановок 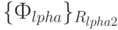 собственных равномощных подмножеств, мощность которого:
собственных равномощных подмножеств, мощность которого:
 |
( 5.7) |
В комбинаторике [90] числа 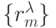 и
и 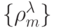 называют соответственно первичной и вторичной спецификациями, характеризующими с количественной стороны фиксированное
называют соответственно первичной и вторичной спецификациями, характеризующими с количественной стороны фиксированное  - разбиение. Чтобы учесть качественные отличия
- разбиение. Чтобы учесть качественные отличия  -разбиений с одной и той же первичной и вторичной спецификациями, необходимо отличать эквизначные подмножества по составу входящих в них элементов.
-разбиений с одной и той же первичной и вторичной спецификациями, необходимо отличать эквизначные подмножества по составу входящих в них элементов.
Введем множество 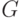 всевозможных перестановок векторов
всевозможных перестановок векторов 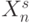 по индексу
по индексу  , такое, что мощность
, такое, что мощность 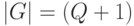 !. Тогда мощность
!. Тогда мощность 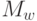 множества
множества  -разбиений, отличающихся только составом элементов в соответствии с (5.5 2.11) и (5.7 2.13) будет:
-разбиений, отличающихся только составом элементов в соответствии с (5.5 2.11) и (5.7 2.13) будет:
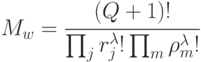 |
( 5.8) |
С учетом (5.6 2.12) мощность только 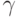 -значных функций
-значных функций 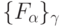 (из класса
(из класса  -значных), инвариантных фиксированному
-значных), инвариантных фиксированному  -разбиению, будет:
-разбиению, будет:
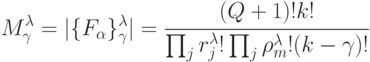 |
( 5.9) |
где вектор порогов  всегда имеет минимальную размерность
всегда имеет минимальную размерность 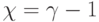 .
.
Мощность всего 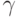 -значного (под)класса функций:
-значного (под)класса функций:
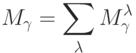 |
( 5.10) |
где суммирование ведется по всем допустимым  -разбиениям.
-разбиениям.
Мощность всего  -значного класса функций:
-значного класса функций:
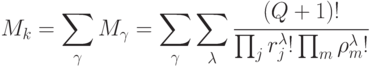 |
( 5.11) |
где суммирование ведется по всем минимально пороговым  -разбиениям числа
-разбиениям числа 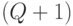 , удовлетворяющим условию
, удовлетворяющим условию 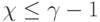 .
.
В таблицах 5.1, 5.2 приведены примеры расчета мощностей соответствующих (5.8)-(5.11) подклассов функций 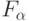 . При анализе этих таблиц следует помнить:
. При анализе этих таблиц следует помнить:  - мощность множества неупорядоченных подмножеств. С этих позиций разбиения со спецификациями
- мощность множества неупорядоченных подмножеств. С этих позиций разбиения со спецификациями 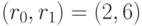 и
и 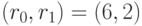 являются эквивалентными, и поэтому при определении мощности соответствующего подкласса учитывается только одно из них (см. табл. 5.2).
являются эквивалентными, и поэтому при определении мощности соответствующего подкласса учитывается только одно из них (см. табл. 5.2).
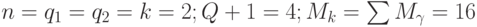 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
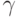 |
 |
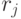 |
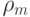 |
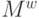 |
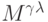 |
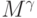 |
||||
 |
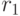 |
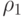 |
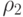 |
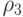 |
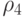 |
|||||
| 1 | 1 | 0 | 4 | 0 | 0 | 0 | 1 | 4!/4!=1 | 1*21=2 | 2 |
| 2 | 2 | 1 | 3 | 1 | 0 | 1 | 0 | 4!/1!3!=4 | 4*2!=8 | 14 |
| 3 | 2 | 2 | 0 | 2 | 0 | 0 | 4!/2!2!2!=3 | 3*2!=6 | ||
| ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
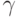 |
 |
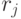 |
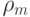 |
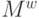 |
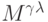 |
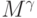 |
||||||||
 |
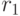 |
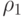 |
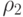 |
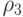 |
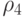 |
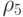 |
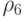 |
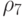 |
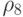 |
|||||
| 1 | 1 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 8!/0!8!=1 | 1*2!=2 | 2 |
| 2 | 2 | 1 | 7 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 8!/1!7!=8 | 8*2!=16 | 254 |
| 3 | 2 | 6 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 8!/2!6!=28 | 28*21=56 | ||
| 4 | 3 | 5 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 8!/3!5!=56 | 56*21=112 | ||
| 5 | 4 | 4 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 8!/4!4!2!=35 | 35*21=70 | ||
При построении (5.11) фактически использовано три оператора:
-
перестановок входных векторов, мощность которого:
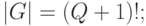
( 5.12-a) -
разбиений упорядоченного множества векторов
 на эквизначные подмножества, мощность которого:
на эквизначные подмножества, мощность которого: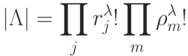
( 5.12-б) -
размещений
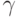 -значных функций (с выбором из
-значных функций (с выбором из  возможных) над эквизначными подмножествами, мощность которого:
возможных) над эквизначными подмножествами, мощность которого: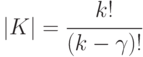
( 5.12-в)
Именно оператор  позволяет рассматривать
позволяет рассматривать  -разбиения как неупорядоченное множество неупорядоченных подмножеств, так как при любом порядке перечисления эквизначных подмножеств в фиксированном
-разбиения как неупорядоченное множество неупорядоченных подмножеств, так как при любом порядке перечисления эквизначных подмножеств в фиксированном  -разбиении всегда найдется порядок размещения
-разбиении всегда найдется порядок размещения 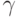 значений функции, отвечающий заданному отображению
значений функции, отвечающий заданному отображению 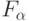 :
:  .
.
Таким образом, используя преобразования, сохраняющие отношение эквизначности, удалось показать:
- Комбинаторное соотношение (5.11) обеспечивает перечисление классов функций (5.2), причем перечислительный (а не вычислительный [118]) характер (5.11) и отвечающих ему преобразований следует из того, что в них входит индекс разбиения
 .
. -
Устойчивость реализации функций типа (5.2) вообще и динамическая устойчивость в частности обеспечивается флуктуацией или блужданием "рабочей точки" по множеству перестановок входных векторов, сохраняющих отношение эквизначности, причем мощность "рабочей области" равна
 .
. - Напротив, адаптация МДМ на одну из функций типа (5.2) связана с перечислением соответствующих параметров в операторах
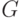 ,
,  ,
,  , изменяющих отношение эквизначности.
, изменяющих отношение эквизначности. - Полученные комбинаторные соотношения позволяют ввести формальную модель работы и настройки универсальных дискретных модулей (УДМ), которая базируется не на операциях булевой алгебры, а на общих теоретико-групповых преобразованиях.
Принятая в работе форма задания функции (5.2) идентична форме задания дискретных объектов в комбинаторике [90], и поэтому процесс адаптации УДМ, состоящий в переходе от одной функции к другой, оказывается идентичен процессу перечисления дискретных объектов,
который исследуется в рамках самостоятельной теории перечислимости Дж. Пойя [118].
В вычислительной технике перечисляемыми являются инструкции реализуемой программы, что и составляет основу управления ходом вычислительного процесса. С учетом наличия в программе операторов циклов, завершаемых по условию, а также операторов условных переходов реально реализуемый в ОКОД- или ОКМД-архитектурах поток инструкций частично упорядочен во времени, а в МКМД-архитектурах процессе - и в пространстве.
Таким образом, любой вычислительный процесс фактически состоит из двух подпроцессов: собственно вычисления, в рамках которого выполняются арифметико-логические преобразования операндов, и перечисления частных подготовительных и исполнительных инструкций, через которые выполняются требуемые преобразования данных.
Перечислительный процесс типа (5.11) исходит из общей комбинаторной схемы [90], преобразования которой можно представить [119]:
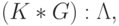 |
( 5.13) |
где:
-
 ,
, 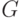 ,
,  - определенные в (5.12) соответственно группы подстановок значений реализуемой функции над эквизначными подмножествами и перестановок входных векторов и их разбиения на эквизначные подмножества;
- определенные в (5.12) соответственно группы подстановок значений реализуемой функции над эквизначными подмножествами и перестановок входных векторов и их разбиения на эквизначные подмножества; -
 - (полу)прямое произведение группы
- (полу)прямое произведение группы  и
и 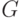 ;
; -
 - подгруппа "эквизначности", заданная на (полу)прямом произведении
- подгруппа "эквизначности", заданная на (полу)прямом произведении  с порядком
с порядком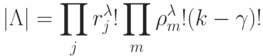
-
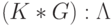 - разложение (полу)прямого произведения групп
- разложение (полу)прямого произведения групп  и
и 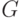 по факторгруппе "эквизначности"
по факторгруппе "эквизначности"  [119].
[119].
Если общая комбинаторная схема исследует классы дискретных объектов с количественной стороны и в предположении, что отношение эквивалентности на множестве объектов задается произвольным образом, то система преобразований (5.13) интересует нас с качественной стороны и в предположении, что отношение эквивалентности задается функциями (5.2).
Из (5.13) видно, что система преобразований, перечисляющая все 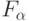 из
из 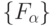 , основана на преобразованиях конечной симметрической группы [103, 120, 121] (группы подстановок), которые выполняются в следующем порядке:
, основана на преобразованиях конечной симметрической группы [103, 120, 121] (группы подстановок), которые выполняются в следующем порядке:
- вначале реализуется (полу)прямое произведение
 , учитывающее всевозможные способы упорядочения
, учитывающее всевозможные способы упорядочения  и
и 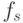 в двойках
в двойках 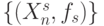 ;
; - затем с помощью факторгруппы
 из множества полученных таким образом пар
из множества полученных таким образом пар 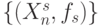 устраняются все эквивалентные отображения
устраняются все эквивалентные отображения 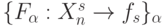 , отвечающие заданной
, отвечающие заданной 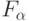 .
.
Поэтому (5.13) описывает процесс реализации заданной функции 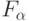 , если вариации параметров
, если вариации параметров 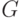 ,
,  ,
,  не нарушают заданное этой функцией отношение "эквизначности". В противном случае (5.13) описывает процесс адаптации УДМ, в результате чего происходит выбор, а значит, и последовательное перечисление
не нарушают заданное этой функцией отношение "эквизначности". В противном случае (5.13) описывает процесс адаптации УДМ, в результате чего происходит выбор, а значит, и последовательное перечисление 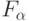 из заданного класса.
из заданного класса.
Физическому порядку выполнения преобразований (5.13) обычно отвечает последовательность "перестановки - разбиения - подстановки":
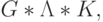 |
( 5.14) |
где входные ( 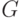 ), внутренние (
), внутренние (  ) и выходные (
) и выходные (  ) преобразования отвечают теоретико-групповым соотношениям (5.13), возможно, с некоторыми ограничениями, как это имеет место в МПЭ [79, 80].
) преобразования отвечают теоретико-групповым соотношениям (5.13), возможно, с некоторыми ограничениями, как это имеет место в МПЭ [79, 80].
Параметры преобразований (5.13) и (5.14) зависят только от классов "перечисляемых" функций и не зависят от особенностей работы и/или настройки реализующих эти преобразования УДМ. Это позволяет рассматривать (5.13) и (5.14) как каноническую тройку, задающую систему преобразований абстрактного УДМ, с помощью которого можно описать работу и настройку любого реального МДМ или УДМ.

