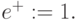Теория вычислений и машины Тьюринга

Теперь понятие алгоритма можно отождествить с машиной Тьюринга, работа которой удовлетворяет требованиям 1-8.

Согласно требованию 7 длина слов конечна, но неограниченна, а для этого требуется разделенная на отдельные ячейки счетная лента неограниченной длины, на которую можно записать как входные, так и выходные слова. Удовлетворить данное требование можно с помощью ограниченной справа, но неограниченной слева разделенной на ячейки ленты. При этом будем считать, что в одну ячейку можно записать не более одного символа, что не принципиально и создает только однозначность восприятия и исполнения предписания алгоритма (требование 4).

Согласно требованию 1 записи должны иметься только в конечном числе ячеек, то есть в подавляющем числе ячеек содержится символ "пусто" ( ).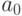

Согласно требованию 3 выполнение алгоритма носит последовательный, поэтапный характер и, если оно не обрывается, всегда ведет от одного состояния к другому. Предписание для алгоритма содержит как общие правила, определяющие сами действия над символами, способы выделения результата вычислений и т. д., так и указания, регламентирующие правила перехода от одного состояния к другому, следующему непосредственно за ним. Согласно требованиям 4 и 5 такой переход должен быть определен однозначно. При этом каждое указание требует от вычислителя определенного образа действий типа "изменить содержимое отдельной ячейки ленты", "найти другую ячейку ленты", "прекратить вычисления" и т. п. Действие "найти другую ячейку ленты" можно ограничить действием "найти соседнюю ячейку ленты", то есть машина Тьюринга может работать без перескоков и после выполнения предписания всегда смещаться на соседнюю ячейку, если не выработано условие останова вычислений.

Ячейку, с которой оперирует вычислитель, обычно называют текущей рабочей ячейкой, и предписание можно составить таким образом, чтобы изменение записи всегда происходило только в рабочей ячейке.

Отсюда, в любом состоянии предписание может состоять в следующем: "изменить содержимое рабочей ячейки", "сдвинуть рабочую ячейку вправо, а если возможно, то и влево", "остановиться".

Согласно требованиям 4-6 порядок этих действий должен быть однозначным и полностью ясным, а если процесс вычислений не остановлен, указание должно точно и однозначно предписывать, к какому непосредственно следующему указанию следует перейти после выполнения предыдущего.

Согласно требованию 6 для оценки текущего состояния, которое предваряет выполнение некоторого указания, можно привлечь только текущую запись на тенте, текущую рабочую ячейку и историю проведения вычислений.

Согласно требованию 8 у вычислителя может быть только ограниченная память. Поэтому в оценке его состояния может принять участие только ограниченная (содержательная) часть записей на ленте. Но просмотр записи из не более ячеек можно осуществить в виде 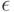-кратного просмотра содержимого только одной ячейки и за один раз. Поэтому для оценки текущего состояния вычислителя достаточно содержимого единственной ячейки, которую можно считать текущей информационной ячейкой. В свою очередь, рабочую и информационные ячейки можно совместить в одной, так как предписание всегда можно составить таким образом, чтобы сначала рабочая ячейка сменялась информационной, а затем на основе анализа содержимого последней разыскивалась исходная рабочая ячейка и определялся требуемый порядок действий (в современной терминологии "косвенная адресация").

Таким образом, для получения исполняемого указания оценку состояния вычислителя можно осуществить, используя только рабочую ячейку, ее содержимое и (пред)историю хода вычислительного процесса, от которой также можно избавиться, изменив предписание.

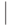Для наглядности введенных соглашений рассмотрим пример. Пусть рабочий алфавит содержит два символа: и , предписание содержит 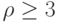указаний вида:

1. Если рабочая ячейка содержит символ , остановись. Если рабочая ячейка содержит 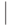, замени его символом и далее действуй согласно второму указанию.
2. Если рабочая ячейка содержит символ , замени его символом 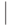в том случае, когда предыдущее действие выполнялось согласно первому указанию, и действуй далее согласно третьему указанию; в противном случае остановись. Если рабочая ячейка содержит символ 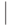, остановись.

Выделенную курсивом ссылку на предыдущее указание можно устранить следующим образом:

1. Если рабочая ячейка содержит символ , замени его символом 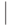и действуй согласно третьему указанию.
2. Если рабочая ячейка содержит символ 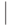, остановись.

Введем состояние. (Здесь вновь не арифметическое действие, а следующий за символ). Тогда:

1. Если рабочая ячейка содержит символ *, остановись. Если рабочая ячейка содержит 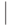, замени его символом и далее действуй согласно указанию.
2. Если рабочая ячейка содержит символ , остановись. Если рабочая ячейка содержит символ 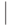, остановись. Модифицированное предписание по своему действию совпадает с исходным, но не содержит ссылок на (пред)историю.

В результате отпадает необходимость в явном виде выражать влияние прошлого в вычислительного процесса на его будущее. Для этого достаточно воспользоваться указанием на положение исполняемого в данный момент предписания во всем списке предписаний, реализуемых данным вычислителем.

Таким образом, имеются достаточные основания утверждать, что каждому алгоритму можно поставить в соответствие экстенсионально эквивалентный ему алгоритм, работающий с символами на "бесконечной" ленте по следующим общим правилам.

Рабочее состояние алгоритма в каждый момент его работы определяется текущей рабочей ячейкой и ее содержимым в тот же момент времени. Состояние вычислительного процесса вплоть до данного момента времени полностью определяется текущей рабочей ячейкой, текущим содержимым всей ленты и тем указанием или его номером в заранее оговоренном списке указаний, согласно которому выполняется текущее вычисление. Выбор текущего действия полностью и однозначно определяется содержимым текущей рабочей ячейки. Для реализации любого алгоритма требуется всего три типа действий: изменение содержимого рабочей ячейки; сдвиг рабочей ячейки на одну ячейку вправо или, если возможно, то и влево; останов. Первые два действия содержат также указание, определяющее, к какому следующему указанию надо перейти.

Алгоритмы, указания которых отвечают требованиям такой стандартной формы представления, можно промоделировать на машинах Тьюринга, так как в каждом конкретном случае введение в них предписаний общего характера фактически приводит к адекватному уточнению понятия "алгоритм".

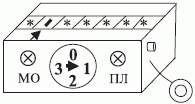
"Базовый комплект" машины Тьюринга содержит (рис. 3.1):

• операционное устройство, которое может находиться в одном из дискретных состояний, принадлежащих некоторой конечной совокупности ;
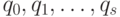• комбинированную читающую и пишущую головку;
• счетную ленту, обладающую описанными выше свойствами;
• лентопротяжный механизм, который способен сдвигать находящуюся под головкой текущую рабочую ячейку на одну ячейку вправо или, если это возможно, то и влево (на рис. 3.1 механизм не показан).

Начальным состоянием является , а ячейки ленты считаются пронумерованными начиная с левого края числами 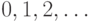Читающая и пишущая головка способна выполнять действия (считывать, стирать и записывать) над рабочим алфавитом 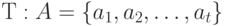и буквой 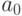, которая символизирует "пусто". Каждая ячейка ленты в каждый момент времени содержит букву из множества 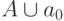, причем почти все ячейки заняты буквой

Рис. 3.1. Конструкция машины Тьюринга (без лентопротяжного механизма)

Лампочка МО зажигается при выполнении указания "машинный останов", а лампочка ПЛ - в случае когда начальная ячейка ленты находится под считывающей головкой, а затребованное действие состоит в сдвиге рабочей ячейки влево (сигнал "переход за край ленты").

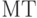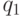Рассмотрим конкретный пример работы простейшей , оперирующей с рабочим алфавитом , символом "пусто" вида и тремя рабочими состояниями , и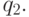

Пусть 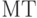работает следующим образом [45]:

1. В состоянии 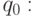вне зависимости от содержимого рабочей ячейки ( или 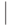) сдвигает рабочую ячейку вправо и переходит в состояние
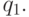
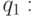
2. В состоянии заменяет стоящий в ячейке символ на 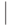, то есть выполняет подстановку вида 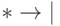или 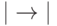, и переходит в состояние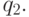
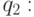
3. В состоянии останавливается вне зависимости от содержимого рабочей ячейки.

, работающая согласно приведенному предписанию, фактически делает следующее. После установки головки над некоторой ячейкой ленты (состояние ) сдвигает рабочую ячейку вправо, стирает содержимое этой ячейки, заносит в нее символ 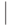и останавливается.

Для наглядности проиллюстрируем работу такой с помощью рис. 3.2 -3.7 .

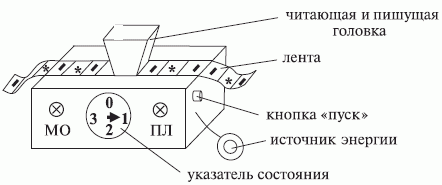
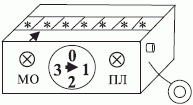
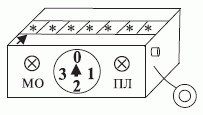
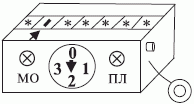
В исходном положении лента содержит только символы "пусто", го ловка размещается над ячейкой, помеченной стрелкой, а находится в состоянии , обнаруживает символ "пусто", сдвигается вправо на одну ячейку (см. рис. 3.3) и переходит в состояние 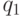(см. рис. 3.4). Затем заменяет символ "пусто" в текущей рабочей ячейке на символ 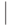(см. рис. 3.5) и переходит в состояние 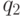(см. рис. 3.6). В этом положении согласно предписанию останавливается, о чем сигнализирует лампочка МО (см. рис. 3.7).

Рис. 3.2. Исходное положение

Рис. 3.3. Положение 1

Рис. 3.4. Положение 2

Рис. 3.5. Положение 3

Рис. 3.6. Положение 4

Рис. 3.7. Положение "останов"

В данном случае не требуется уточнять, что речь идет о вычислимых только по Тьюрингу функций, так как если функция вычислима по Тьюрингу, она вычислима и по Клини, и по Черчу, и по Маркову, и т. д.

Несмотря на кажущийся примитивизм выполняемых МТ "элементарных" действий, с их помощью можно представить алгоритм вычисления практически любой вычислимой функции. В частности, чтобы машина Тьюринга смогла реализовать приведенный ранее алгоритм,а суммирования достаточно, чтобы она имела три состояния: начальное , чтобы выполнить шаг 1, и два рабочих: 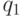если , и 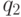, если