| Россия, Москва, МЭИ, 2006 |
Теория вычислений и машины Тьюринга
Алгоритмический подход исходит из необходимости оценки количества информации в индивидуальном объекте x относительно индивидуального объекта y [51]. В такой постановке можно дать только асимптотическую оценку количества информации, содержащейся в одной относительно большой последовательности символов относительно другой. В рамках такого подхода нет смысла говорить о количестве информации в последовательности 1010 относительно последовательности 0111. Но если взять конкретную таблицу случайных чисел достаточно большого объема и выписать для каждой ее цифры цифру, отвечающую количеству единиц в ее квадрате по правилу [51]:
то новая таблица случайных чисел будет содержать примерно 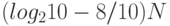 информации о первоначальной, где
информации о первоначальной, где  - число цифр в каждой таблице. Для алгоритмической меры информации
- число цифр в каждой таблице. Для алгоритмической меры информации 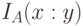 характерно, что равноценные варианты ее определения могут привести к значениям, отличающимся на константу
характерно, что равноценные варианты ее определения могут привести к значениям, отличающимся на константу 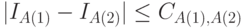 . Данная константа зависит от выбора универсального метода программирования, положенного в основу каждого из вариантов
(
. Данная константа зависит от выбора универсального метода программирования, положенного в основу каждого из вариантов
( 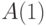 и
и 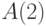 ) определения меры, то есть в рамках алгоритмического подхода максимум чего можно достичь:
) определения меры, то есть в рамках алгоритмического подхода максимум чего можно достичь: 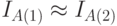
Следуя [51], будем рассматривать счетное множество "нумерованных объектов" 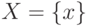 , каждому элементу которого поставлен в соответствие его номер
, каждому элементу которого поставлен в соответствие его номер 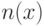 в виде конечной двоичной последовательности, начинающейся с единицы.
в виде конечной двоичной последовательности, начинающейся с единицы.
Считается:
- Соответствие между
 и множеством двоичных последовательностей
и множеством двоичных последовательностей 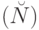 описанного вида взаимно однозначно.
описанного вида взаимно однозначно. -
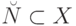 , функция
, функция 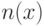 на
на 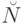 общерекурсивна, причем для
общерекурсивна, причем для 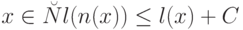 , где
, где 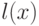 - длина двоичной последовательности
- длина двоичной последовательности 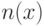 , а
, а 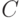 - некоторая константа.
- некоторая константа. - Вместе с
 и
и  в
в  входит упорядоченная пара
входит упорядоченная пара 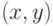 , номер этой пары есть общерекурсивная функция номеров
, номер этой пары есть общерекурсивная функция номеров  и
и  , а
, а 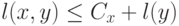 , где
, где 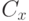 зависит только от
зависит только от  .
.
При таких условиях все результаты оценки "сложности" … и количества информации эквивалентны в смысле = при следующих преобразованиях:
- переход к новой нумерации
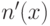 , которая обладает теми же свойствами, что и
, которая обладает теми же свойствами, что и 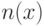 , и выражается общерекурсивно через
, и выражается общерекурсивно через 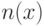 ;
; - включения системы
 в более обширную систему
в более обширную систему  и в предположении, что номера
и в предположении, что номера 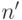 в расширенной системе для элементов первоначальной системы общерекурсивно выражаются через первоначальные номера
в расширенной системе для элементов первоначальной системы общерекурсивно выражаются через первоначальные номера 
Определение (А.Н. Колмогоров [51]): "относительной сложностью" объекта  при заданном
при заданном  будем считать минимальную длину
будем считать минимальную длину 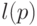 "программы"
"программы"  получения
получения  из
из  .
.
Длина 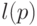 "программы"
"программы"  зависит от "метода программирования", что можно выразить функцией
зависит от "метода программирования", что можно выразить функцией 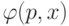 , которая ставит в соответствие программе
, которая ставит в соответствие программе  и объекту
и объекту  объект
объект  . Такая функция является частично рекурсивной и для нее:
. Такая функция является частично рекурсивной и для нее:
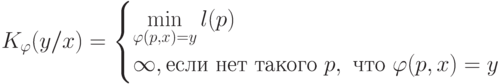 |
( 3.8) |
Функция 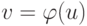 от
от 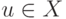 со значениями
со значениями 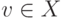 называется частично рекурсивной, если она порождается частично рекурсивной функцией преобразования номеров
называется частично рекурсивной, если она порождается частично рекурсивной функцией преобразования номеров ![n(v) = \Psi[n(u)]](/sites/default/files/tex_cache/ee956d9a87650a0d9789a3903c29394b.png) .
.
Частично рекурсивные функции, вообще говоря, не являются всюду определенными, и поэтому нет регулярного процесса для выяснения того, приведет ли программа 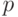 , примененная к объекту
, примененная к объекту  , вообще к какому-либо результату. По этой причине функция
, вообще к какому-либо результату. По этой причине функция 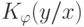 не обязана быть эффективно вычислимой (общерекурсивной) даже в случае, когда она заведомо конечна при любых
не обязана быть эффективно вычислимой (общерекурсивной) даже в случае, когда она заведомо конечна при любых  и
и  .
.
Теорема (А.Н. Колмогоров [51]): существует такая частично рекурсивная функция 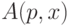 , что для любой другой частично рекурсивной функции
, что для любой другой частично рекурсивной функции 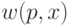 выполнено неравенство
выполнено неравенство 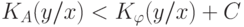 , где константа
, где константа 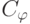 не зависит от
не зависит от  и
и  .
.
Доказательство этой теоремы опирается на существование универсальной частично рекурсивной функции 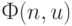 , которая обладает тем свойством, что, фиксируя надлежащим образом номер
, которая обладает тем свойством, что, фиксируя надлежащим образом номер  , можно получить любую другую частично рекурсивную функцию по формуле
, можно получить любую другую частично рекурсивную функцию по формуле 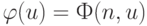 , где
, где 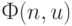 определена только в случае
определена только в случае 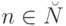 . Такая универсальная частично рекурсивная функция определяется соотношением:
. Такая универсальная частично рекурсивная функция определяется соотношением:
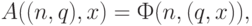
где 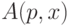 определена только в случае, когда
определена только в случае, когда  имеет вид
имеет вид 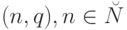 .
.
Функции 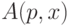 , удовлетворяющие теореме Колмогорова, а вместе с ней и определяемые ими методы программирования, принято называть асимптотически оптимальными, и для них "сложность"
, удовлетворяющие теореме Колмогорова, а вместе с ней и определяемые ими методы программирования, принято называть асимптотически оптимальными, и для них "сложность" 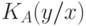 конечна при любых
конечна при любых  и
и  . Поэтому для двух таких функций
. Поэтому для двух таких функций  и
и 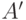 :
: 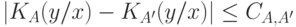 , где
, где 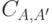 , не зависит от
, не зависит от  и
и  , то есть
, то есть  .
.
С учетом, что "сложность объекта  "
" 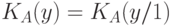 , "количество информации в
, "количество информации в  относительно
относительно  " определяется соотношением
" определяется соотношением ![I_{A} ( x : y) = [ K_{A}(y) - K_{A}(y/x)] \stackrel{\sim}{\succ} 0](/sites/default/files/tex_cache/9c872fe4ab9af0c3cadd4b24391f60da.png) , где символ
, где символ 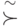 понимается в том смысле, что
понимается в том смысле, что 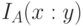 не меньше некоторой отрицательной константы
не меньше некоторой отрицательной константы 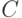 , зависящей только от условностей выбранного метода программирования. В результате в рамках алгоритмического подхода под "большим" понимается количество информации, для которого
, зависящей только от условностей выбранного метода программирования. В результате в рамках алгоритмического подхода под "большим" понимается количество информации, для которого 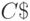 пренебрежимо мал, а
пренебрежимо мал, а 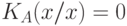 и
и 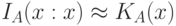 , как это имеет место в комбинаторном и вероятностном подходах.
, как это имеет место в комбинаторном и вероятностном подходах.
Из приведенных данных видно, что в рамках алгоритмического подхода избавиться от неопределенностей в оценке количества информации, связанных с константами 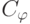 , можно только для определенных классов объектов
, можно только для определенных классов объектов  , фиксированных нумераций и фиксированных функций
, фиксированных нумераций и фиксированных функций  (методов программирования). Такие условия характерны для алгоритмически ориентированных вычислителей и "дочерних" нейро-ЭВМ, при выборе архитектуры которых имеет смысл дать ответ на вопрос о том, по какой схеме их строить: вычислительной или перечислительной.
(методов программирования). Такие условия характерны для алгоритмически ориентированных вычислителей и "дочерних" нейро-ЭВМ, при выборе архитектуры которых имеет смысл дать ответ на вопрос о том, по какой схеме их строить: вычислительной или перечислительной.
Все использованные А.Н. Колмогоровым частично рекурсивные функции вычислимы на машине Тьюринга, работающей с двузначным алфавитом и реализующей отображение [52] 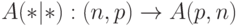 , где
, где 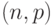 - введенная в МТ программа, порождающая 0-1-слова
- введенная в МТ программа, порождающая 0-1-слова 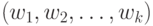 длины
длины  . Такой формализм позволяет решить центральную для теории вероятности проблему, связанную с определением "случайное событие". Традиционно с этим термином связывали бросание монеты в опыте Бернулли, что не корректно с точки зрения строгой математики, так как в этом случае к определению центрального понятия математической теории привлекается чисто физический процесс, с помощью которого невозможно определить никакое математическое свойство.
. Такой формализм позволяет решить центральную для теории вероятности проблему, связанную с определением "случайное событие". Традиционно с этим термином связывали бросание монеты в опыте Бернулли, что не корректно с точки зрения строгой математики, так как в этом случае к определению центрального понятия математической теории привлекается чисто физический процесс, с помощью которого невозможно определить никакое математическое свойство.
Отсюда и встает задача математического определения "случайной 0-1-последовательности", и сделать это надо так, чтобы основанная на этом определении математическая теория давала результаты, полностью согласованные с эмпирическими.
Первые попытки такой формализации "случайности" были предприняты фон Мизесом [53], который исходил из понятия "беспорядочной последовательности", считая, что "беспорядочность" является основным признаком "случайности". С этой целью он предложил называть бесконечную 0-1-последовательность случайной, если в ней относительная частота появления "единиц" стремится к 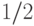 и это свойство сохраняется при переходе к произвольной подпоследовательности с использованием любого правила выбора. При таком подходе главная трудность состояла в строгом определении термина "правило выбора". Такое уточнение было получено А. Вальдом, но вскоре вся программа фон Мизеса было опровергнута Д. Виллем [52], который построил 0-1-последовательность, удовлетворяющую требованиям фон Мизеса с частотой "единиц" не менее
и это свойство сохраняется при переходе к произвольной подпоследовательности с использованием любого правила выбора. При таком подходе главная трудность состояла в строгом определении термина "правило выбора". Такое уточнение было получено А. Вальдом, но вскоре вся программа фон Мизеса было опровергнута Д. Виллем [52], который построил 0-1-последовательность, удовлетворяющую требованиям фон Мизеса с частотой "единиц" не менее 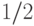 .
.
Затем в теории вероятности наступил "колмогоровский" период, когда ее стали рассматривать как прикладную теорию меры. В этом случае речь может идти только о множествах последовательностей, а не об индивидуальных последовательностях. Несмотря на успехи своей теории, А.Н. Колмогоров все же вернулся к логическим основам теории вероятности [54] и предложил использовать (3.8) для оценки энтропии:
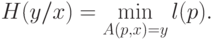
Отсюда, существуют 0-1-последовательности, для которых энтропия не меньше их длины 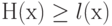 . По здравому смыслу такие последовательности и следует относить к "случайным", так как в них отсутствуют закономерности, сокращающие длину программы для машин Тьюринга.
. По здравому смыслу такие последовательности и следует относить к "случайным", так как в них отсутствуют закономерности, сокращающие длину программы для машин Тьюринга.
Таким образом, если программа  "сложнее", чем порождаемая ею последовательность
"сложнее", чем порождаемая ею последовательность  , то, по Колмогорову, такую последовательность следует считать "случайной".
, то, по Колмогорову, такую последовательность следует считать "случайной".
Системотехнические выводы по лекции 3
- Традиционно считается, что нейрокомпьютерные технологии вторичны по отношению к классическим фон-неймановским технологиям, так как в формальных нейронах логические преобразования реализуются через арифметические. В реальности для работы любого вычислителя достаточно двух традиционных для нейрокомпьютерной техники "элементарных" операций: "ассоциативная выборка" и "подстановка" (замещение) символов. Этот вывод парадоксален только на первый взгляд, так как реальные нейроны появились задолго до того, как человек стал использовать понятие "число". Поэтому для обеспечения жизнедеятельности реальных нейронов можно было привлечь только "нечисленные" методы и средства "ассоциативной выборки" и "подстановки" (замещения) символов.
Отсюда, имеются достаточные основания считать первичными нейрокомпьютерные технологии, а вторичными - традиционные вычислительные технологии, на схемотехническом уровне которых в неявном виде для каждой арифметико-логической операции используется "схемотехнически сжатые" таблицы ассоциативной выборки и подстановки символов
 .
. - Первичность нейрокомпьютерных технологий по отношению к компьютерным предопределяет сама логика формализации: от эмпирической таблицы к аналитическому или алгоритмическому представлению. Поэтому разница между компьютерными и нейрокомпьютер-ными технологиями в конечном счете состоит в уровне доступности пользователя к операционному базису. В нейрокомпьютерных технологиях пользователю доступен сетевой уровень управления и "элементарные операции", реализуемые отдельными элементами сети. В традиционных вычислительных технологиях с помощью "элементарных операций" (микрокоманд) производитель процессора формирует ассемблерные команды, которые для пользователя уже являются "неделимой единицей проекта". В итоге задание пользователя в нейрокомпьютерных технологиях можно представить тривиальной таблицей соответствия между входными воздействиями и требуемыми реакциями. В традиционных вычислительных технологиях требуется не только формализованное представление задания, но и алгори тм, регламентирующий в конечном счете последовательность выполнения ассемблерных команд.
- Само понятие "алгоритм" уже предполагает некоторую последовательность информационно связанных преобразований конструктивных объектов. Это ограничивает реально реализуемые схемы распараллеливания вычислений векторизацией и конвейеризацией соответственно информационно независимых и информационно зависимых подпоследовательностей преобразований, а также их комбинациями типа векторно-конвейерная или конвейерно-векторная.
- Контекстным системотехническим обоснованием экстенсиональной эквивалентности традиционных и нейроподобных ЭВМ служит сводимость вычислительных по Тьюрингу процедур к перечислимым по Тьюрингу процедурам, первые из которых составляют операционный базис ЭВМ одной из традиционных архитектур, а вторые - одной из ней-рокомпьютерных архитектур. Поэтому имеются достаточные основания утверждать, что любой нейро-ЭВМ можно поставить в соответствие классическую ЭВМ, эквивалентную по вычисляемой функции, и наоборот.
- Оценку алгоритмической сложности реальных (нейро)компьютерных реализаций можно провести только с определенной погрешностью и при достаточно жестких ограничениях на используемые вычислительные и/или перечислительные алгоритмы, что характерно для алгоритмически ориентированных областей применения традиционных вычислителей и "дочерних" нейро-ЭВМ, а не для машин общего назначения.

