Числовые характеристики распределений
Другие числовые характеристики распределений
Распределения можно характеризовать и многими другими показателями, большинство из которых находит основное применение в статистике. Здесь мы только кратко познакомимся с их определениями.
Медианой
распределения случайной величины  называется любое из чисел
называется любое из чисел 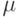 таких, что
таких, что
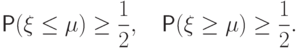
Медиана распределения всегда существует, но может быть не единственна. Так,
у биномиального
распределения с параметрами 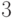 и
и  медианой
будет
любое число из отрезка
медианой
будет
любое число из отрезка ![[1,\,2]](/sites/default/files/tex_cache/208d1553b52fe522bc5713f62182b18c.png) . Действительно,
. Действительно,  принимает значения
принимает значения  ,
,  ,
, 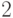 и
и 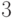 с
вероятностями соответственно
с
вероятностями соответственно  ,
,  ,
,  и
и  .
Поэтому для всех
.
Поэтому для всех ![\mu\in[1,\,2]](/sites/default/files/tex_cache/5799f31cfaa0de2d927ae37daf716054.png)
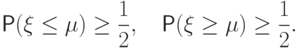
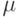 берут середину
"отрезка медиан".
берут середину
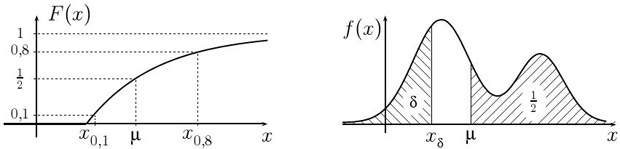
"отрезка медиан".Для распределений с непрерывной и строго монотонной функцией распределения  медиана является единственным решением уравнения
медиана является единственным решением уравнения 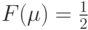 .
Это точка, левее и правее которой на числовой прямой сосредоточено
ровно по половине всей вероятностной "массы" (
рис.
10.1). Если
распределение
имеет плотность
.
Это точка, левее и правее которой на числовой прямой сосредоточено
ровно по половине всей вероятностной "массы" (
рис.
10.1). Если
распределение
имеет плотность  , то площади каждой из областей
под графиком плотности слева и справа от точки
, то площади каждой из областей
под графиком плотности слева и справа от точки 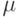 одинаковы.
одинаковы.
Медиана является одной из квантилей
распределения. Пусть для простоты функция распределения  непрерывна и строго монотонна. Тогда квантилью уровня
непрерывна и строго монотонна. Тогда квантилью уровня 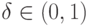 называется решение уравнения
называется решение уравнения 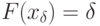 .
.
Квантиль 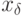 уровня
уровня  отрезает от
области под графиком плотности
область с площадью
отрезает от
области под графиком плотности
область с площадью  слева от себя, и с площадью
слева от себя, и с площадью 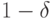 - справа.
Медиана является квантилью уровня
- справа.
Медиана является квантилью уровня 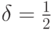 .
.
Квантили уровней, кратных 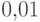 , в прикладной статистике
называют процентилями,
квантили уровней, кратных
, в прикладной статистике
называют процентилями,
квантили уровней, кратных  , - децилями,
уровней, кратных
, - децилями,
уровней, кратных  , - квартилями.
, - квартилями.
Модой абсолютно непрерывного распределения
называют любую
точку локального максимума плотности распределения. Для дискретных
распределений модой считают любое значение 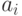 , вероятность
которого
больше, чем вероятности соседних значений (соседнего, если таковое одно).
, вероятность
которого
больше, чем вероятности соседних значений (соседнего, если таковое одно).
Для нормального распределения 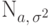 медиана, математическое ожидание и мода равны
медиана, математическое ожидание и мода равны  .
Распределение, обладающее единственной модой, называют
унимодальным.
Идеальным примером унимодального распределения является нормальное
распределение.
Плотность произвольного унимодального распределения может быть как
более плоской (равномерное распределение), так и более
"островершинной"
(показательное распределение) по сравнению с плотностью нормального
распределения,
может быть симметричной либо наклоненной в одну сторону. Для описания таких
свойств плотности используют коэффициент
эксцесса и
коэффициент асимметрии.
.
Распределение, обладающее единственной модой, называют
унимодальным.
Идеальным примером унимодального распределения является нормальное
распределение.
Плотность произвольного унимодального распределения может быть как
более плоской (равномерное распределение), так и более
"островершинной"
(показательное распределение) по сравнению с плотностью нормального
распределения,
может быть симметричной либо наклоненной в одну сторону. Для описания таких
свойств плотности используют коэффициент
эксцесса и
коэффициент асимметрии.
Коэффициентом асимметрии распределения с конечным третьим моментом называется число

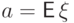 ,
,  .
.Для симметричных распределений коэффициент асимметрии равен нулю.
Если 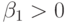 , то график плотности распределения имеет более
крутой наклон
слева и более пологий - справа; при
, то график плотности распределения имеет более
крутой наклон
слева и более пологий - справа; при  -
наоборот.
-
наоборот.
Коэффициентом эксцесса распределения с конечным четвертым моментом называется число

Для всех нормальных распределений коэффициент эксцесса равен нулю.
Действительно, для  величина
величина 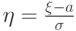 имеет
стандартное нормальное
распределение. Четвертый момент этого распределения равен трем:
имеет
стандартное нормальное
распределение. Четвертый момент этого распределения равен трем: 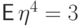 ( вычислить аналогично второму моменту в примере 60 ).
Поэтому
( вычислить аналогично второму моменту в примере 60 ).
Поэтому 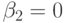 .
.
При 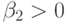 плотность распределения имеет более острую
вершину, чем у нормального
распределения, при
плотность распределения имеет более острую
вершину, чем у нормального
распределения, при 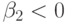 , наоборот, более плоскую.
, наоборот, более плоскую.