Числовые характеристики распределений
Дисперсия и моменты старших порядков
Определение 37.
Пусть 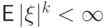 . Число
. Число  называется моментом порядка
называется моментом порядка 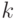 или
или 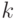 -м моментом
случайной величины
-м моментом
случайной величины  ,
число
,
число 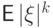 называется абсолютным
называется абсолютным 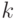 -м
моментом,
-м
моментом, 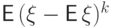 называется центральным
называется центральным 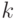 -м моментом,
и
-м моментом,
и 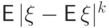 -
абсолютным центральным
-
абсолютным центральным 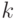 -м моментом} случайной величины
-м моментом} случайной величины  .
Число
.
Число 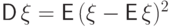 (центральный момент второго порядка) называется
дисперсией
случайной величины
(центральный момент второго порядка) называется
дисперсией
случайной величины  .
.
Пример 52.
Пусть, скажем, случайная величина  принимает значение
принимает значение  с вероятностью
с вероятностью  и значение
и значение  с вероятностью
с вероятностью  . Посмотрим, как моменты
разных
порядков реагируют на большие, но маловероятные значения
случайной величины:
. Посмотрим, как моменты
разных
порядков реагируют на большие, но маловероятные значения
случайной величины:
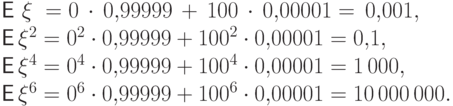
Пример 53.
Дисперсия 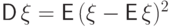 есть
"среднее значение квадрата отклонения случайной величины
есть
"среднее значение квадрата отклонения случайной величины  от своего
среднего". Посмотрим, за что эта величина отвечает.
от своего
среднего". Посмотрим, за что эта величина отвечает.
Пусть случайная величина  принимает значения
принимает значения  с равными вероятностями, а случайная величина
с равными вероятностями, а случайная величина  -
значения
-
значения  с равными вероятностями.
Тогда
с равными вероятностями.
Тогда 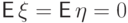 , поэтому
, поэтому 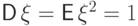 ,
,  .
Говорят, что дисперсия характеризует степень разброса
значений случайной величины вокруг ее математического ожидания.
.
Говорят, что дисперсия характеризует степень разброса
значений случайной величины вокруг ее математического ожидания.
Определение 38.
Число  называют
среднеквадратическим отклонением случайной величины
называют
среднеквадратическим отклонением случайной величины  .
.
Чтобы прояснить связь моментов разных порядков, докажем несколько неравенств. Во-первых, получим очевидное утверждение, обеспечивающее существование моментов меньших порядков, если существуют моменты более высокого порядка.
Теорема 31.
Если существует момент порядка 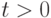 случайной величины
случайной величины  , то
существуют и ее моменты порядка
, то
существуют и ее моменты порядка  при
при 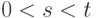 .
.
Доказательство. Для любого числа 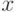 верно неравенство
верно неравенство
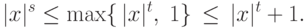
 при
при 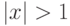 , и
, и 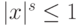 при
при  .
.Из этого неравенства следует, что 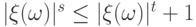 для всех
для всех 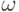 . Но следствие 11 позволяет
из неравенства для случайных величин получить такое же
неравенство для их математических ожиданий:
. Но следствие 11 позволяет
из неравенства для случайных величин получить такое же
неравенство для их математических ожиданий:
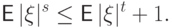
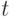 существует, т.е.
существует, т.е. 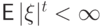 . Поэтому и
. Поэтому и 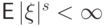 .
.Докажем еще одно чрезвычайно полезное неравенство.
Теорема 32 (неравенство Йенсена).
Пусть вещественнозначная функция 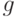 "выпукла вниз",
т.е. ее надграфик есть выпуклое множество. Тогда для
любой случайной величины
"выпукла вниз",
т.е. ее надграфик есть выпуклое множество. Тогда для
любой случайной величины  с конечным первым моментом верно
неравенство:
с конечным первым моментом верно
неравенство: 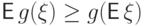 .
Для вогнутых функций знак неравенства
меняется на противоположный.
.
Для вогнутых функций знак неравенства
меняется на противоположный.
Доказательство. Нам понадобится следующее свойство.
Лемма 6.
Пусть функция 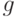 выпукла. Тогда для всякого
выпукла. Тогда для всякого  найдется число
найдется число 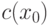 такое, что при всех
такое, что при всех 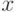
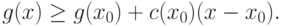
Это свойство очевидно и означает, что график выпуклой функции лежит полностью выше любой из касательных к этому графику.
Возьмем в условиях леммы 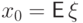 ,
,  .
Тогда
.
Тогда
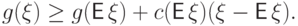
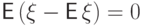 , и неравенство
между математическими ожиданиями сохраняется по следствию 11,
то
, и неравенство
между математическими ожиданиями сохраняется по следствию 11,
то 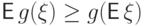 .
.Следующее неравенство связывает моменты разных порядков.
Следствие 13.
Если 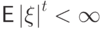 , то для любого
, то для любого 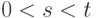
![\sqrt[\mbox{\small $s$ }]{{\mathsf E\,}{|\xi|}^s} \le
\sqrt[\mbox{\small $t$ }]{{\mathsf E\,}{|\xi|}^t}](/sites/default/files/tex_cache/957bedd7a78784e259ce70a317aa89f1.png)
Доказательство.
Поскольку 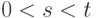 , то
, то  - выпуклая
функция.
По неравенству Йенсена для
- выпуклая
функция.
По неравенству Йенсена для  ,
,
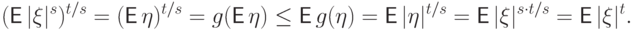
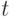 .
.Из неравенства Йенсена вытекают, например, неравенства:
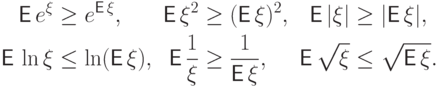
 .
.
