Многомерные распределения
Совместное распределение
Пусть случайные величины 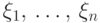 заданы на одном
вероятностном пространстве
заданы на одном
вероятностном пространстве  .
.

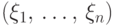 или
функцией совместного распределения случайных величин
или
функцией совместного распределения случайных величин 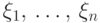 .
.Перечислим свойства функции совместного распределения.
Для простоты обозначений ограничимся
вектором  из двух величин.
из двух величин.
(F0) Для любых 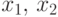 верно неравенство:
верно неравенство:  .
.
(F1)  не убывает по каждой
координате
вектора
не убывает по каждой
координате
вектора  .
.
(F2) Для любого 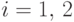 существует
существует 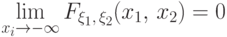 .
Существует двойной предел
.
Существует двойной предел  .
.
(F3) Функция  по каждой
координате
вектора
по каждой
координате
вектора  непрерывна слева.
непрерывна слева.
(F4) Чтобы по функции совместного распределения восстановить функции
распределения  и
и  в отдельности, следует
устремить мешающую
переменную к
в отдельности, следует
устремить мешающую
переменную к  :
:
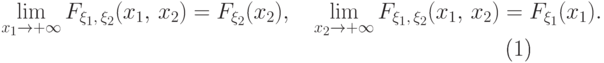 |
( 14) |
Доказательство всех этих свойств совершенно аналогично одномерному случаю.
Но теперь свойств (F0)-(F3) не хватает для описания
класса функций совместного распределения. Иначе говоря,
выполнение этих свойств для некоторой функции 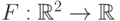 не гарантирует, что эта функция является функцией распределения
некоторого случайного вектора.
не гарантирует, что эта функция является функцией распределения
некоторого случайного вектора.
Упражнение. Доказать, что функция

 хотя бы потому, что, найдись такой вектор, найдется и прямоугольник
хотя бы потому, что, найдись такой вектор, найдется и прямоугольник  , "вероятность" попасть в
который
(вычисленная с помощью этой якобы "функции распределения")
отрицательна:
, "вероятность" попасть в
который
(вычисленная с помощью этой якобы "функции распределения")
отрицательна:  .
.Легко убедиться, что
вероятность вектору  попасть
в прямоугольник
попасть
в прямоугольник  по функции
распределения этого вектора вычисляется так:
по функции
распределения этого вектора вычисляется так:  .
.
Дополнительно к свойствам (F0)-(F3) от функции  требуют
неотрицательности этого выражения
(при любых
требуют
неотрицательности этого выражения
(при любых 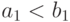 ,
,  ).
).
Типы многомерных распределений
Ограничимся рассмотрением двух типичных случаев: когда
совместное
распределение координат случайного вектора  либо дискретно, либо абсолютно непрерывно. Заметим, что сингулярные совместные
распределения тоже не являются редкостью, в отличие от одномерного случая:
стоит бросить точку наудачу на отрезок на плоскости, и мы получим
сингулярное совместное распределение ( доказать ).
либо дискретно, либо абсолютно непрерывно. Заметим, что сингулярные совместные
распределения тоже не являются редкостью, в отличие от одномерного случая:
стоит бросить точку наудачу на отрезок на плоскости, и мы получим
сингулярное совместное распределение ( доказать ).
Определение 29.
Случайные величины  ,
,  имеют
дискретное совместное распределение,
если существует конечный или счетный
набор пар чисел
имеют
дискретное совместное распределение,
если существует конечный или счетный
набор пар чисел 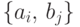 такой, что
такой, что

 -й строки и
-й строки и 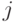 -го столбца которой стоит
вероятность
-го столбца которой стоит
вероятность  , называют
таблицей совместного распределения случайных величин
, называют
таблицей совместного распределения случайных величин  и
и  .
.Таблицы распределения каждой из случайных величин  ,
,  в отдельности (таблицы частных,
или маргинальных распределений)
восстанавливаются по таблице совместного
распределения с помощью формул
в отдельности (таблицы частных,
или маргинальных распределений)
восстанавливаются по таблице совместного
распределения с помощью формул

 ,
, 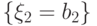 ,
,  есть полная группа событий,
и поэтому событие
есть полная группа событий,
и поэтому событие 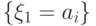 раскладывается в объединение
попарно несовместных
событий:
раскладывается в объединение
попарно несовместных
событий: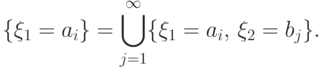
Определение 30.
Случайные величины  ,
,  имеют абсолютно непрерывное совместное распределение,
если существует неотрицательная функция
имеют абсолютно непрерывное совместное распределение,
если существует неотрицательная функция 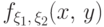 такая, что для любого множества
такая, что для любого множества 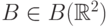 имеет место
равенство
имеет место
равенство
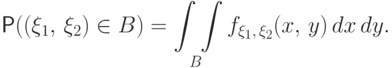
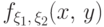 существует, она
называется
плотностью совместного распределения случайных
величин
существует, она
называется
плотностью совместного распределения случайных
величин  .
.Достаточно, если двойной интеграл по множеству  читатель
будет понимать
как объем области под графиком функции
читатель
будет понимать
как объем области под графиком функции 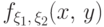 над множеством
над множеством  в плоскости переменных
в плоскости переменных  ,
как показано на
рис.
8.1.
,
как показано на
рис.
8.1.
Плотность совместного распределения обладает такими же свойствами, как и плотность распределения одной случайной величины:
(f1) неотрицательность: 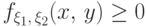 для любых
для любых 
(f2) нормированность:

Справедливо и обратное: любая функция, обладающая этими свойствами, является плотностью некоторого совместного распределения. Доказательство этого факта ничем не отличается от одномерного случая.
Если случайные величины  ,
,  имеют абсолютно непрерывное совместное распределение,
то для любых
имеют абсолютно непрерывное совместное распределение,
то для любых 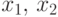 имеет место равенство
имеет место равенство

Если совместное распределение абсолютно непрерывно, то
по функции совместного распределения его плотность находится как
смешанная частная производная:  для почти всех
для почти всех  .
.
Из существования плотностей  и
и  не
следует абсолютная непрерывность
совместного распределения этих случайных величин. Например, вектор
не
следует абсолютная непрерывность
совместного распределения этих случайных величин. Например, вектор  принимает значения только на диагонали в
принимает значения только на диагонали в  и уже поэтому не
имеет плотности
распределения (его распределение сингулярно).
Обратное же свойство, как показывает следующая теорема, всегда верно: если
совместное распределение абсолютно непрерывно,
то и частные распределения тоже таковы.
и уже поэтому не
имеет плотности
распределения (его распределение сингулярно).
Обратное же свойство, как показывает следующая теорема, всегда верно: если
совместное распределение абсолютно непрерывно,
то и частные распределения тоже таковы.
Теорема 24.
Если случайные величины  и
и  имеют
абсолютно непрерывное
совместное распределение с плотностью
имеют
абсолютно непрерывное
совместное распределение с плотностью  ,
то
,
то  и
и  в отдельности также имеют абсолютно
непрерывное распределение с плотностями:
в отдельности также имеют абсолютно
непрерывное распределение с плотностями:

Для  плотности случайных величин
плотности случайных величин 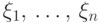 по
плотности их совместного распределения
по
плотности их совместного распределения 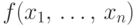 находятся интегрированием функции
находятся интегрированием функции  по всем "лишним"
координатам.
по всем "лишним"
координатам.
Доказательство. Например, в силу равенств (14),