|
поддерживаю выше заданые вопросы
|
Умножение разреженных матриц
Параллельный вариант метода прогонки
Рассмотрим теперь схему распараллеливания метода прогонки при использовании p потоков. Пусть нужно решить трехдиагональную систему линейных уравнений
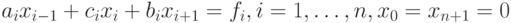 |
( 7.29) |
с использованием p параллельных потоков.
Применим блочный подход к разделению данных: пусть каждый поток обрабатывает 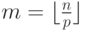 строк матрицы A, т.е. k-й поток обрабатывает строки с номерами
строк матрицы A, т.е. k-й поток обрабатывает строки с номерами 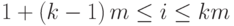 . Для простоты изложения мы предполагаем, что число уравнений в системе кратно числу потоков, в общем случае изменится только число уравнений в последнем потоке. Ниже представлено разделение данных для трех потоков в случае системы из 12 уравнений.
. Для простоты изложения мы предполагаем, что число уравнений в системе кратно числу потоков, в общем случае изменится только число уравнений в последнем потоке. Ниже представлено разделение данных для трех потоков в случае системы из 12 уравнений.
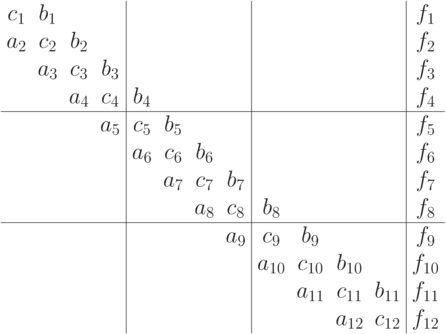
В пределах полосы матрицы, обрабатываемой k-м потоком, можно организовать исключение поддиагональных элементов матрицы (прямой ход метода). Для этого осуществляется вычитание строки i, умноженной на константу 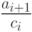 , из строки i+1 с тем, чтобы результирующий коэффициент при неизвестной xi в (i+1)-й строке оказался нулевым.
, из строки i+1 с тем, чтобы результирующий коэффициент при неизвестной xi в (i+1)-й строке оказался нулевым.
Если исключение первым потоком поддиагональных переменных не добавит в матрицу новых коэффициентов, то исключение поддиагональных элементов в остальных потоках приведет к возникновению столбца отличных от нуля коэффициентов: во всех блоках (кроме первого) число ненулевых элементов в строке не изменится, но изменится структура уравнений.
Модификации также подвергнутся элементы вектора правой части. Матрица (7.30) иллюстрирует данный процесс, чертой сверху отмечены элементы, которые будут модифицированы.
 |
( 7.30) |
Затем выполняется обратный ход алгоритма – каждый поток исключает наддиагональные элементы, начиная с последнего.

После выполнения обратного хода матрица стала блочной. Исключим из нее внутренние строки каждой полосы, в результате получим систему уравнений относительно части исходный неизвестных, частный вид которой представлен ниже.
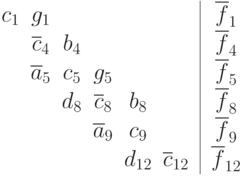
Данная система будет содержать 2p уравнений, и будет трехдиагональной. Ее можно решить последовательным методом прогонки. После того, как эта система будет решена, станут известны значения неизвестных на границах полос разделения данных. Далее можно за один проход найти значения внутренних переменных.
Рассмотренный способ распараллеливания уже дает хорошие результаты, но можно использовать лучшую стратегию исключения неизвестных. Прямой ход нового алгоритма будет таким же, а во время обратного хода каждый поток исключает наддиагональные элементы, начиная со своего предпоследнего, и заканчивая последним для предыдущего потока. Матрица (7.31) иллюстрирует данный процесс.
 |
( 7.31) |
Изменение порядка исключения переменных в обратном ходе алгоритма приводит к тому, что можно сформировать вспомогательную задачу меньшего размера. Исключим из матрицы все строки каждой полосы, кроме последней, в результате получим систему уравнения относительно части исходный неизвестных, частный вид которой представлен ниже.
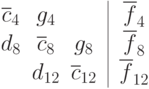
Даная система будет содержать всего p уравнений, и также будет трехдиагональной. Ее можно решить последовательным методом прогонки (так как для систем с общей памятью число потоков p будет не слишком велико, применять для решения вспомогательной системы даже параллельный метод встречной прогонки нецелесообразно). После того, как эта система будет решена, станут известны значения неизвестных на нижних границах полос разделения данных. Далее можно за один проход найти значения внутренних переменных в каждом потоке.
Оценим трудоемкость рассмотренного параллельного варианта метода прогонки. В соответствии с введенными ранее обозначениями n есть порядок решаемой системы линейных уравнений, а p, 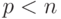 , обозначает число потоков. Тем самым, матрица коэффициентов А имеет размер
, обозначает число потоков. Тем самым, матрица коэффициентов А имеет размер  и, соответственно,
и, соответственно, 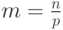 есть размер полосы матрицы А на каждом процессоре.
есть размер полосы матрицы А на каждом процессоре.
При выполнении прямого хода алгоритма на каждой итерации каждый процессор должен осуществить исключение в пределах своей полосы поддиагональных элементов (что требует 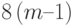 операций) и наддиагональных элементов (что требует 7m операций).
операций) и наддиагональных элементов (что требует 7m операций).
Затем следует произвести сборку вспомогательной трехдиагональной системы уравнений в одном потоке, и осуществить ее решение методом прогонки. В соответствии с оценкой (7.26) затраты на выполнение этого чисто последовательного этапа составят порядка 10p операций.
На следующем этапе алгоритма каждый процессор выполняет обратный ход алгоритма, который потребует 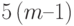 операций. Таким образом, общую трудоемкость параллельного метода прогонки можно оценить как
операций. Таким образом, общую трудоемкость параллельного метода прогонки можно оценить как
 |
( 7.32) |
Как результат выполненного анализа, показатели ускорения и эффективности параллельного варианта метода прогонки могут быть определены при помощи соотношений следующего вида:
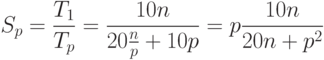 |
( 7.33) |
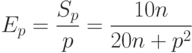
Из приведенных соотношений видно, что в случае решения системы уравнений с большим числом неизвестных, при котором  , показатели ускорения и эффективности будут определяться как
, показатели ускорения и эффективности будут определяться как
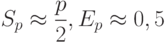 |
( 7.34) |
Результаты вычислительных экспериментов
Вычислительные эксперименты для оценки эффективности параллельного варианта метода прогонки для решения трехдиагональных систем линейных уравнений проводились на аппаратуре, технические характеристики которой указаны во введении. Также следует отметить, что для простоты написания параллельных программ нами рассматривались задачи размера, кратного 8, чтобы размер блоков был одинаков для всех потоков. С целью формирования матрицы с диагональным преобладанием элементы на побочных диагоналях матрицы генерировались в диапазоне от 0 до 100, а элемент на главной диагонали был равен удвоенной сумме элементов в строке.
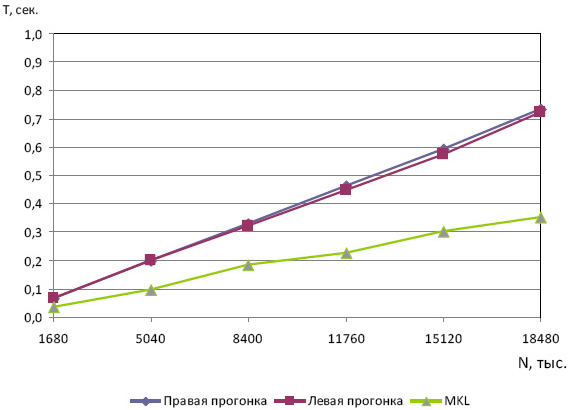
Сначала приведем результаты сравнения реализованной нами правой и левой прогонки со специальной функцией библиотеки Intel MKL, решающей трехдиагональные системы с диагональным преобладанием. Результаты, отражающие зависимость времени решения задачи T от ее размера N, приведены на рис. 7.9.
Результаты экспериментов демонстрируют двукратное отставание от библиотеки Intel MKL по времени, что является неплохим показателем.
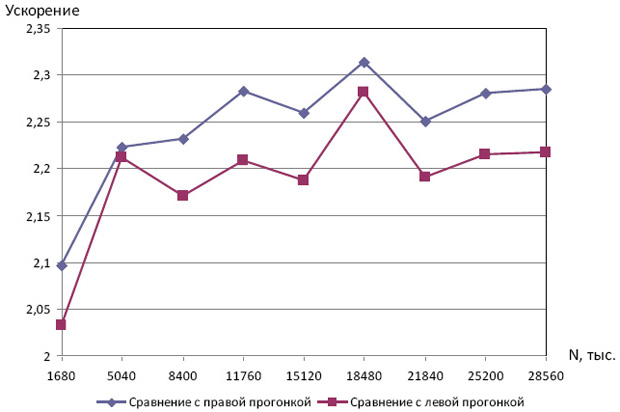
Далее рассмотрим эффект, который дает использование встречной прогонки в двух потоках: проведем сравнение параллельной встречной прогонки с правой и левой прогонками. Результаты, отражающие зависимость ускорения по отношению к правой и левой прогонкам от размера задачи N приведены на рис. 7.10.
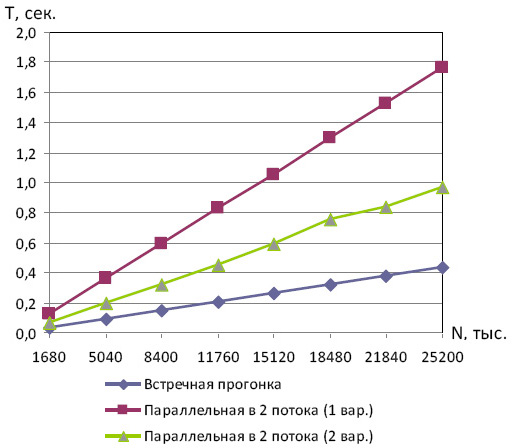
Перед тем, как переходить к экспериментам с большим числом потоков, выясним, какой из алгоритмов является наиболее быстрым в двухпоточной программе. Для сравнения будем использовать метод встречной прогонки, и два способа распараллеливания, описанных в п. 7.3.2.
Как и следовало ожидать, наиболее быстродействующим оказался метод встречной прогонки. Однако встречную прогонку можно использовать только в двух потоках, для распараллеливания на большее число потоков нужно использовать вторую модификацию алгоритма, описанную в п. 7.3.2, которая обладает большей трудоемкостью, но и большей масштабируемостью. Ниже приведены результаты вычислительных экспериментов, полученные при использовании данной модификации параллельного метода прогонки.
| n, тыс. | 1 поток | Параллельный алгоритм | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 потока | 4 потока | 6 потоков | 8 потоков | ||||||
| T | S | T | S | T | S | T | S | ||
| 1680 | 0,06 | 0,07 | 0,94 | 0,03 | 2,03 | 0,03 | 2,10 | 0,03 | 2,03 |
| 5040 | 0,20 | 0,20 | 1,00 | 0,11 | 1,83 | 0,09 | 2,29 | 0,09 | 2,14 |
| 8400 | 0,32 | 0,32 | 0,99 | 0,17 | 1,85 | 0,15 | 2,18 | 0,14 | 2,26 |
| 11760 | 0,45 | 0,45 | 0,98 | 0,23 | 1,91 | 0,20 | 2,25 | 0,20 | 2,20 |
| 15120 | 0,57 | 0,59 | 0,97 | 0,31 | 1,84 | 0,26 | 2,18 | 0,27 | 2,16 |
| 18480 | 0,72 | 0,76 | 0,95 | 0,41 | 1,78 | 0,32 | 2,25 | 0,31 | 2,31 |
| 21840 | 0,83 | 0,84 | 0,99 | 0,45 | 1,84 | 0,38 | 2,20 | 0,37 | 2,22 |
| 25200 | 0,96 | 0,97 | 0,99 | 0,53 | 1,80 | 0,43 | 2,25 | 0,44 | 2,19 |
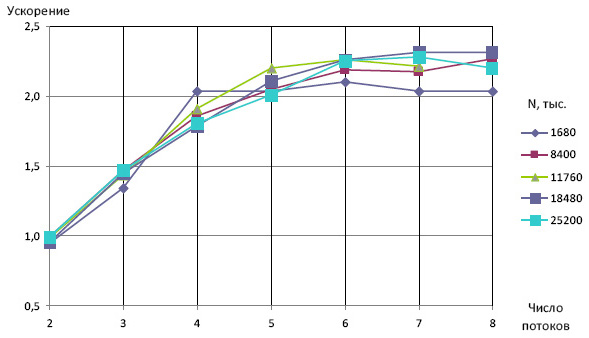
На рис. 7.12 приведен график зависимости ускорения от числа потоков при использовании модификации алгоритма из п. 1.2.2. Видно, что при p<6 ускорение в целом соответствует оценке (7.34), полученной с помощью подсчета числа операций, необходимых для работы метода.
Вернемся опять к рассмотрению системы линейных уравнений
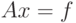
с трехдиагональной матрицей A, удовлетворяющей условию строгого диагонального преобладания. В п. 7.3 мы уже познакомились с методом прогонки для решения подобных систем. Анализ формул метода прогонки показывает, что в некоторых случаях метод может давать большую погрешность. Потенциальным источником погрешности являются формулы для вычисления "прогоночных" коэффициентов, которые содержат операцию деления на разность близких по значению величин.
Метод редукции, который будет рассмотрен ниже, свободен от этого недостатка и, кроме того, при реализации на современных вычислительных системах он показывает большую эффективность по сравнению с методом прогонки. Основное ограничение метода редукции состоит в том, что он применим лишь для матриц размера, равного степени двойки, в отличие от метода прогонки, применимого для матриц любого размера.
Следует отметить, что существует обобщение метода редукции на случай блочных трехдиагональных матриц (см. [4]). В этом случае число блоков должно быть равно степени двойки, а основная идея метода остается неизменной (лишь операция деления заменяется на операцию умножения на обратную матрицу, что подразумевает хорошую обратимость блоков матрицы A).
Последовательный алгоритм
Для удобства последующих обозначений запишем систему в виде
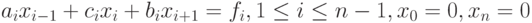 |
( 7.35) |
Идея метода редукции состоит в последовательном исключении из системы (7.35) неизвестных сначала с нечетными номерами, затем с номерами, кратными 2 (но не кратными 4), и т.д., (прямой ход) и восстановлении значений нечетных переменных на основании известных значений переменных с четными номерами (обратный ход).
Выпишем три идущие подряд уравнения системы (7.35) с номерами i-1, i, i+1, где i – четное число

Умножая первое из указанных уравнений на коэффициент  , последнее – на коэффициент
, последнее – на коэффициент 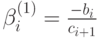 и складывая полученные уравнения со вторым, получим
и складывая полученные уравнения со вторым, получим
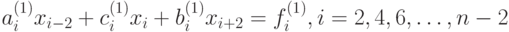 |
( 7.36) |
где
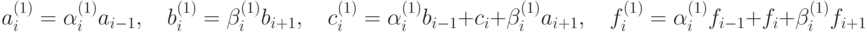
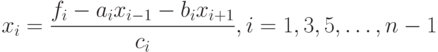
Очевидно, что систему (7.36) можно решить, используя описанный процесс рекурсивно (так как число переменных в ней будет 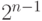 ).
).
Таким образом, на втором шаге алгоритма из системы будут (7.36) исключены переменные с номерами, кратными 2, но не кратными 4. В результате l-го шага процесса исключения получим систему
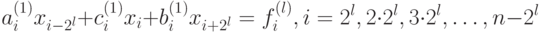 |
( 7.37) |
где
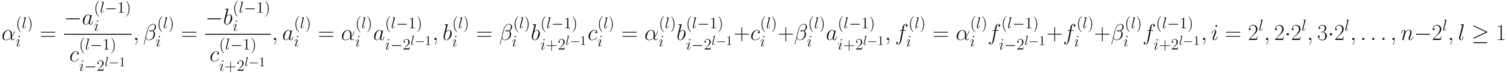 |
( 7.38) |
Здесь использованы обозначения 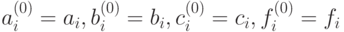
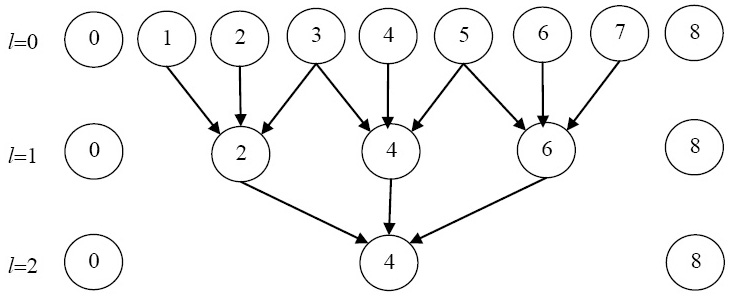
Графическая иллюстрация схемы исключения переменных для случая n=8 приведена на рис. 7.13. При l=0 система уравнений совпадает с исходной и содержит все неизвестные. На рис. 7.13 номера неизвестных переменных, входящих в систему, отмечены в кружочках. На первом этапе (l=1) происходит исключение неизвестных с нечетными номерами, в результате чего получаем систему, содержащую только четные переменные. Стрелки указывают, какие переменные участвовали в исключении. На последнем этапе (l=2) остается только одно уравнение, связывающее 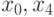 и
и 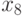 .
.
В общем случае процесс исключения закончится на  -м шаге,
-м шаге,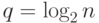 , когда система (7.37) будет состоять из одного уравнения относительно переменной
, когда система (7.37) будет состоять из одного уравнения относительно переменной 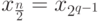 . Из этого уравнения, учитывая
. Из этого уравнения, учитывая 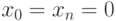 , найдем
, найдем
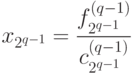
Остальные переменные определяются по формулам
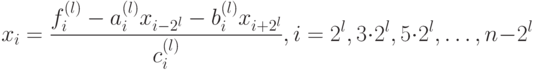 |
( 7.39) |
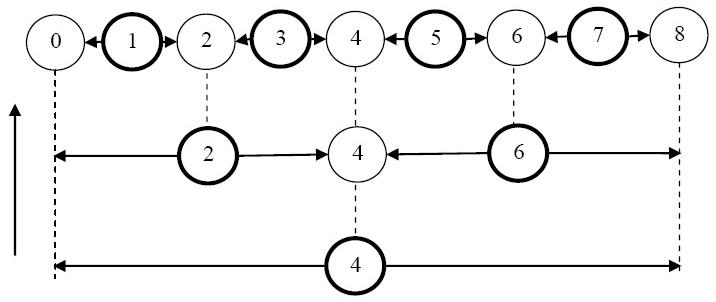
Для иллюстрации на рис. 3.14 приведена схема вычисления значений неизвестных при n=8. Согласно данной схеме переменные пересчитываются последовательно снизу вверх (пересчитываемые на каждом шаге переменные выделены, стрелками от них указаны переменные, значения которых используются при вычислении согласно формуле (7.39)).
Итак, прямой ход метода редукции состоит в вычислении по формулам (7.38) коэффициентов 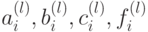 для
для 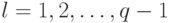 , а обратный ход состоит в нахождении решения по формуле (7.39) для
, а обратный ход состоит в нахождении решения по формуле (7.39) для 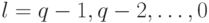
Общее число операций, требующееся для решения системы уравнений методом редукции, - 12n сложений, 8n умножений, 3n делений [5], т.е. метод является примерно таким же по трудоемкости, как и метод прогонки.
Параллельный алгоритм
Сформулируем теперь параллельный вариант метода редукции.
Анализ вычислительной схемы метода редукции показывает, что каждый последующий шаг прямого и обратного хода зависит от предыдущего. Зависимости по данным для этих операций на примере задачи при n=8 отражены на рис. 7.13 (прямой ход) и рис. 7.14 (обратный ход). Таким образом, распараллелить целиком прямой или обратный хода не получается.
С другой стороны, исключение неизвестных на отдельном шаге прямого хода можно проводить независимо, т.к. в этом случае зависимостей по данным нет. Аналогично может быть распараллелен отдельный шаг обратного хода, т.к. значения неизвестных находятся независимо.
Например, в задаче, проиллюстрированной на рис. 7.13 и рис. 7.14, на первом шаге прямого хода можно параллельно вычислить коэффициенты редуцированной системы уравнений относительно переменных 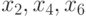 ; второй шаг прямого хода выполняется последовательно. А на первом шаге обратного хода можно параллельно вычислить значения переменных
; второй шаг прямого хода выполняется последовательно. А на первом шаге обратного хода можно параллельно вычислить значения переменных 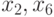 , а на втором шаге – значения
, а на втором шаге – значения 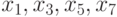 .
.
В заключение отметим, что при реализации рассмотренного параллельного алгоритма в системах с общей памятью не должен возникать эффект "гонки данных", связанный с доступом потоков к одинаковым областям памяти, т.к. распараллеливаемые отдельные шаги прямого и обратного хода не имеют зависимостей по данным.
Результаты вычислительных экспериментов
Для проведения вычислительных экспериментов выберем иную стратегию – многократное решение системы уравнений с одинаковой матрицей относительно небольшого размера и различными правыми частями (в отличие от предыдущего пункта, в котором решалась одна задача с матрицей большого размера). Решение указанной последовательности задач возникает, например, при численном решении дифференциальных уравнений в частных производных сеточными методами.
Вычислительные эксперименты для оценки эффективности метода редукции проводились на аппаратуре, технические характеристики которой указаны во введении. Для простоты написания параллельных программ нами рассматривались задачи размера, кратного степени двух, и решалась серия из 10 тыс. задач с одинаковой матрицей и разными правыми частями (подробная постановка данной задачи описана в лабораторной работе "Дифференциальные уравнения в частных производных"). Здесь же отметим лишь некоторую специфику данной серии задач. Матрица СЛАУ не зависит от номера задачи в серии, причем на диагонали расположены одинаковые числа, т.е. в системе (7.35)  ; а правая часть j-й задачи нелинейно зависит от решения (j-1)-й задачи (правая часть первой задачи в серии - известна).
; а правая часть j-й задачи нелинейно зависит от решения (j-1)-й задачи (правая часть первой задачи в серии - известна).
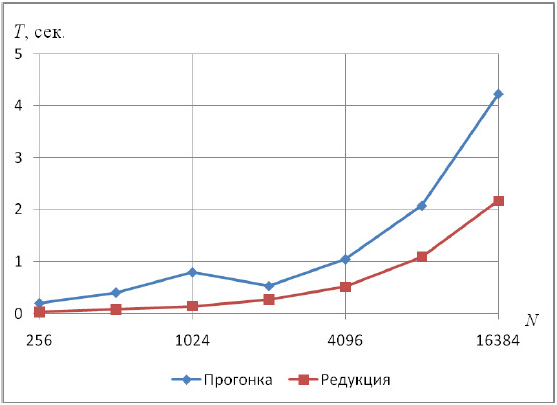
Теперь перейдем к результатам экспериментов. В табл. 3.10 приведено время решения серии из 10 тыс. задач c использованием методов прогонки и редукции на разных размерностях матрицы, а на рис. 7.15 показана зависимость времени решения от размерности матрицы СЛАУ.
| N | Время работы метода прогонки (сек) | Время работы метода редукции (сек) |
|---|---|---|
| 256 | 0,202 | 0,031 |
| 512 | 0,405 | 0,078 |
| 1024 | 0,795 | 0,14 |
| 2048 | 0,53 | 0,265 |
| 4096 | 1,045 | 0,514 |
| 8192 | 2,074 | 1,092 |
| 16384 | 4,227 | 2,169 |
| 32768 | 8,47 | 4,399 |
| 65536 | 19,11 | 9,111 |
Приведенные результаты показывают, что время решения задачи с помощью метода прогонки на всех размерностях матрицы более чем в 2 раза превышает время решения с использованием метода редукции, что противоречит теоретическим оценкам трудоемкости методов.
Полученный эффект можно объяснить существенным влиянием на результат архитектуры компьютера, на котором проводились эксперименты. В самом деле, если воспользоваться инструментами анализа производительности (напр., Intel Parallel Amplifier XE), можно увидеть, что в среднем операция метода прогонки выполняется почти за 2 такта, операция метода редукции - примерно за 1 такт. При этом количество инструкций в редукции приблизительно в 1.3 раза больше. Поскольку СЛАУ решается многократно, то время при использовании редукции меньше, чем при использовании метода прогонки. Подробное описание данного исследования приведено в лабораторной работе "Дифференциальные уравнения в частных производных".
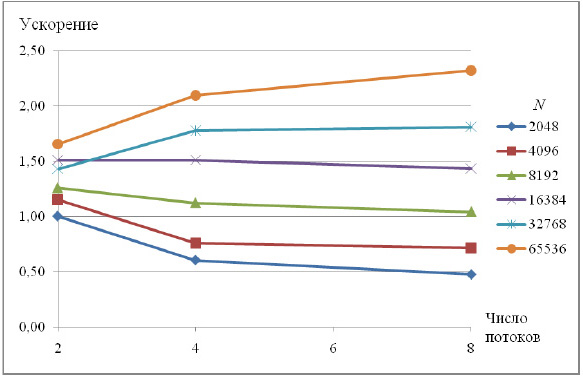
Теперь выполним анализ масштабируемости параллельной реализации метода циклической редукции. Ниже приведены показатели ускорения (относительной однопоточной реализации), соответствующие работе метода на 2, 4 и 8 потоках.
| N | 1 поток | Параллельный алгоритм | |||||
|---|---|---|---|---|---|---|---|
| 2 потока | 4 потока | 6 потоков | |||||
| T | T | S | T | S | T | S | |
| 2048 | 0,31 | 0,31 | 1,00 | 0,52 | 0,61 | 0,66 | 0,48 |
| 4096 | 0,59 | 0,51 | 1,15 | 0,78 | 0,76 | 0,83 | 0,72 |
| 8192 | 1,14 | 0,91 | 1,26 | 1,01 | 1,12 | 1,09 | 1,04 |
| 16384 | 2,22 | 1,47 | 1,51 | 1,47 | 1,51 | 1,55 | 1,43 |
| 32768 | 4,46 | 3,12 | 1,43 | 2,51 | 1,78 | 2,47 | 1,81 |
| 65536 | 9,19 | 5,55 | 1,65 | 4,38 | 2,10 | 3,96 | 2,32 |
Представленные результаты экспериментов свидетельствуют о плохой масштабируемости приложения, т.к. только при размерах задачи более 32 тыс. ускорение составляет немногим более двух в лучшем случае.
Данный факт можно объяснить тем, что распараллеливание выполнено на уровне внутреннего цикла прямого и обратного хода редукции, т.е. на каждой итерации редукции порождается или возобновляется несколько потоков, выполняется ожидание их завершения (фактически, точка синхронизации), после чего главный поток продолжает последовательные вычисления, т.е. значительную часть времени программа работает в 1 поток. Таким образом, значительное влияние на время работы программы оказывают накладные расходы, связанные с организацией параллелизма.
Если же посмотреть на параллельный метод редукции с точки зрения работы с данными, то можно сказать, что отсутствие масштабируемости также связано с неэффективной организацией работы с памятью. Пересчет правых частей СЛАУ и вычисление решения в методе осуществляется не последовательно, а с некоторым регулярным шагом на каждой итерации прямого и обратного хода редукции, это приводит к многочисленным кэшпромахам при увеличении числа потоков.
Таким образом, результаты экспериментов показывают, что решать системы с ленточной матрицей с использованием параллельных алгоритмов целесообразно лишь при достаточно большом размере матрицы, при этом в любом случае мы будем получать не очень значительное ускорение.