|
поддерживаю выше заданые вопросы
|
Математические основы параллельных вычислений
Цель лекции: Лекция направлена на знакомство слушателей математическими основами параллельных вычислений.
![]() Видеозапись лекции - (объем - 113 МБ).
Видеозапись лекции - (объем - 113 МБ).
Пользователь: почему?
Aijk = Ai-1jk + Bjk + Bjk, i=1,40; j=1,40; k=1,1000
Cray C90, пиковая производительность 960 Mflop/s
do k = 1, 1000
do j = 1, 40
do i = 1, 40
A(i,j,k) = A(i-1,j,k)+B(j,k)+B(j,k)
Производительность: 20 Mflop/s на Cray C90
Aijk = Ai-1jk + Bjk + Bjk, i=1,40; j=1,40; k=1,1000
Cray C90, пиковая производительность 960 Mflop/s
do i = 1, 40, 2
do j = 1, 40
do k = 1, 1000
A(i,j,k) = A(i-1,j,k)+2 ∗ B(j,k)
A(i+1,j,k) = A(i,j,k)+2 ∗ B(j,k)
Производительность: 700 Mflop/s на Cray C90
Умножение матриц: все ли просто?
| Фрагмент исходного текста: | Возможен ли порядок: |
for( i = 0; i < n; ++i)
for( j = 0; j < n; ++j)
for( k = 0; k < n; ++k)
A[i][j] = A[i][j] + B[i][k]∗C[k][j]
|
( i, k, j) - ?ДА |
| ( k, i, j) - ?ДА | |
| ( k, j, i) - ?ДА | |
| ( j, i, k) - ?ДА | |
| ( j, k, i) - ?ДА |
Порядок циклов: ( i, j, k)
(сравнение с порядком ( i, j, k) )
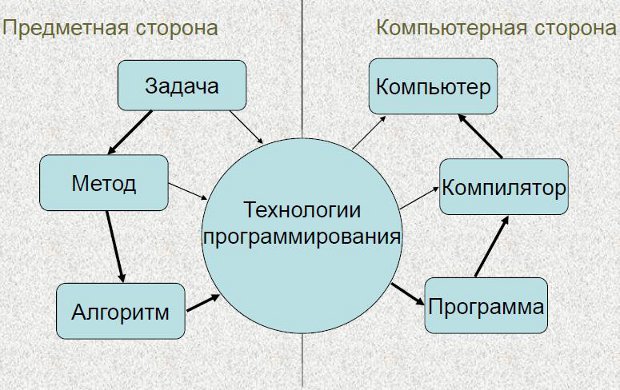
Решение задачи на компьютере
Графовые модели программ
Будем представлять программы с помощью графов: набор вершин и множество соединяющих их направленных дуг.
Вершины: процедуры, циклы, линейные участки, операторы, итерации циклов, срабатывания операторов…
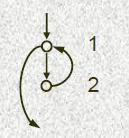
Вершины: итерации циклов.
for( i = 0; i < n; ++i) {
A[i] = A[i – 1] + 2;
B[i] = B[i] + A[i];
}
|
|
| Каждая вершина соответствует двум операторам (телу цикла), выполненным на одной и той же итерации цикла. |
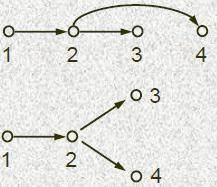
Вершины: срабатывания операторов.
for( i = 0; i < n; ++i) {
A[i] = A[i – 1] + 2;
B[i] = B[i] + A[i];
}
|
|
| Каждая вершина соответствует одному из двух операторов тела данного цикла, выполненному на некоторой итерации. |
Дуги: отражают связь (отношение) между вершинами.
Выделяют два типа отношений:
- операционное отношение,
- информационное отношение.
Дуги: операционное отношение:
Две вершины A и B соединяются направленной дугой тогда и только тогда, когда вершина B может быть выполнена сразу после вершины A.
Операционное отношение = отношение по передаче управления.
Дуги: информационное отношение:
Две вершины A и B соединяются направленной дугой B тогда и только тогда, когда вершина использует в качестве аргумента некоторое значение, полученное в вершине A.
Информационное отношение = отношение по передаче данных.
Четыре основные модели программ
Граф управления программы.
Вершины: операторы
Дуги: операционное отношение
Информационный граф программы.
Вершины: операторы
Дуги: информационное отношение
Операционная история программы.
Вершины: срабатывания операторов
Дуги: операционное отношение
Информационная история программы.
Вершины: срабатывания операторов
Дуги: информационное отношение