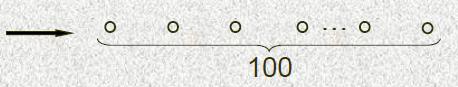|
поддерживаю выше заданые вопросы
|
Математические основы параллельных вычислений
Несколько вопросов…
Может ли информационная история некоторого фрагмента программы иметь 100 вершин и ни одной дуги?
ДА.
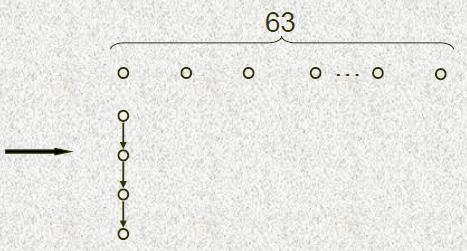
Может ли информационная история некоторого фрагмента программы иметь 67 вершин и 3 дуги?
ДА.
Может ли информационная история некоторого фрагмента программы иметь 20 вершин и 200 дуг?
НЕТ.
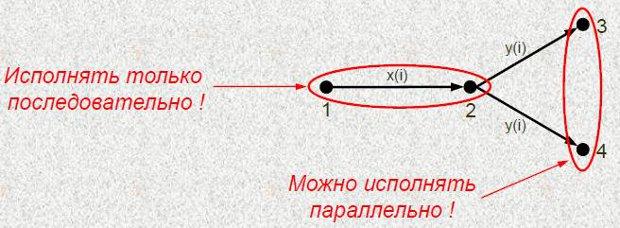
Модель некоторого фрагмента программы в качестве подграфа содержит следующий граф:
Какой моделью могла бы быть исходная модель?
Множество графовых моделей программ
Какое отношение выбрать для описания свойств программ?
Операционное отношение?
Информационная структура – это основа анализа свойств программ и алгоритмов.
x(i) = a + b(i) (1) y(i) = 2∗x(i) – 3 (2) t1 = y(i)∗ y(i) + 1 (3) t2 = b(i) – y(i)∗a (4)
Информационная зависимость определяет критерий эквивалентности преобразований программ.
Информационная независимость определяет ресурс параллелизма программы.
От компактных до историй: что выбрать для описания свойств программ?
Аргументы для выбора степени компактности модели:
- компактность описания,(компактные +)
- информативность,(истории +)
- сложность построения.(компактные +)
Граф алгоритма – это параметризованная информационная история:
- компактность описания за счет параметризации,
- имеет информативность истории,
- разработана методика построения графа
алгоритма по исходному тексту программ.
От компактных до историй: что выбрать для описания свойств программ?
Теорема о построении графа алгоритма
Теорема. Если фрагмент принадлежит к линейному
классу программ, то на основе статического анализа
можно построить компактное описание его графа
алгоритма в следующем виде: для каждого входа каждого оператора фрагмента
будет указано конечное множество троек вида 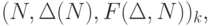 где:
где:  – линейный выпуклый многогранник в пространстве
внешних переменных фрагмента,
– линейный выпуклый многогранник в пространстве
внешних переменных фрагмента, 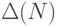 – линейный выпуклый многогранник в
пространстве итераций фрагмента,
– линейный выпуклый многогранник в
пространстве итераций фрагмента, 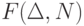 – линейная векторная функция, описывающая
входящие дуги оператора.
– линейная векторная функция, описывающая
входящие дуги оператора.
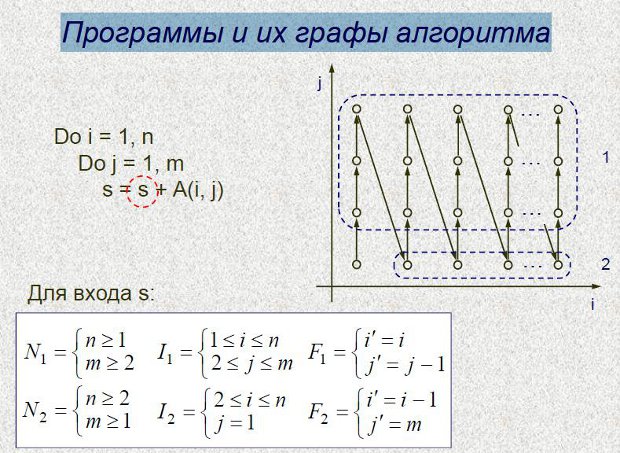
Программы и их графы алгоритма
(умножение матриц)