Умножение разреженных матриц

Метод вложенных сечений

Рассмотрим теперь еще один подход к получению переупорядочивания матрицы – метод вложенных сечений. Как и в предыдущем пункте, для описания метода нам потребуются некоторые дополнительные сведения из теории графов.

Расстоянием между вершинами графа 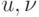называется длина кратчайшего пути, соединяющего эти вершины.

Наибольшее расстояние между любыми двумя вершинами графа называется диаметром графа.

Наибольшее расстояние от вершины u до любой другой вершины называется эксцентриситетом вершины и обозначается 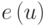. Таким образом,

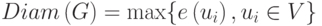
Если эксцентриситет вершины совпадает с диаметром графа, то такая вершина называется периферийной.

Псевдопериферийная вершина u определяется следующим условием: если 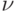– любая вершина, для которой выполнено условие 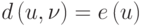, то будет выполнено и условие e\left(\nu\right)=e\left(u\right). Указанное определение гарантирует, что эксцентриситет псевдопериферийной вершины будет "близким" к диаметру графа.

Граф называется связным, если для каждой пары его вершин найдется путь, который их связывает. В противном случае граф называют несвязным. Всякий несвязный граф состоит из двух или более компонент связности.

Разделителем называется множество вершин, удаление которых вместе с инцидентными им ребрами приводит к появлению несвязного графа (или к увеличению числа связных компонент, если граф уже был несвязным). Разделитель называют минимальным, если никакое его собственное подмножество не является разделителем. Разделитель, состоящий из одной вершины, называется разрезающей вершиной.

Разбиением графа называется группировка вершин графа в попарно непересекающиеся подмножества 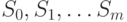. Если граф несвязный, и в качестве подмножеств выбраны его компоненты связности, то получаем разбиение на компоненты.

Одним из важных классов разбиений, использующихся при обработке разреженных матриц, является разбиение на уровни смежности, т.е. выявление структуры уровней смежности графа.

Структура уровней смежности 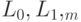, состоящая из m+1 уровня, получается, если указанные подмножества определены следующим образом:

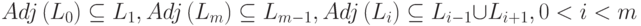( 7.46)

Напомним, что множество 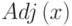для вершины 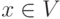является множеством смежных ей вершин. Число m называют длиной структуры уровней смежности, а ширина структуры определяется как максимальное количество вершин, составляющих каждый уровень.

Важным следствием из определения является тот факт, что в структуре уровней смежности каждый уровень 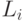, 0<i<m, является разделителем графа.

Разбиение на уровни смежности называют корневым с корнем 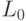, если , а каждое следующее множество смежно с объединением предыдущих, т.е.

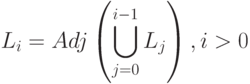( 7.47)

Если 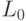состоит из единственной вершины u, то говорят, что структура уровней имеет корень в вершине u.

Рассмотрим теперь алгоритм построения структуры уровней смежности.

1. В графе V выбирается некоторая вершина 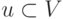в качестве корневой. Полагаем .
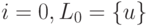2. Помечаем данную вершину (присваиваем ей первый номер)
3. Перебираем все вершины из множества 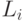, и для каждой его вершины определяем непомеченную смежную ей вершину. Эти смежные вершины образуют уровень 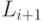. Они помечаются (нумеруются по порядку) и помещаются в .
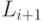4. Если множество непомеченных вершин пусто, то алгоритм завершен, иначе полагаем i=i+1, и переходим на шаг 3.

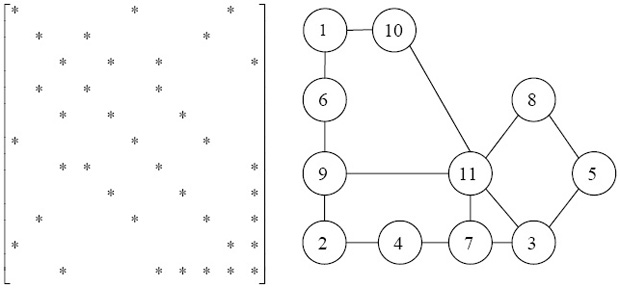
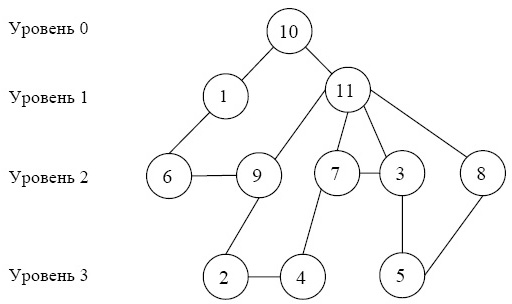
На рис. 7.35 приведена матрица разреженной системы линейных уравнений (ненулевые элементы отмечены символом *) и соответствующий ей граф, а на рис. 7.36 изображена структура уровней смежности для данного графа с корнем в вершине 10. Длина структуры равна 3, а ширина – 5. Отметим, что множество вершин {1, 11} первого уровня и множество вершин {6, 9, 7, 3, 8} второго уровня являются разделителями графа.

Рис. 7.35. Матрица и ее графовое представление

Рис. 7.36. Структура уровней смежности

В соответствии с книгами [9], [10] cформулируем алгоритм отыскания псевдопериферийной вершины r.

1. В графе V выбрать некоторую вершину 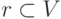в качестве корневой.
2. Определить структуру уровней смежности 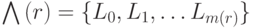с корнем в r.
3. Выбрать в последнем уровне вершину x с минимальной степенью.
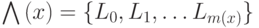4. Определить структуру уровней смежности с корнем в x.
5. Если 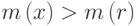, то положить 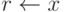, и перейти на шаг 3.
6. Узел x является псевдопериферийным.

После того, как введены все требуемые понятия и рассмотрены вспомогательные алгоритмы, сформулируем идею метода вложенных сечений.

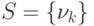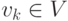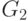Пусть исходной матрице A из (7.41) соответствует граф G(V,E). В графе G находим разделитель , где . Будем считать, что вершины в графе перенумерованы так, что удаление вершины (и инцидентных с ним ребер) приводит к появлению двух связных компонент и с вершинам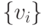и , , и , , соответственно. Так как 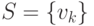является разделителем, то любая i-я вершина не будет достижима ни для какой j-й вершины из 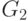. В этом случае все элементы фактора Холецкого 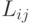с соответствующими номерами будут равны 0, и заполнения не произойдет.

Далее введем новую нумерацию вершин (которая соответствует перестановке переменных в системе уравнений): перенумеруем вершины в компонентах последовательно, от 1 до n–1 (для этого достаточно уменьшить номера вершин в компоненте 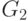, нумерация в останется прежней), а k-й вершине присвоим последний номер n, т.е. перенумеруем как .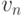

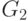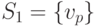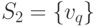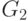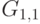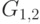Затем в каждой выделенной компоненте и проводим аналогичную процедуру: находим разделители в и в , выделяем четыре новые компоненты связности: и с вершинам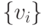и , , 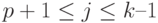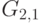и , ; и 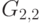с вершинам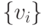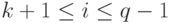и , , и , 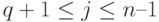. Следующий шаг алгоритма заключается в перенумерации вершин в пределах компонент указанным выше способом: вершины компонент связности нумеруются последовательно, разделителю присваивается последний номер. Если в какойлибо компоненте связности 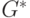нельзя найти разделитель, то в качестве соответствующего множества 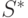выбирается само множество 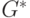и нумеруются все его вершины. Выполнение процедуры прекращается, если все компоненты связности исчерпаны.

При практической реализации алгоритма нумерацию можно организовать следующим образом: нумеровать все вершины разделителей S в обратном порядке (от n до 1), как только такое множество будет получено; вершины компонент связности G остаются непронумерованными. Окончательная нумерация вершин (т.е. матрица перестановки) определяется непосредственно после выполнения алгоритма.

Следует отметить, что разделитель S можно выбирать разными способами. Для того, чтобы метод вложенных сечений был максимально эффективным (т.е. в результате переупорядочивания возникали бы большие нулевые блоки в результирующем факторе L), следует придерживаться следующих правил:

• по возможности выбирать минимальный из всех разделителей (идеальный случай – разделитель из одной вершины):
• возникающие при удалении разделителя компоненты связности должны быть примерно одинакового размера.

Известный метод выбора подходящего разделителя, описанный в [9], состоит в построении для графа структуры уровней смежности с корнем в псевдопериферийной вершине и выборе малого разделителя из "среднего" уровня.

Дадим формальное описание метода вложенных сечений. Пусть 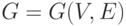– граф, ассоциированный с матрицей A. Тогда метод вложенных сечений будет состоять в следующем.

1. Положить R=V, n=\left|V\right|.
2. Найти в G(R) связную компоненту G(C) и построить для нее структуру уровней смежности с корнем в псевдопериферийной вершине r, т.е. .
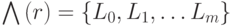3. Если , то положить S=С и перейти к шагу 4. В противном случае положить и определить разделитель S как множество узлов 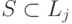такое, что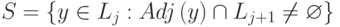
4. Перенумеровать узлы разделителя S числами от n до 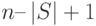. Положить 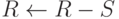и 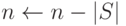. Если , то перейти на шаг 2.

На шаге 3 алгоритма разделитель S можно получить простым отбрасыванием тех узлов из 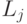, которые не смежны ни с одним узлом из .

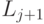Подробное изучение свойств рассмотренных нами алгоритмов может быть найдено в книгах [9],[10].

Результаты экспериментов

Для иллюстрации мы вернемся к разложению рассмотренных в п.3.5.3.2 матриц из коллекции http://www.cise.ufl.edu/research/sparse/matrices/. Также как и в прошлый раз, сравним коэффициент заполнения исходной матрицы A, фактора L, полученного "в лоб", и фактора 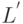, полученного после применения перестановки, найденной методом вложенных сечений (см. таблицу и рисунки ниже). Для сравнения приведен коэффициент заполнения факт 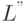, полученного после применения перестановки, найденной методом минимальной степени.

Таблица 7.13. Коэффициенты заполнения матрицы до и после разложения

Матрица	A	L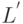
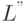shallow_water2	4,88281E-05	0,00687	0,00065	0,00075
pwtk	0,00024268	0,00803	0,00281	0,00256
parabolic_fem	1,32902E-05	0,16134	0,00019	0,00017
cfd2	0,000202489	0,02049	0,02048	0,00877

Для наглядности приведем портреты матриц, переупорядоченных методом вложенных сечений.

Рис. 7.37. Матрица shallow_water2, n=81 920, nz=204 800

Рис. 7.38. Матрица parabolic_fem, n=525 825, nz=2 100 225

Рис. 7.39. Матрица pwtk, n=217 918, nz=5 871 175

Рис. 7.40. Матрица cfd2, n=123 440, nz=1 604 423

Рис. 7.41. Фактор для shallow_water2, n=81 920, nz=2 183 332

Рис. 7.42. Фактор для parabolic_fem, n=525 825, nz=26 494 693

Рис. 7.43. Фактор для pwtk, n=217 918, nz=66 843 598

Рис. 7.44. Фактор для cfd2, n=123 440, nz=156 075 674

Эксперименты показывают, что метод вложенных сечений в целом дает примерно такие же коэффициенты заполнения, что и метод минимальной степени. Значительное отличие есть только для матрицы cfd2, которое объясняется ее особой структурой – элементы матрицы расположены близко к главной диагонали (см. портрет матрицы на рис. 7.24), поэтому перестановка не дает столь значительных (по сравнению с другими примерами) результатов.